----------------------------------------------------------------------------------------
Name O R A 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
----------------------------------------------------------------------------------------
Z1 1 0 + 1 - - - - - - - - - - - - - -
Z2 2 1 + 1 1 - - - - - - - - - - - - -
Z3 3 1 + 1 - 2 - - - - - - - - - - - -
Z4 4 1 + 1 1 - 2 - - - - - - - - - - -
K4 4 2 + 1 3 - 0 - - - - - - - - - - -
Z5 5 1 + 1 - - - 4 - - - - - - - - - -
D6 6 2 - 1 3 2 - - 0 - - - - - - - - -
Z6 6 1 + 1 1 2 - - 2 - - - - - - - - -
Z7 7 1 + 1 - - - - - 6 - - - - - - - -
Z8 8 1 + 1 1 - 2 - - - 4 - - - - - - -
Z4 x Z2 8 2 + 1 3 - 4 - - - 0 - - - - - - -
D8 8 2 - 1 5 - 2 - - - 0 - - - - - - -
Q8 8 2 - 1 1 - 6 - - - 0 - - - - - - -
Z3^3 8 3 + 1 7 - 0 - - - 0 - - - - - - -
Z9 9 1 + 1 - 2 - - - - - 6 - - - - - -
Z3^2 9 2 + 1 - 8 - - - - - 0 - - - - - -
D10 10 2 - 1 5 - - 4 - - - - 0 - - - - -
Z10 10 1 + 1 1 - - 4 - - - - 4 - - - - -
Z11 11 1 + 1 - - - - - - - - - 10 - - - -
Q12 12 2 - 1 1 2 6 - 2 - - - - - 0 - - -
Z12 12 1 + 1 1 2 2 - 2 - - - - - 4 - - -
A4 12 2 - 1 3 8 0 - 0 - - - - - 0 - - -
D12 12 2 - 1 7 2 0 - 2 - - - - - 0 - - -
Z6 x Z2 12 2 + 1 3 2 0 - 6 - - - - - 0 - - -
Z13 13 1 + 1 - - - - - - - - - - - 12 - -
D14 14 2 - 1 7 - - - - 6 - - - - - - 0 -
Z14 14 1 + 1 1 - - - - 6 - - - - - - 6 -
Z15 15 1 + 1 - 2 - 4 - - - - - - - - - 8
----------------------------------------------------------------------------------------
Name O R A 1 2 4 8 16
Z16 16 1 + 1 1 2 4 8
Z4^2 16 2 + 1 3 12 - -
K4 # Z4 16 2 - 1 7 8 - -
Z4 # Z4 16 2 - 1 3 12 - -
Z8 x Z2 16 2 + 1 3 4 8 -
Z8 #5 Z2 16 2 - 1 3 4 8 -
D16 16 2 - 1 9 2 4 -
Z8 #3 Z2 16 2 - 1 5 6 4 -
Q16 16 2 - 1 1 10 4 -
Z4 x K4 16 3 + 1 7 8 - -
D8 x Z2 16 3 - 1 11 4 - -
Q8 x Z2 16 3 - 1 3 12 - -
Pauli 16 3 - 1 7 8 - -
Z2^4 16 4 + 1 15 - - -
------------------------------------------------
Name O R A 1 17
Z17 17 1 + 1 16
----------------------------------------------------
Name O R A 1 2 3 6 9 18
D18 18 2 - 1 9 2 - 6 -
Z18 18 1 + 1 1 2 2 6 6
D6 x Z3 18 2 - 1 3 8 6 - -
Z3 # D6 18 3 - 1 9 8 - - -
Z6 x Z3 18 2 + 1 1 8 8 - -
----------------------------------------------------
Name O R A 1 19
Z19 19 1 + 1 18
----------------------------------------------------
Name O R A 1 2 3 4 9 20
Q20 20 2 - 1 1 10 4 4 -
Z20 20 1 + 1 1 2 4 4 8
Z5 # Z4 20 2 - 1 5 10 4 - -
D20 20 2 - 1 11 - 4 4 -
Z10 x Z2 20 2 + 1 3 - 4 12 -
----------------------------------------------------
Name O R A 1 3 7 21
Z7 # Z3 21 2 - 1 14 6 -
Z21 21 1 + 1 2 6 12
----------------------------------------------------
Name O R A 1 2 11 22
D22 22 2 - 1 11 10 -
Z22 22 1 + 1 1 10 10
----------------------------------------------------
Name O R A 1 23
Z23 23 1 + 1 22
------------------------------------------------------------
Name O R A 1 2 3 4 6 8 12 24
Z3 # Z8 24 2 - 1 1 2 2 2 12 4 -
Z24 24 1 + 1 1 2 2 2 4 4 8
2T 24 2 - 1 1 8 6 8 - - -
Q24 24 2 - 1 1 2 14 2 - 4 -
D6 x Z4 24 2 - 1 7 2 8 2 - 4 -
D24 24 2 - 1 13 2 2 2 - 4 -
Q12 x Z2 24 2 - 1 3 2 12 6 - - -
8G24 24 2 - 1 9 2 6 6 - - -
Z12 x Z2 24 2 + 1 3 2 4 6 - 8 -
D8 x Z3 24 2 - 1 5 2 2 10 - 4 -
Q8 x Z3 24 2 - 1 1 2 6 2 - 12 -
S4 24 2 - 1 9 8 6 - - - -
A4 x Z2 24 2 - 1 7 8 - 8 - - -
D12 x Z2 24 3 - 1 15 2 - 6 - - -
Z6 x K4 24 3 + 1 7 2 - 14 - - -
------------------------------------------------------------
Name O R A 1 5 25
Z25 25 1 + 1 4 20
Z5^2 25 2 + 1 24 -
--------------------------------------------
Name O R A 1 2 13 26
D26 26 2 - 1 13 12 -
Z26 26 1 + 1 1 12 12
--------------------------------------------
Name O R A 1 3 9 27
Z27 27 1 + 1 2 6 18
Z9 x Z3 27 2 + 1 8 18 -
Z3^2 # Z3 27 2 - 1 26 - -
Z9 # Z3 27 2 - 1 8 18 -
Z3^3 27 3 + 1 26 - -
------------------------------------------------------------
Name O R A 1 2 3 6 13 28
Q28 28 2 - 1 1 14 6 6 -
Z28 28 1 + 1 1 2 6 6 12
D28 28 2 - 1 15 - 6 6 -
Z14 x Z2 28 2 + 1 3 - 6 18 -
------------------------------------------------------------
Name O R A 1 29
Z29 29 1 + 1 28
------------------------------------------------------------
Name O R A 1 2 3 5 6 10 15 30
D6 x Z5 30 2 - 1 3 2 4 12 - 8 -
D10 x Z3 30 2 - 1 5 2 4 10 - 8 -
D30 30 2 - 1 15 2 4 - - 8 -
Z30 30 1 + 1 1 2 4 2 4 8 8
------------------------------------------------------------
Name O R A 1 31
Z31 31 1 + 1 30
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Name O R A 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
----------------------------------------------------------------
Name O R A 1 2 3 4 6 9 12 18 36
Q36 36 2 - 1 1 2 18 2 6 - 6 -
Z36 36 1 + 1 1 2 2 2 6 4 - 12
K4 # Z9 36 2 - 1 3 2 0 6 24 - - -
D36 36 2 - 1 19 2 0 2 6 - 6 -
Z18 x Z2 36 2 + 1 3 2 0 6 6 - 18 -
Q12 x Z3 36 2 - 1 1 8 6 8 - 12 - -
Z3 # Q12 36 3 - 1 1 8 18 8 - - - -
Z12 x Z3 36 2 + 1 1 8 2 8 - 16 - -
Z3^2 # Z4 36 2 - 1 9 8 18 0 - - - -
D6^2 36 2 - 1 15 8 0 12 - - - -
A4 x Z3 36 2 - 1 3 26 0 6 - - - -
D6 x Z6 36 2 - 1 7 8 0 20 - - - -
Z6 # D6 36 3 - 1 19 8 0 8 - - - -
Z6^2 36 2 + 1 3 8 0 24 - - - -
----------------------------------------------------------------
Name O R A 1 2 4 5 8 10 20 40
Z5 #4 Z8 40 2 - 1 1 2 4 20 4 8 -
Z40 40 1 + 1 1 2 4 4 4 8 16
Z5 #2 Z8 40 2 - 1 1 10 4 20 4 - -
Q40 40 2 - 1 1 22 4 - 4 8 -
D10 x Z4 40 2 - 1 11 12 4 - 4 8 -
D40 40 2 - 1 21 2 4 - 4 8 -
Q20 x Z2 40 2 - 1 3 20 4 - 12 - -
K4 # D10 40 2 - 1 13 10 4 - 12 - -
Z20 x Z2 40 2 + 1 3 4 4 - 10 16 -
D8 x Z5 40 2 - 1 5 2 4 - 20 8 -
Q8 x Z5 40 2 - 1 1 6 4 - 4 24 -
D10 # Z4 40 2 - 1 11 20 4 - 4 - -
D20 x Z2 40 3 - 1 23 - 4 - 12 - -
Z10 x K4 40 3 + 1 7 - 4 - 28 - -
------------------------------------------------------------
Name O R A 1 41
Z41 41 1 + 1 40
------------------------------------------------------------
Name O R A 1 2 3 6 7 14 21 42
Z7 #3 Z6 42 2 - 1 7 14 14 6 - - -
Z7 #4 Z6 42 2 - 1 1 14 14 6 6 - -
D6 x Z7 42 2 - 1 3 2 - 6 18 12 -
D14 x Z3 42 2 - 1 7 2 14 6 - 12 -
D42 42 2 - 1 21 2 - 6 - 12 -
Z42 42 1 + 1 1 2 2 6 6 12 12
------------------------------------------------------------
Name O R A 1 2 5 10 25 50
D50 50 2 - 1 25 4 - 20 -
Z50 50 1 + 1 1 4 4 20 20
D10 x Z5 50 2 - 1 5 24 20 - -
Z5^2 # Z2 50 3 - 1 25 24 - - -
Z10 x Z5 50 2 + 1 1 24 24 - -
----------------------------------------------------
Name O R A 1 2 4 13 26 52
Q52 52 2 - 1 1 26 12 12 -
Z52 52 1 + 1 1 2 12 12 24
Z13 # Z4 52 2 - 1 13 26 12 - -
D52 52 2 - 1 27 - 12 12 -
Z26 x Z2 52 2 + 1 3 - 12 36 -
------------------------------------------------------------
Name O R A 1 2 3 6 9 18 27 54
D54 54 2 - 1 27 2 - 6 - 18 -
Z54 54 1 + 1 1 2 2 6 6 18 18
D18 x Z3 54 2 - 1 9 8 18 18 - - -
D6 x Z18 54 2 - 1 3 8 6 18 18 - -
5G54 54 2 - 1 9 26 18 - - - -
Z9 #2 Z6 54 2 - 1 9 8 18 18 - - -
7G54 54 3 - 1 27 8 - 18 - - -
8G54 54 3 - 1 9 26 18 - - - -
Z9 x Z6 54 2 + 1 1 8 8 18 18 - -
10G54 54 2 - 1 1 26 26 - - - -
Z18 # Z3 54 2 - 1 1 8 8 18 18 - -
D6 x Z3^2 54 2 - 1 3 26 24 - - - -
13G54 54 3 - 1 9 26 18 - - - -
14G54 54 4 - 1 27 26 - - - - -
Z6 x Z3^2 54 3 - 1 1 26 26 - - - -
------------------------------------------------------------
Name O R A 1 3 7 9 21 63
Z7 # Z9 63 2 - 1 2 6 42 12 -
Z63 63 1 + 1 2 6 6 12 36
Z7 # Z3^2 63 2 - 1 44 6 - 12 -
Z21 x Z3 63 2 + 1 8 6 - 21 -
----------------------------------------------------
Name O R A 1 3 5 15 25 75
Z75 75 1 + 1 2 4 8 20 40
Z5^2 # Z3 75 2 - 1 50 24 - - -
Z15 x Z5 75 2 + 1 2 24 48 - -
----------------------------------------------------

 и группа
и группа  имеют одинаковый "вектор порядков элементов": 1-3-4-8-0 (для порядков 1-2-4-8-16). Так же они имеют одинаковый ранк, и единственным их глобальным отличием является то, что одна из них абелева, а другая — нет. Аналогичная ситуация с группами 27-го порядка
имеют одинаковый "вектор порядков элементов": 1-3-4-8-0 (для порядков 1-2-4-8-16). Так же они имеют одинаковый ранк, и единственным их глобальным отличием является то, что одна из них абелева, а другая — нет. Аналогичная ситуация с группами 27-го порядка  и
и  , они имеют одинаковый вектор 1-8-18-0 (для порядков 1-3-9-27), одинаковый ранк и отличаются только абелевостью.
, они имеют одинаковый вектор 1-8-18-0 (для порядков 1-3-9-27), одинаковый ранк и отличаются только абелевостью.

![$$=\left\langle\;a,\;b\;|\;a^3=b^3=c^3=d^2=[a,\;b]=[a,\;c]=[b,\;c]=[c,\;d]=(ad)^2=(bd)^2=I\;\right\rangle$$ $$=\left\langle\;a,\;b\;|\;a^3=b^3=c^3=d^2=[a,\;b]=[a,\;c]=[b,\;c]=[c,\;d]=(ad)^2=(bd)^2=I\;\right\rangle$$](https://dxdy-01.korotkov.co.uk/f/8/9/a/89a62f6986853e638a2917c89943121c82.png) Обе они имеют ранк 3, их "вектор порядков" 1-9-26-18-0-0-0-0 (для порядков 1-2-3-6-9-18-27-54), и обе они не абелевы. Единственное отличие сразу бросающееся в глаза (и легко считающееся, что не мало важно), — вторая имеет нетривиальный центр.
Обе они имеют ранк 3, их "вектор порядков" 1-9-26-18-0-0-0-0 (для порядков 1-2-3-6-9-18-27-54), и обе они не абелевы. Единственное отличие сразу бросающееся в глаза (и легко считающееся, что не мало важно), — вторая имеет нетривиальный центр. .
.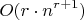 где
где  . А ранг - это наименьшая мощность порождающего множества. Мне в голову приходит только перебор всех подмножеств порядка
. А ранг - это наименьшая мощность порождающего множества. Мне в голову приходит только перебор всех подмножеств порядка  .
. -группы класса 2 и экспоненты
-группы класса 2 и экспоненты  . Там все нетривиальные элементы порядка
. Там все нетривиальные элементы порядка  Но я такой не знаю.
Но я такой не знаю. Да, заставляет задуматься.
Да, заставляет задуматься.![$[G, G] \leq \mathrm C(G)$ $[G, G] \leq \mathrm C(G)$](https://dxdy-03.korotkov.co.uk/f/e/e/c/eecf9e7f6308418be74c6d0385e8be7182.png) , и так далее.
, и так далее. и
и  .
. получается решётка с векторами:
получается решётка с векторами:


