Нужна консультация об ошибках/”дырах"/надуманных заявлениях

Лукомор · 22/07/08 1416 Предместья

transcendent в сообщении #1637818 писал(а):

Уважаемый Лукомор, откуда Вы взяли, что этот пример
был взят для того, чтобы я получал это

А я просто не понимаю, как из
$m=a+b$
и $n=c$ можно найти $a$ и $b$

-- Чт май 02, 2024 17:54:07 --

transcendent в сообщении #1637818 писал(а):

пока все принимающие здесь участие не приняли факт, что m и n могут быть не только ЦЕЛЫМИ числами,

Они по определению - натуральные.
Какие еще иррациональные числа во времена Пифагора, и тем более - Евклида?

transcendent · 26/01/24 64

Лукомор в сообщении #1637822 писал(а):

А я просто не понимаю, как из
$m=a+b$
и $n=c$ можно найти $a$ и $b$

- ещё раЗ: я и не пытался показать Вам и/или иным читателям форума

Лукомор в сообщении #1637822 писал(а):

как из
$m=a+b$
и $n=c$ можно найти $a$ и $b$

конкретно в примере

transcendent в сообщении #1637805 писал(а):

Покажите, пожалуйста, хотя бы, здесь ошибку: transcendent в сообщении #1637780
писал(а):
$m=3/(2^{1/2})$ , (33), $n=1/(2^{1/2})$ , (34). Проверяем: $A=(3/(2^{1/2}))^2-(1/(2^{1/2}))^2=9/2-1/2=8/2=4$ , $B=2\cdot (3/(2^{1/2}))\cdot (1/(2^{1/2}))=2\cdot 3/2=3$ , $C=(3/(2^{1/2}))^2+(1/(2^{1/2}))^2=9/2+1/2=10/2=5$ .

-Этот пример был представлен только для демонстрации факта нецелых (иррациональных в данном случае) m и n.....несмотря на то, что,

Лукомор в сообщении #1637822 писал(а):

Они по определению - натуральные.

,-у меня они не натуральные,- и что

Лукомор в сообщении #1637822 писал(а):

Какие еще иррациональные числа во времена Пифагора, и тем более - Евклида?

.
То, о чём Вы спрашиваете, было показано на стр.1, правда, я бы сказал, в противоположном порядке:

transcendent в сообщении #1637141 писал(а):

Действительно, только Пифагоровы Тройки дают целые числа для уравнений, типа, (15), как например, для Пифагоровой Тройки 3, 4, 5, имея $m=3+4=7$ , (17), $n=(3^2+4^2)^{1/2}=5$ , (18), катет B будет целым: $B=7\cdot5=35$ , (19). Любые целые числа x и y, не составляющие какую-то Пифагорову Тройку, не будут давать целые числа для катетов B, как и для числа n, (20), даже при $p=2$ , (21).

. Конечно, можно сделать и то, что вы просите, т.е. написать в том порядке, в котором Вы спрашиваете, но зачем, если это и так видно, что это возможно?...Я же показывал Вам "фокус" с другой Пифагоровой Тройкой, которая была выбрана именно Вами: 5, 12, 13.
Если что-то непоянтно, может, Вы как-то напишете , типа, в личку или ещё как? А то я боюсь, что меня сейчас выгонят к псам сейчас-я уже написал выше, ведь:

mihaild в сообщении #1637819 писал(а):

я постараюсь минимизировать мои комментарии здесь.

И что мне теперь делать? Надеюсь, Вы специально такую цель не ставите, чтоб меня выгнали...
Уважаемый mihaild, я ж писал, что понял Вас.

mihaild в сообщении #1637819 писал(а):

Ну так задайте его. Так, чтобы его можно было понять.

Лукомор · 22/07/08 1416 Предместья

transcendent в сообщении #1637823 писал(а):

я и не пытался показать Вам и/или иным читателям форума

А вы попытайтесь!
Когда мы смотрим на формулы Евклида для генерации пифагоровых троек,
мы там ясно видим, как из всех без исключений пар натуральных чисел $m$ и $n$ получаются все без исключения пифагоровы тройки:
$a=m^2-n^2$
$b=2mn$
$c=m^2+n^2$
Но мы так же ясно видим и обратное, как из пифагоровой тройки получить эти самые $m$ и $n$ :
$m=\sqrt{\frac{z+x}{2}}= \frac{\sqrt{z+y}+\sqrt{z-y}}{2}$
$n=\sqrt{\frac{z-x}{2}}= \frac{\sqrt{z+y}-\sqrt{z-y}}{2}$
В ваших преобразованиях обратного хода я не вижу, и как из ваших:
$m=x+y$ , $n=z$ получить обратно эту же пифагорову тройку, мне непонятно.

transcendent · 26/01/24 64

Лукомор в сообщении #1637848 писал(а):

я и не пытался показать Вам и/или иным читателям форума

- эта цитата вырвана из моего сообщения

Лукомор в сообщении #1637848 писал(а):

transcendent в сообщении #1637823
писал(а):

- вырвана ИЗ КОНТЕКСТА, как говорится. Речь шла о конкретном примере, который обсуждался вчера. Об этом примере:

transcendent в сообщении #1637823 писал(а):

Покажите, пожалуйста, хотя бы, здесь ошибку: transcendent в сообщении #1637780
писал(а):
$m=3/(2^{1/2})$ , (33), $n=1/(2^{1/2})$ , (34). Проверяем: $A=(3/(2^{1/2}))^2-(1/(2^{1/2}))^2=9/2-1/2=8/2=4$ , $B=2\cdot (3/(2^{1/2}))\cdot (1/(2^{1/2}))=2\cdot 3/2=3$ , $C=(3/(2^{1/2}))^2+(1/(2^{1/2}))^2=9/2+1/2=10/2=5$ .

-к нему я не показал в деталях, то, что Вы спрашиваете. А показал только конечные результаты -иррациональные значения m и n , полученные из заданной Пифагоровой Тройки 4,3,5 по формулам Эвклида при $Epsilon=1$ -если я помню точно.... То, что Вы сейчас спрашиваете, было УЖЕ показано в моём комментарии 26.04.2024, 20.30 мск, в ответ на Ваше пожелание "продемонстировать тот же ловкий фокус с Пифагоровой Тройкой 5, 12, 13":

transcendent в сообщении #1637388 писал(а):

Лукомор в сообщении #1637384
писал(а):
Возьмите пифагоровую тройку $(5, 12, 13)$ ,
и продемонстрируйте нам тот же ловкий фокус, который Вы проделали с тройкой
$3, 4, 5$ в первом сообщении...

Я Вам дал ответ и копирую его снова, сюда же:

transcendent в сообщении #1637388 писал(а):

-правильно ли я понял Вас, что Вы хотели сказать именно то, что я должен взять Пифагорову Тройку $x=5$ , $y=12$ , $z=13$ и написать уравнения $m=5+12=17$ и $n=z=(5^2+12^2)^{1/2}=(25+144)^{1/2}=13$ , чтобы потом показать следующую Пифагорову тройку, которая сконструировна из заданной Вами исходной Пифагоровой Тройки? Т.е., мы получили m=17, n=13. Ну,отсюда же легко всё найти, учитывая , что полученные m и n есть оба нечётные. Следовательно, $Epsilon=1/2$ и мы имеем для следующей Пифагоровой Тройки, X,Y,Z: $X=Epsilon\cdot(m^{2}-n^{2})=(1/2)\cdot(17^{2}-13^{2})=60$ , $Y=Epsilon\cdotmn=17\cdot13=221$ , $Z=Epsilon\cdot(m^{2}+n^{2})=(1/2)\cdot(17^{2}+13^{2})=229$ . Т.е., мы получили новую Пифагорову Тройку $X=60$ , $Y=221$ , $Z=229$ . Проверка-элементарна. Этот вопрос почему-то насторожил меня, не подвох ли какой?.. Что тут Вам не нравится? Ах, возможно, я не правильно понял Ваш вопрос и слово "фокус"? Это уже не моя вина, ведь, мы знаем, что в математике, если что-то не написано, то этого не существует, не так ли?:) Но, хорошо, думаю дальше. Возможно, Вы хотели, чтоб я пошёл не "вверх", а "вниз"? Т.е., Вы хотели бы, чтобы я к указанной Вами Пифагоровой Тройки 5, 12, 13 нашёл m и n и именно для этих m и n "спустился" "вниз"? Хорошо, давайте попробуем. Обозначим m и n указанной Вами Пифагоровой Тройки индексом "middle" , рассчитывая их стандартно. Мы нашли, что $m_{middle}=5$ и $n_{middle}=1$ . Действительно, $y=Epsilon\cdot(5^{2}-1^{2})=(1/2)\cdot(25-1)=12$ , $x=2\cdot(Epsilon)\cdot5\cdot1=5$ , $z=Epsilon\cdot(5^{2}+1^{2})=(1/2)\cdot(25+1)=13$ -"Ваша" Пифагорова тройка получена, следовательно, m и n найдены правильно и мы работаем с ними дальше, чтобы найти m и n с индексом "previous". Стандартный метод расчёта даёт следующие значения искомых величин, одно из которых есть иррациональное число: $m_{previous}=2.449490...$ , $n_{previous}=2$ .
Элементарная проверка по ФЭ даёт значения $m_{middle}=(1/2)\cdot(2.449490...^{2}+2^{2})=(1/2)\cdot10=5$ и $n_{middle}=(1/2)\cdot(2.449490...^{2}-2^{2})=(1/2)\cdot2=1$ , Q.E.D.
Правильно я всё сделал?

-Я использовал формулы Эвклида при $Epsilon=1/2$ тоже.
Вы не ответили на это. Ни тогда (26.04.2024), ни вчера. Во всяком случае, я не вижу комментария на этот мой ответ от 26.04.2024, 20.30., -может я что-то упустил?
Вы сейчас показали формулы Эвклида для $Epsilon=1$ -зачем? Ведь, именно эти ФЭ были использованы для этого примера:

transcendent в сообщении #1637823 писал(а):

Покажите, пожалуйста, хотя бы, здесь ошибку: transcendent в сообщении #1637780
писал(а):
$m=3/(2^{1/2})$ , (33), $n=1/(2^{1/2})$ , (34). Проверяем: $A=(3/(2^{1/2}))^2-(1/(2^{1/2}))^2=9/2-1/2=8/2=4$ , $B=2\cdot (3/(2^{1/2}))\cdot (1/(2^{1/2}))=2\cdot 3/2=3$ , $C=(3/(2^{1/2}))^2+(1/(2^{1/2}))^2=9/2+1/2=10/2=5$ .

. Что такое "обратный ход" в этом Вашем вопросе-

Лукомор в сообщении #1637848 писал(а):

В ваших преобразованиях обратного хода я не вижу, и как из ваших:
$m=x+y$ , $n=z$ получить обратно эту же Пифагорову Тройку, мне непонятно.

-Видимо, вы хотите спросить как были получены $m=3/(2^{1/2})$ и $т=1/(2^{1/2})$ ?
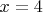
Тогда, отвечаю-как обычно, по тем же ФЭ, которые Вы сейчас показали, при $Epsilon=1$ (Вы почему-то это не указали): Для Пифгоровой Тройки $x=4$ , $y=3$ , $z=5$ мы пишем $m=((1/2)\cdot(z+x))^{1/2}=((1/2)\cdot(5+4))^{1/2}=(9/2)^{1/2}=3/(2^{1/2})$ , $n=((1/2)\cdot(z-x))^{1/2}=((1/2)\cdot(5-4))^{1/2}=(1/2)^{1/2}=1/(2^{1/2})$ . Вот и всё. Не понял-что здесь не понятно? Если я помню хорошо-проверку я показывал? Сейчас гляну...Да, вот она:

transcendent в сообщении #1637798 писал(а):

transcendent в сообщении #1637780
писал(а):
$m=3/(2^{1/2})$ , (33), $n=1/(2^{1/2})$ , (34). Проверяем: $A=(3/(2^{1/2}))^2-(1/(2^{1/2}))^2=9/2-1/2=8/2=4$ , $B=2\cdot (3/(2^{1/2}))\cdot (1/(2^{1/2}))=2\cdot 3/2=3$ , $C=(3/(2^{1/2}))^2+(1/(2^{1/2}))^2=9/2+1/2=10/2=5$ .

Хорошо, если уже я сегодня уже зашёл на форум, давайте "спустимся ещё ниже", т.е., обозначим только что найденные выше значения m и n индексом "middle" и найдём "нижележащие" m и n , которые обозначим индексом "previous", пользуясь теми же самыми ФЭ при $Epsilon=1$ . Т.е., "нижележащие" $m_{previos}$ и $n_{previos}$ будут задавать нам $m_{middle}$ и $n_{middle}$ , которые, в свою очередь, определяют нам Пифагорову Тройку 4,3,5. Мы находим, что $m_{previous}=2^{1/4}$ и $n_{previous}=1/(2^{1/4})=2^{-1/4}$ .
Проверка: $m_{middle}=m_{previous}^2+n_{previous}^2=(2^{1/4})^2+(2^{-1/4})^2=3/(2^{1/2})$ и $n_{middle}=m_{previous}^2-n_{previous}^2=(2^{1/4})^2-(2^{-1/4})^2=1/(2^{1/2})$ -результаты совпадают с найденынми выше значениями для $m_{middle}=3/(2^{1/2})$ и $n_{middle}=1/(2^{1/2})$ .
Т.е., я Вам продемонстировал (ещё раз) "обратный ход" не только от Пифагоровой Тройки 4, 3, 5 (о таких мы вчера тоже упоминали, что это не одно и то же, что 3,4,5), но и ещё "ниже".
Я предвижу, что у Вас возникнет законный вопрос-"как ты нашёл/нашла $m_{previous}$ и $n_{previous}$ "? Отвечаю: пока в общем виде показано, как конечный результат, без детализации. Но, всё это сделано не выходя за рамки "Эвклида" и "Пифагора" (исключая требование о целых числах, естественно-для меня...), причём не "зацикливаясь", что имеющиеся зависимости/уравнения/законы релевантны только Пифагоровым Тройкам...Детали, возможно,позже обсуждать...Не сейчас.
Почему Вы пренебрегаете моими просьбами, просьбами, высказанными неоднократно выше?

transcendent в сообщении #1637823 писал(а):

я постараюсь минимизировать мои комментарии здесь.

Почему Вы пренебрегаете моими опасениями? Я ни разу не проявил к Вам какого-то неуважения. Ведь, так, Лукомор ?
Что сейчас есть такого "горящего", что не терпит появления от меня отредактированной версии моих сомнений относительности правомерности применения метода от противного для доказательства ВТФ?
По-моему, "небо на Землю не падает и Дунай в своём течении не остановился".
Если же Вы хотите искренне что-то прояснить, то пусть бы кто-то дал гарантию, что данная переписка здесь безопасна для моего аккаунта с точки зрения получения бана за частые сообщения. Или с точки зрения удаления данной дискуссии. Пока таких гарантий нет, я постараюсь придерживаться этого:

transcendent в сообщении #1637823 писал(а):

я постараюсь минимизировать мои комментарии здесь.

Лукомор · 22/07/08 1416 Предместья

transcendent в сообщении #1637855 писал(а):

Речь шла о конкретном примере, который обсуждался вчера

Меня не интересуют конкретные примеры...

-- Пт май 03, 2024 15:16:13 --

transcendent в сообщении #1637855 писал(а):

Я использовал формулы Эвклида при $Epsilon=1/2$ тоже.

к Евклиду претензий не имею, с Эвклидом не знаком.
А теперь используйте ваши формулы.

-- Пт май 03, 2024 15:19:05 --

transcendent в сообщении #1637855 писал(а):

Что сейчас есть такого "горящего", что не терпит появления от меня отредактированной версии моих сомнений относительности правомерности применения метода от противного для доказательства ВТФ?

Меня не интересует ваше, или любое другое,
доказатльство ВТФ.
Давайте разберемся с вашими наездами на Евклида и Пифагора, и на этом закончим...

-- Пт май 03, 2024 15:19:14 --

transcendent · 26/01/24 64

Лукомор в сообщении #1637879 писал(а):

А теперь используйте ваши формулы.

-"Использовать"-где? Что Вас не устроило в моём предыдущем комментарии?

Лукомор в сообщении #1637879 писал(а):

Давайте разберемся с вашими наездами на Евклида и Пифагора, и на этом закончим...

-Слово "наезды" не определено. Если Вы имеете в виду что-то "бытовое", Вы ошибаетесь. Какие могут быть "наезды"... И-да, давайте "закончим".

Уважаемые Админы, уважаемый Заслуженный Участник mihaild , уважаемый Супермодератор Ende -кто здесь командует. Пожалуйста, закройте эту ветку и/или делайте с ней всё, что вам/Вам угодно. Я не хотел бы далее общаться в таком режиме, который мне навязывает уважаемый Лукомор. Он не смотрит на мои ответы. +Словечки из 90-ых -ЭТО ЧТО?....Никому ничего не интересно, все пишущие считают, что всё неправильно, gibberish и т.д., объясняя тем, что читать нет смысла. Что ж, нет смысла-так нет смысла. Более того, с самого начала были же призывы от одного из уважаемых Заслуженных участников прикрыть это всё. Почему ж им не последовать?... Всё. Нет смысла. [Однако, не думайте, что я не имею что сказать. Впрочем, и по этому вопросу всё всем "до лампочки". Правда, "Шурик"?]
Всего всем наилучшего.

П.С. Нащщщот "Е" или "Э":
1. "Э" и "Е": http://hrono.ru/biograf/bio_ye/evklid.php
2. Больше "Э", чем "Е": https://eponym.ru/Search/Person/862
3. "Е" и "Э": https://ru.wikipedia.org/wiki/%D0%95%D0 ... 0%B8%D0%B4
4. Только "Э": https://ru.wiktionary.org/wiki/%D0%AD%D ... 0%B8%D0%B4
Суперские претензии, Шурик. Суперские. Также забираю все мои "спасибо" и "извинения" в Ваш адрес.
Всего вам доброго.

Лукомор · 22/07/08 1416 Предместья

transcendent в сообщении #1637881 писал(а):

Использовать"-где? Что Вас не устроило в моём предыдущем комментарии?

Использовать ваши формулы там, где вы прикрылсь формулами Евклида...

-- Пт май 03, 2024 16:41:52 --

transcendent в сообщении #1637881 писал(а):

И-да, давайте "закончим".

Конечно, но сначала разберемся со спиленным вами деревом пифагоровых троек...

-- Пт май 03, 2024 16:48:08 --

transcendent в сообщении #1637881 писал(а):

Я не хотел бы далее общаться в таком режиме, который мне навязывает уважаемый Лукомор. Он не смотрит на мои ответы.

Я никому ничего не навязывал...
Более того, я не видел ни одного ответа по существу ваших преобразований, хотя они и не ваши. Это все есть в википедии, и в статьях известных математиков, в известных журналах, которые (статьи) мне лень искать в сети, и не интересно читать, потому что это все страшно далеко от моих теперешних интересов...

Я искренне пытался вам помочь, но вам не нужна помощь...
До свидания!

-- Пт май 03, 2024 16:48:13 --

transcendent · 26/01/24 64