- это верно.
снова неправильный, в десять раз отличается от верного.
Вы писали вроде бы, что с помощью преподавателя освоили Delphi. Я совсем не программист, но предполагаю, что на Delphi и вообще на любом из существующих теперь компьютерных языков "высокого уровня" при желании всегда можно выполнить интересующее вычисление.
Когда я был студентом, в 1970-х, нас научили всё считать на логарифмических линейках. Этот сильно устаревший способ не буду здесь описывать.
Позднее, в 1980-х, у нас в лабораториях появились первые настольные ЭВМ (Электронные Вычислительные Машины - так в то время назывались компьютеры). Им в оперативную память можно было загружать с магнитофонных кассет версию языка "Бейсик" - очень простую и поэтому удобную даже для тех людей, кто совсем не знал программирования.
Тот Бейсик я освоил, и даже теперь иногда им пользуюсь в симуляторе старинной ЭВМ. Вот так выглядит алгоритм и результат расчёта величин

и

прямо по приведённым Вами числам:
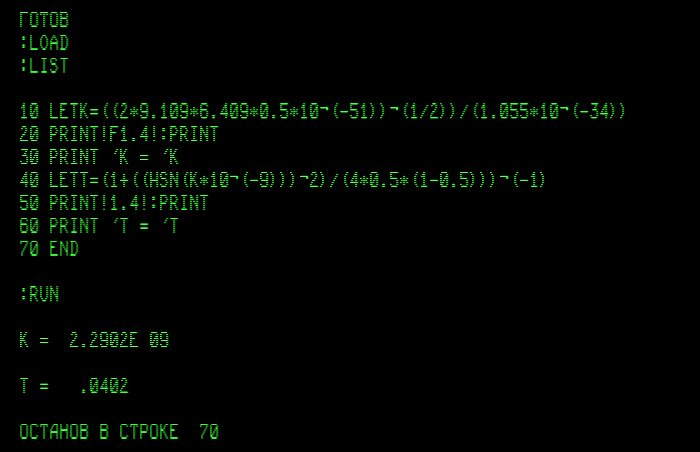
Бейсик несложный: оператор LET означает присваивание значения переменной, указанной сразу за этим словом; оператор PRINT!F1.4! задаёт формат печати чисел - одна цифра до и четыре цифры после плавающей десятичной точки; двоеточие разделяет операторы в строке, если их в одной строке несколько; PRINT просто выводит на экран пустую строку для красоты, а если есть текст в апострофах и буквенное имя переменной, то на экран выводится этот текст и значение переменной; функция sinh(x) обозначена как HSN(X); знак возведения в степень похож на "кочергу", остальные математические знаки выглядят более-менее привычно. Строки выполняются в порядке возрастания их нумерации (и по командам переходов в них, если такие команды есть).
Зная это, Вы легко переведёте бейсиковскую запись алгоритма на любой доступный Вам язык программирования.
Однако, желательно программировать не одноразовый расчёт по фиксированным входным данным, а более универсальный расчёт - в котором пользователь мог бы сам вводить входные данные, и тем самым варьировать их, чтобы затем анализировать, как изменяется результат.
При этом целесообразно сначала вычислить характерные для конкретной задачи условные "единицы" величин, и затем входные данные выражать через безразмерные количества таких "единиц". Например, за условную единицу энергии можем выбрать

где

- масса электрона,

энергия

приблизительно равна

Тогда безразмерное произведение

для частицы с массой

энергией

и барьера

длиной

запишется в виде:

С немножко другими обозначениями вот листинг такого типа бейсик-программки (годится для перевода на любой доступный Вам язык программирования):

Вот так этот расчёт работает с прежними входными данными (разумеется, получается и тем самым проверяется прежний результат):
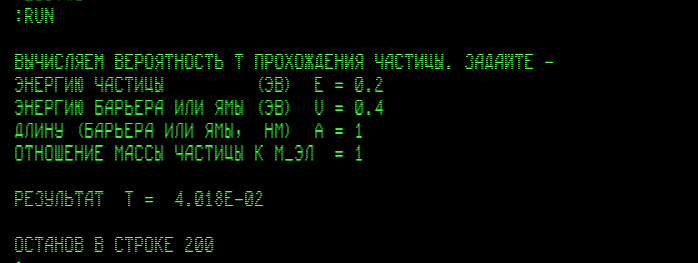
Посмотрим, например, как при прочих прежних условиях уменьшится вероятность туннелирования в случае частицы, которая в 2000 раз массивнее электрона, т.е. у которой масса примерно такая же, как масса ядра легчайшего атома:
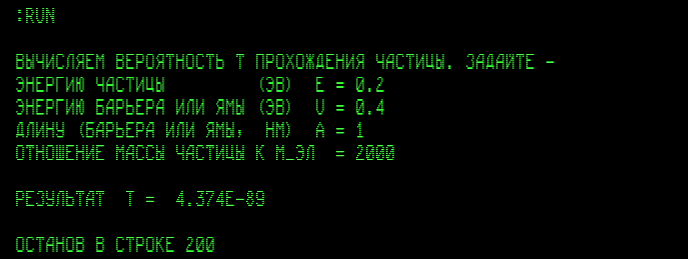
Получилось приблизительно

эта запись означает

Ещё один давно известный удобный способ учебных студенческих расчётов - в программе "Маткад", работающей под управлением Windows. Это не бесплатная программа. Есть у неё и недостатки, а удобна она тем, что формулы в ней записываются почти в таком же привычном виде, как в учебниках по математике и физике; кроме того, в ней есть встроенная "помощь" с примерами - это обучающий материал. Описание её есть и в интернете. Для наших примеров Маткад даёт те же результаты, которые указаны выше. Подробнее на этом не останавливаюсь.
Есть также возможность делать программируемые расчёты даже на тех компьютерах, где не установлены никакие специальные программы, кроме интернет-браузера. Например, у меня в браузере Firefox (устаревшая версия под управлением устаревшей Windows 7 на устаревшем ноутбуке, да и сам-то я уже старик) нормально работает самодельный html-код, который легко пишется в простейшем текстовом редакторе - в "Блокноте". Сам бы я до такого дела не догадался; спасибо моим бывшим студентам: они научили меня этому способу лет 20 тому назад. С тех пор я иногда этим способом пользуюсь, отыскивая небходимые подсказки в интернете.
Ещё раз подчеркну: у меня нет программистких знаний. Поэтому предупреждаю: я не знаю, будет ли такой код выполняться в других браузерах и на других компьютерах, притом с выводом на экран слов на русском языке, в обычной кодировке windows-1251. Но на форуме есть знатоки программирования, и может быть, они подскажут, что и как отредактировать в коде типа приводимого ниже для его работоспособности на современном компьютере.
Вот этот код; если его скопировать отсюда в текстовый файл, сохранить в своём компьютере как файл типа html, и запустить на исполнение в браузере, то, предположительно, он выполнит простой расчёт

и

по вашим исходным числам:
Код:
<HTML>
<HEAD>
<meta http-equiv="Content-Type" content="text/html; charset=windows-1251">
<TITLE>Вычисление Т</TITLE>
</HEAD>
<BODY>
<H3> Вычисляем вероятность туннелирования T </H3>
<FORM name = "calc">
<P>Дано: барьер U = 0.4 эВ, a = 1 нм, m = масса электрона, E/U = 0.5.<BR>
<P>Нажмите кнопку
<input name = "btnCalc" type = "button" value = "Вычислить K·a и T"
onClick = "
var K = Math.sqrt((2*9.109*6.409*0.5*1e-51))/(1.055*1e-34)
var Ka = K*1e-9
var Sh = Math.sinh(Ka)
var T = 1.0/(1+Math.pow(Sh,2)/(4*0.5*(1-0.5)))
var out_Ka = Math.trunc(Ka*10000+0.5)/10000
var out_T = Math.trunc(T*10000+0.5)/10000
calc.result_1.value = out_Ka
calc.result_2.value = out_T
" ><BR>
<P><B>Результат</B>:
<BR><BR>
K·a = <input type = "text" size = 10 name = "result_1">
T = <input type = "text" size = 10 name = "result_2"> <BR>
</FORM>
</BODY>
</HTML>
Вот так выглядит экран с результатом работы этой программки:

А вот упоминавшаяся выше (в терминах языка "Бейсик") программка на языке html с более универсальным расчётом:
Код:
<HTML>
<HEAD>
<meta http-equiv="Content-Type" content="text/html; charset=windows-1251">
<TITLE>Вычисление Т</TITLE>
<script language="JavaScript">
function calcT(E, U, a, m)
{
if(E<0)
{E=-E}
if(m<0)
{m=0}
var Eta = E/U
var E1 = Math.pow(1.055,2)/(2*9.109*1.6022e-2)
var a1 = a/0.1
var U1 = U*m*Math.pow(a1,2)/E1
if(E>U)
{
var Ka = Math.sqrt(U1*(Eta-1))
var S = Math.sin(Ka)
Result = 1/(1+Math.pow(S,2)/(4*Eta*(Eta-1)))
}
else
{
var Ka = Math.sqrt(U1*(1-Eta))
var S = Math.sinh(Ka)
Result = 1/(1+Math.pow(S,2)/(4*Eta*(1-Eta)))
}
return Result
}
</script>
</HEAD>
<BODY>
<H3> Вычисляем вероятность T прохождения частицы за барьер или за яму</H3>
<FORM name = "calc">
<P><B>Задайте</B>:<BR>
энергию частицы E>0 (эВ), <BR>
энергию барьера или ямы U (эВ) и длину a>0 (нм), <BR>
отношение массы m частицы к массе электрона<BR><BR>
Е (зВ) = <input type = "text" size = 20 name = "arg1"><BR>
U (эВ) = <input type = "text" size = 20 name = "arg2"><BR>
a (нм) = <input type = "text" size = 20 name = "arg3"><BR>
m/m_эл = <input type = "text" size = 20 name = "arg4"><BR>
<P>И нажмите кнопку
<input name = "btnCalc" type = "button" value = "Вычислить T"
onClick = "
var E = 1.0*calc.arg1.value
var U = 1.0*calc.arg2.value
var a = 1.0*calc.arg3.value
var m = 1.0*calc.arg4.value
var T = calcT(E,U,a,m)
var out_T = Math.trunc(T*10000+0.5)/10000
calc.result_1.value = out_T
calc.result_2.value = T
" ><BR>
<P><B>Результат</B>:
<BR>
<P>значение, округленное до 4 цифр после десятичной точки:<BR>
T = <input type = "text" size = 30 name = "result_1"> <BR>
<P>неокругленное значение:<BR>
T = <input type = "text" size = 30 name = "result_2"> <BR>
</FORM>
</BODY>
</HTML>
Вот скриншот с результатом для ваших первоначальных данных:

и вот для случая с частицей в 2000 раз более массивной, чем электрон, при прежних прочих условиях:

Видно, что результаты расчёта на Бейсике и в html-программках согласуются друг с другом; этот факт служит здесь проверкой машинного результата. А надо сказать, что проверка вычислений является одним из основных этапов в процессе вычислений. Этап проверок иногда занимает львиную долю всего времени расчётов.
Машинный счёт дело хорошее, однако надо всегда стремиться заранее оценить хотя бы порядок (десятичный) интересующих величин. Мы знаем (так как раньше уже вычисляли), что характерная энергия
Т.е. в данном примере величина
раз. Поэтому прежний результат
Вот мы и проверили машинные ответы. Заодно из этой оценки видно, что вероятность туннелирования резко убывает с ростом массы частицы. Понятно также, что она резко убывает и с увеличением длины барьера
- ведь эти величины тоже входят в выражение для показателя экспоненты: чем они больше, тем показатель экспоненты
больше.



