Вопросы по математическим основам квантовой механики

[Cos(x-pi/2)]

Решил я привести-таки конкретный пример результатов расчёта движения и туннелирования волнового пакета, выполненного по указанной в предыдущем сообщении схеме. Ну, просто на всякий случай; вдруг, начинающим изучать азы КМ будет интересно взглянуть.

Волновая функция в упоминавшейся задаче с потенциальным барьером, имеющимся при $0<x<a,$ рассчитывалась численно (с некоторыми приближениями, но в нюансы сейчас не вдаюсь) на промежутке $-18\cdot a<x<18\cdot a.$

Длина барьера $a$ выбрана в расчёте за единицу длины; величина $\hbar /a$ выбрана за единицу импульса, так что $1/a$ - единица волнового вектора; величина $\frac{\hbar^2}{2ma^2}$ служит единицей энергии; $\frac{ma^2}{\hbar}$ - единица времени: это время классического пролёта единицы длины со скоростью, соответствующей единице импульса.

В этих единицах высота потенциального барьера $U_0$ (на шкале энергии) и значения параметров начальной волновой функции для формул, указанных в предыдущем сообщении, были для примера выбраны так: $U_0=6,$ центр распределения $a(q)$ волнового вектора: $q_0=2,$ параметр ширины этого распределения: $d=0.25.$

Считается, что источник посылает частицы к барьеру слева направо, в состоянии нормированного волнового пакета. Значению $q_0=2$ соответствует скорость движения волнового пакета, равная двум единицам. Причём, к моменту времени $t=0$ центр пакета прибыл бы в точку $x=0,$ если бы этому не препятствовал потенциальный барьер.

Значит, в момент времени $t=-7$ центр движущегося направо пакета находится ещё только в точке $x=-14.$ Вот с этого момента и сделаны дальнейшие расчёты положения и формы волнового пакета с шагом по времени в 2 единицы, т.е. в 4 единицы по расстоянию вдоль оси $x.$ Вот картинки (правда, не знаю, как долго они просуществуют; раньше не пользовался этим хостингом изображений, а того, которым я ещё совсем недавно пользовался, уже нет):

(Графики движущегося и туннелирующего волнового пакета)

Ниже на всех рисунках область с барьером выделена серым цветом.

Вот так выглядит квадрат модуля волновой функции, имеющей вид волнового пакета, - решения нестационарного у. Ш. в задаче с потенциальным барьером $U(x),$ - в тот момент времени, когда волновой пакет ещё только появляется в левой стороне промежутка $-18<x<18:$




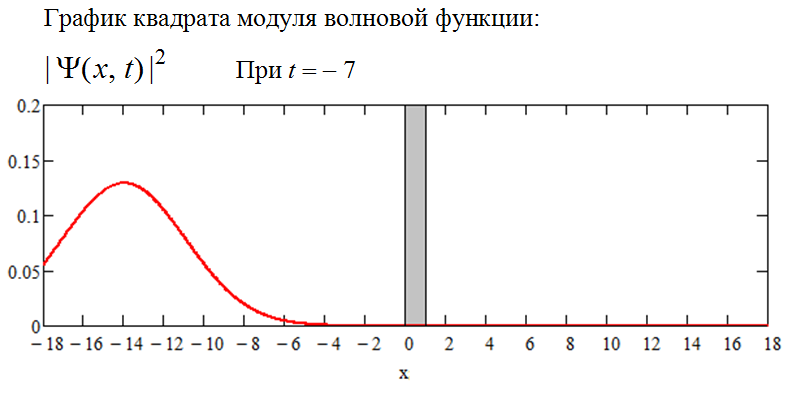
Через две единицы времени пакет продвинулся направо на четыре единицы длины:




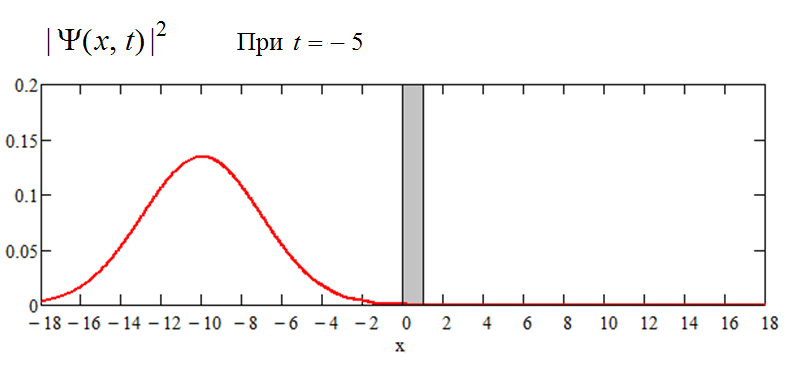
Еще через две единицы времени пакет уже приблизился к барьеру и начал отражаться назад - на графике проявились первые признаки интерференции движущихся к барьеру и отражающихся от барьера волн, имеющихся в составе пакета:




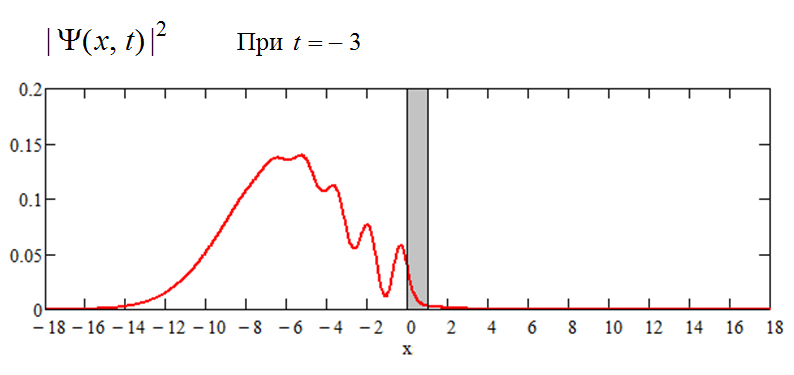
Пакет пытается пройти через барьер, но большей частью отражается назад: интерференция видна уже "в полный рост". Пакет по-прежнему нормирован, т.е. площадь под этим графиком равна единице (приближённо в приближённом расчёте). Поскольку появились минимумы, а нормировка сохранилась прежняя, то увеличились значения квадрата модуля волновой функции в максимумах интерференционной картины; чтобы график полностью поместился, масштаб по вертикали здесь (и на следующем графике) изменён в два раза:




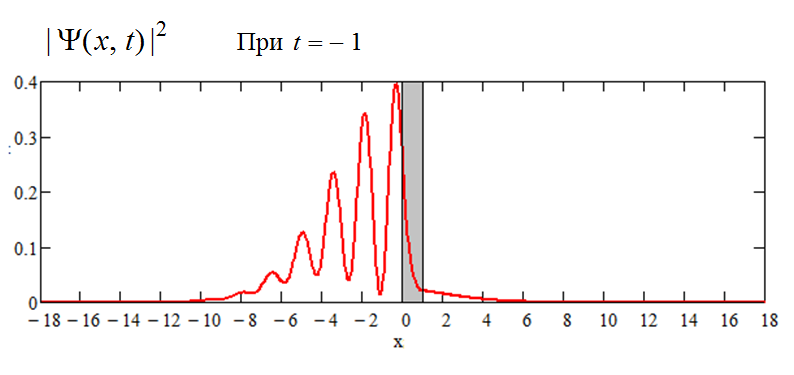
Продолжается отражение пакета от барьера; лишь малая часть проникла направо за барьер:




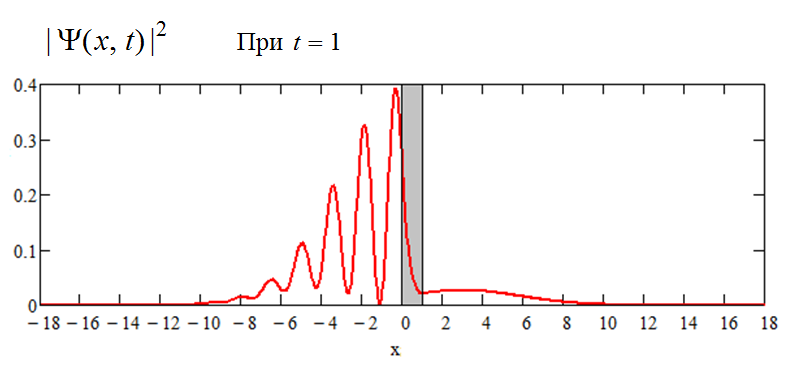
Отразившаяся часть пакета удаляется от барьера назад, налево, а проникшая сквозь барьер часть - направо; интерференция становится менее заметной, масштаб по вертикали восстановлен первоначальный:




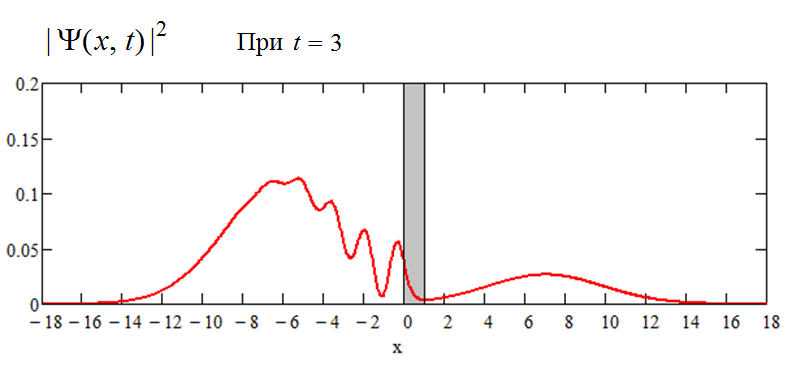
Обе части продолжают двигаться в противоположных направлениях по разные стороны барьера, как два самостоятельных волновых пакета:




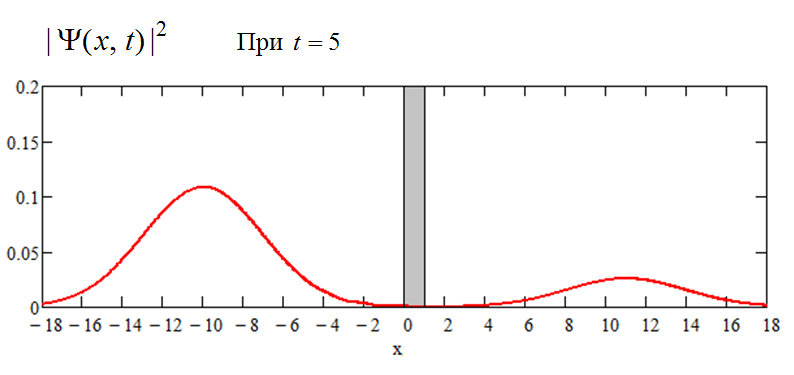
И так далее:




---------------------

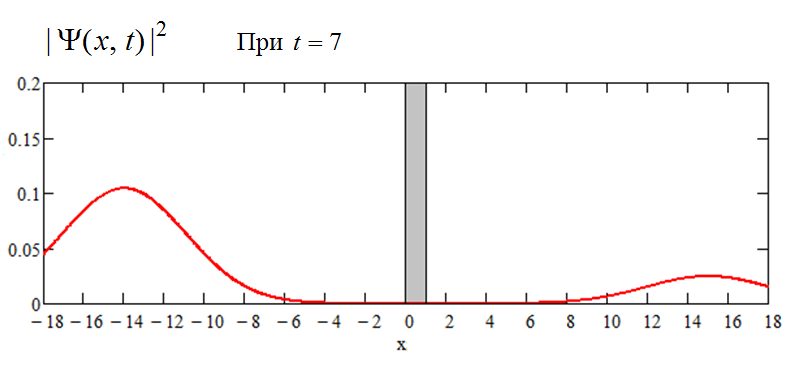
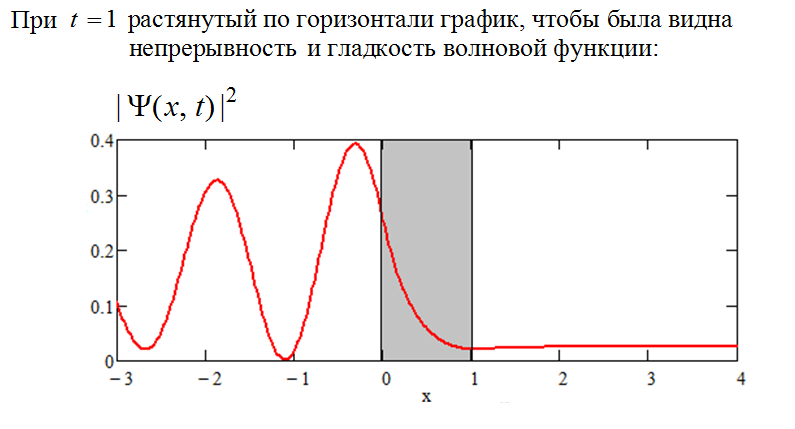
Приведу ещё один рисунок - растянутый по горизонтали график для момента времени $t=1,$ когда пакет находился в области барьера. Здесь видно, что "сшивание" значений волновой функции, а также значений её производной, на границах барьера не испортилось - разрывов и изломов у графика нет:




--------------------


После того, как отразившийся налево и прошедший за барьер направо пакеты удалились друг от друга (перестали перекрываться на оси $x),$ можно вычислить вероятность отражения частицы как интеграл по $x$ от отразившегося пакета - это площадь под его графиком.

И, аналогично, вероятность прохождения за барьер, т.е. вероятность туннелирования, - это площадь под графиком пакета, движущегося направо справа от барьера.

В данном конкретном примере ответы получились вот такие (в сумме единица, как и должно быть для вероятностей):

вероятность отражения: 0.808155
вероятность прохождения: 0.191845

Те же самые значения, 0.808155 и 0.191845, в этом примере получаются также просто как квадраты модуля амплитуд отражённой волны и прошедшей волны, имеющих определённый волновой вектор: $-q_0$ и $q_0$ соответственно. Амплитуды определяются только упоминавшимися условиями "сшивания", без рассмотрения волновых пакетов. Таким образом, когда требуется лишь найти вероятности отражения и прохождения, а картина динамики во времени нестационарной волновой функции нас не интересует, то и нет необходимости выполнять громоздкие расчёты волновых пакетов.

[pppppppo_98]

Уважаемый! Я таки сильно удивлен, когда прочел что вы читаете, учебник по квантовой химии. Отложите вы его на время. Для того что бы его читать и понимать, надо основы знать, а вы операций с комплексными числами не знаете. А квантовая химия меж тем это сложнейшая прикладная область квантовой механик, и там точно нужно знать досконально в объеме 3 тома (а иногда и 4 тома) весь Ландавшиц... Спуститесь на 2 уровня ниже прочтите сначала первые пару глав ТФКП (не надо даже лезть в вычеты - все равно вы сами интегралы брать никогда не будите), прочтите хотя бы ускоренно уравнения дифференциальные уравнения (хотя бы линейные), и уравнения математической физики (хотя бы что бы знать что такое оператор, собственный значения, что такое вариационное исчисление, что такое обощенные функции , и как с ними работать). Ужо потом можно браться за третий том Книги бытия(не лучшее изложение, но зато хороший справочник и все в принципе есть) вместе с задачником Галицкого, а уж затем в квантовую химию лезть... Да еще бы неплохо бы и статистическую механику почитать, ибо часто и густо используется (квантовая) статистическая механика при расчете всяких макроскопических величин, типа константы скоростей.

Да и если вы думаете что, молекулярная динамика взята с потолка и является классической, то я вас глубоко разочарую - молекулярная динамика появиляется из молекулярной квантовой электродинамики (это отдельное приложение квантовой электродинамики), из которой выбрасывают в конце рассмотрения все квантовые корреляции переходя к плотностям вероятности, и эффективным потенциалам , ибо рассматривают взаимодействие на относительно удаленных масштабах.

----
Вы случаем не программист, который рекрутировался в фирму занимающейся химическим расчетами? Мне как-то сильно удивительно как с такими багажом вас занесло в квантовую химию. А в институтах прежде, чем давать квантовую химию обычно проходят сопуствующие спецкурсы, хотя бы в начальном объеме.

ЗЗЫ
Галицкого настоятельно рекомендую скачать. и прорешать несколько первых глав... Или хотя бы просмотреть решения... Э

[pppppppo_98]

читаю вот аннотацию той книги, что и вы читаете

цитирую

Книга рассчитана на студентов/аспирантов химических и физических факультетов, освоивших математический анализ, линейную алгебру и дифференциальные уравнения.

[B3LYP]

Cos(x-pi/2)

Да, понял:

$|e^{ix}|^2=(e^{ix})^{*}(e^{ix})=(\cos(x)-i \sin(x))(\cos(x)+i \sin(x))=\cos^2(x)-i^2 \sin^2(x)=\cos^2(x)+\sin^2(x)=1$

$P= \int_{-\infty}^{\infty}((Ce^{-ikx})^*(-i \hbar) \frac{d(Ce^{-ikx})}{dx}dx)= \int_{-\infty}^{\infty}((Ce^{-ikx})^*(-i \hbar) (-ik Ce^{-ikx})dx)= -\hbar C^2 k \int_{-\infty}^{\infty}((e^{-ikx})^* e^{-ikx}dx)$=-\hbar C^2 k |_{-\infty}^{\infty}(x)

Правильно?

Cos(x-pi/2) в сообщении #1622664 писал(а):

Перемножить две экспоненты, имеющие противоположные показатели, наверное, сумеете.

Вы имеете в виду, что если сопрячь экспоненту от мнимого числа, то это равноценно смена знака у множителя к i в экспоненте?

Cos(x-pi/2) в сообщении #1622664 писал(а):

Вот пояснения на случай, если со всеми своими затруднениями справитесь и продолжите борьбу. Дальнейший разбор вопроса о том, как в КМ можно описывать движение частицы с заданной скоростью, сводится к рассмотрению волновой функции в форме того или иного "волнового пакета".

Я пока не очень понял ваш текст, давайте вернусь к нему немного позже. Пока только вопрос

Cos(x-pi/2) в сообщении #1622664 писал(а):

$$\Psi(x,t)=\int \limits_{-\infty}^{\infty} a(q)\, e^{iqx-i\frac{E(q)}{\hbar}t}\,\frac{dq}{2\pi}.$$

Функция $a(q)$ подчиняется условию нормировки, чтобы обеспечивалась нормированность волновой функции $\Psi(x,t)$

$$\int \limits_{-\infty}^{\infty} |a(q)|^2\,\frac{dq}{2\pi}=1.$$

Волновой пакет, или, как его ещё называют, "группа волн" с близкими значениями волнового вектора $q \approx q_0$ получается с функцией $a(q),$ имеющей максимум при заданном значении $q_0$ в центре заданного интервала $\Delta q,$ и быстро убывающей вне этого интервала.

Почему вы пишете $a(q)$, а не $\Psi(x)$?

Cos(x-pi/2) в сообщении #1622664 писал(а):

(P.S. И, между прочим, я не понимаю, почему Вы только гуглите и видео смотрите, а высококачественные учебники в формате pdf или djvu не читаете. Не тот гаджет? Без чтения книг по математике и физике ничего хорошего не получится. "Любите книгу - источник знаний" (c))

Мне трудно изучать такие предметы по учебникам. Раньше не мог выучить Delphi и ООП по книгам, а потом пошёл на платные курсы и преподаватель мне на пальцах всё объяснил. В то же время если я понял что-то сложное, мне кажется у меня хорошо получается понятно это объяснять.
Пока мне удобен такой формат как сейчас - на форуме отвечают на мои вопросы, а я всех развлекаю флеймовыми темами в других разделах...

[пианист]

B3LYP в сообщении #1623100 писал(а):

$|e^{ix}|^2=(e^{ix})^{*}(e^{ix})=(\cos(x)-i \sin(x))(\cos(x)+i \sin(x))=\cos^2(x)-i^2 \sin^2(x)=\cos^2(x)+\sin^2(x)=1$

Как-то Вы сложно, можно и без тригонометрии.
$(e^{ix})^{*}=e^{-ix}$, поэтому $(e^{ix})^{*}(e^{ix})=(e^{-ix})(e^{ix})=e^0=1$

[pppppppo_98]

B3LYP в сообщении #1623100 писал(а):

Почему вы пишете $a(q)$, а не $\Psi(x)$?

потому что человек перешел от координатного представления (базиса $\dela(x-x_0)$) к импульсному(базису $\frac{1}{\sqrt{2 \pi}}e^{i k_0 x}$) и амплитуда теперь зависит от импульса (не нравится обозначение $a(q)$ замените на $\Psi(q)$. Это делается с помощью преобразования Фурье (унитарного кстати). Если бы вы прочитали какой учебник по урав
нениям математической физики, то знали , что это частый прием для решения уравнений с постоянными коэффициентами на евклидовом пространстве.

B3LYP url=http://dxdy.ru/post1623100.html#p1623100]сообщении #1623100[/url] писал(а):

Мне трудно изучать такие предметы по учебникам. Раньше не мог выучить Delphi и ООП по книгам, а потом пошёл на платные курсы и преподаватель мне на пальцах всё объяснил.

И такой бывает психотип людей... Только тут надо напрягаться... Область настолько узкая и настолько требует значительных ресурсов на изучение предварительного материала, что вы вряд ли не найдете никаких платных интерактивных курсов да еще на русском языке, где бы вас за месяц обучили всему предварительному материалу и самой КМ. Есть конечно курсы американских универов (но вот уж не знаю насколько вам удастся с преподавателем общаться)

ЗЫ

Не возможно научить женщину рожать ребенка за 1 месяц.

пианист в сообщении #1623105 писал(а):

$(e^{ix})^{*}=e^{-ix}$, поэтому $(e^{ix})^{*}(e^{ix})=(e^{-ix})(e^{ix})=e^0=1$

PPS

Я вот примерно прикинул. Перед курсом КМ, у нас было 540 часов матана (последний семестр основы функциональногот анализа), 270 часов дифференциальных уравнений, 140 часов уравнений математической физики, 140 часов теоретической механики, 140 часов линейно алгебры

И это тоже сложно. Нужно с азов $(a +b\,i)^*=a-b\,i $. И формула Эйлера $e^{i\phi}=\cos{\phi}+i\sin{\phi}$

[B3LYP]

Продолжаю смотреть Дэйва, про барьер:

https://youtu.be/kUR98x1tH0c

Повторю начальные формулы:


$\psi (x)=A e^{i k_0 x}+B e^{-i k_0 x}$

При x<0

$\psi (x)=C e^{i k_0 x}$

При x>a

$\psi (x)=F e^{k_b x}+F e^{-k_b x}$

При 0<x<a

$k_0=\frac{\sqrt{2m E}}{\hbar}$

$k_b=\frac{\sqrt{2m (U_0 - E)}}{\hbar}$

Рассмотрение граничных условий (равенство волновых функций и их первых производных) даёт систему уравнений:

$A+B=F+G$
$ik_0 A -ik_0 B=k_b F - k_b G$
$F e^{k_{b}a}+G e^{-k_{b}a}=C e^{i k_0 a}$
$k_b F e^{k_{b}a}-k_b_ G e^{-k_{b}a}=i k_0 C e^{i k_0 a}$

Решение этой системы приводит к

$\frac{C}{A}=(1+\frac{\sinh^2(k_b a)}{4 \eta(1-\eta)})^{-0.5}$
$\eta=\frac{E}{U_0}$

Далее по этой формуле Дэйв проводит расчёты: если высота барьера 1 микроэлектронвольт, и толщина барьера 0.1 нанометр, то тоннельный эффект хорошо проявляется (например при энергии электрона в 20% от энергии барьера, почти 20% электронов проходят сквозь барьер).
Если же энергия частицы выше барьера, то получится формула:

$\frac{C}{A}=(1+\frac{\sin^2(k_b a)}{4 \eta(1-\eta)})^{-0.5}$

И тут получается второй интересный эффект - осцилляции: т.к. в формуле синусоида, увеличение энергии электрона приводит к чередованию роста уровня прохождения через барьер и спада. Эта синусоида хорошо заметна, если энергия барьера 1 mEV и толщина барьера 1 нанометр.
Просьба прокомментировать.

[pppppppo_98]

B3LYP в сообщении #1623776 писал(а):

если высота барьера 1 микроэлектронвольт, и толщина барьера 0.1 нанометр, то тоннельный эффект хорошо проявляется (например при энергии электрона в 20% от энергии барьера, почти 20% электронов проходят сквозь барьер).

лажа какая-то.... средняя кинетическая энергия электрона на одну степень свободы $\frac{k T}{2}=12.5$ мэВ... Такшо барьер в 1 микроэлектронвольт вообще никакой электрон не заметит в реальном материале. Характерные энергии ковалентной связи порядка десятых эв, водородной тоже порядка десятка мэВ...

[revos]

Микрочастица наиболее сильно проявляет волновые свойства в условиях, когда её длина волны де Бройля $\lambda$ по порядку величины равна длине, на которой существенно меняется внешнее поле, $a$ :
$\lambda =\frac{\hbar}{p} =\frac{\hbar}{\sqrt{2mE}}\sim a$, откуда $ E\sim\frac{1}{2m}(\frac{\hbar}{a})^2$. Подставляя в оценочную формулу, массу электрона $m$, значение постоянной Планка $\hbar$ и $a$= 0,1 нанометр, получите $ E\sim$ 3,8 МэВ (мегаэлектронвольт). Но никак не "микроэлектронвольт".

Цитата:

Просьба прокомментировать.

Кроме туннельного эффекта есть явление надбарьерного отражения.

[pppppppo_98]

revos в сообщении #1623832 писал(а):

Микрочастица наиболее сильно проявляет волновые свойства в условиях, когда её длина волны де Бройля $\lambda$ по порядку величины равна длине, на которой существенно меняется внешнее поле, $a$ :
$\lambda =\frac{\hbar}{p} =\frac{\hbar}{\sqrt{2mE}}\sim a$, откуда $ E\sim\frac{1}{2m}(\frac{\hbar}{a})^2$. Подставляя в оценочную формулу, массу электрона $m$, значение постоянной Планка $\hbar$ и $a$= 0,1 нанометр, получите $ E\sim$ 3,8 МэВ (мегаэлектронвольт). Но никак не "микроэлектронвольт".

и тоже уважаемый не так... Обычные барьеры имеющие практческое значение в электронике и химии - порядка 1 эВ... 3.5 Мэв - это туннельный переход соответствующий ядерному нуклеосинтезу, а это на 5 порядков меньше характерный размер

http://nuclphys.sinp.msu.ru/enc/e122.htm

по вашей формуле при a равному 1 ангстрему у меня получается характерный масштаб энергии порядка 3 эВ

[Cos(x-pi/2)]

pppppppo_98, да. Вы опередили меня, пока я медленно печатал свой вот такой ответ:

revos
Не надо в ПРР писать бредовые числа. Длина $a=0.1 \text{ нм}$ это один ангстрем - величина порядка линейного размера электронной оболочки атома; характерный атомный масштаб энергии электрона - порядка нескольких электронвольт. Подставив $a=0.1 \text{ нм}$ в формулу $\frac{\hbar^2}{2ma^2},$ получим $3.82$ эВ но никак не мегаэлектронвольты!

Заодно приведу точную формулу длины волны де Бройля. $\frac{p}{\hbar}=k$ есть величина волнового вектора, а соответствующая волновому вектору длина волны (т.е. расстояние, на котором фаза $kx$ волны изменяется на $2\pi)$ есть $\lambda=\frac{2\pi}{k}.$ Поэтому в формуле де Бройля для длины волны надо писать множитель $2\pi,$ т.е. $\lambda=\frac{2\pi\hbar}{p}.$ А если пишете без множителя $2\pi,$ то тогда постоянная Планка должна быть "без планки": $h=2\pi\hbar.$

Автор того видео, которое смотрит ТС, тоже перепутал $\hbar$ с $h$ и дал неверное числовое значение для $\hbar.$ А с числовым значением массы электрона автор видео вообще дико наврал - он поделил мегаэлектронвольты на скорость света, забыв возвести её во вторую степень. Ну и, конечно, утверждение, будто для электронов в приборах характерный масштаб барьера это микроэлектронвольт и будто лишь 20% электронов туннелируют через такой барьер, - чушь.

[pppppppo_98]

Cos(x-pi/2) в сообщении #1623838 писал(а):

Автор того видео, которое смотрит ТС, тоже перепутал $\hbar$ с $h$ и дал неверное числовое значение для $\hbar.$ А с числовым значением массы электрона автор видео вообще дико наврал
- он поделил мегаэлектронвольты на скорость света, забыв возвести её во вторую степень. Ну и, конечно, утверждение, будто для электронов в приборах характерный масштаб барьера это микроэлектронвольт и будто лишь 20% электронов туннелируют через такой барьер, - чушь.

есть такой принцип образования (увы)...Можешь - делай, не можешь - иди учить, не можешь учить - иди учить как учить... автор видео похоже вообще не вкуривает масштабы явлений - за отсутствием знаний матчасти....1 $\mu$эВ - соотвтествует температруе в 10 мК, вполне достижимая в современной криогенике, но не имеет отношения к микроэлектронике

[Cos(x-pi/2)]

Заодно добавлю ещё комментарий к самой учебной задаче о туннелировании и отражении частицы от барьера. В этом сюжете есть ещё один примечательный эффект - задержка отражаемого волнового пакета.

(Выше я приводил графики с приближённым расчётом волновой функции, как интегральной суперпозиции стационарных решений с близкими значениями волнового вектора $q.$ Приближение состояло в том, что с коэффициентной функцией $a(q)$ интегрировались по $q$ только экспоненты с мнимым показателем, имеющиеся в стационарном решении и содержащие $q,$ а все остальные сомножители брались при $q=q_0.$ Такие интегралы были "гауссовские", что позволило найти приближённое выражение для $|\Psi(x,t)|^2$ в аналитическом виде - это основное преимущество такого приближённого расчёта. Но при этом "эффект задержки" отражённого волнового пакета оказался утерян, и появился артефакт - протуннелировавший пакет сдвинут от барьера на длину барьера, т.е. получившаяся приближённая картина в деталях не точна.

В "точном" расчёте интегрируются по $q$ все величины, зависящие от $q.$ Такое интегрирование удаётся выполнить лишь численно, и в этом смысле оно приближённое. При этом артефакта нет, а эффект задержки виден. Вот для сравнения старый график с удаляющимися от барьера отражённым и протуннелировавшим волновыми пакетами в приближённом расчёте, и аналогичный результат точного расчёта; сравнивать следует координаты $x$ максимумов волновых пакетов.)

Эффект задержки волнового пакета при отражении от барьера подробно рассмотрен в некоторых учебниках по квантовой механике, а также - в решении задачи 6.7 в книге:

"Задачи по квантовой механике" В.М. Галицкий, Б.М. Карнаков, В.И. Коган, М.: Наука, 1992.

(Это задачник с решениями; рекомендуется всем взявшимся всерьёз изучать КМ. В раннем, первом его издании решений не было. Наверное существуют и более современные издания этого задачника.)

[B3LYP]

Грустно что Дэйв оказался таким бестолковым, но мне нравится его смотреть, по-моему он хорошо объясняет, плюс я так учу английский. Вот ещё раз выведенные им формулы для коэффициента отражения:

$\frac{C}{A}=(1+\frac{\sinh^2(k_b a)}{4 \eta(1-\eta)})^{-0.5}$

При $\eta<1$

$\frac{C}{A}=(1+\frac{\sin^2(k_b a)}{4 \eta(1-\eta)})^{-0.5}$

При $\eta>1$

$\eta=\frac{E}{U_0}$

$k_b=\frac{\sqrt{2m (U_0 - E)}}{\hbar}=\frac{\sqrt{2m U_0 (1- \eta)}}{\hbar}$

Это правильно?
И ещё математический вопрос: как получается, что гиперболический синус переходит в обычный синус? Там же должен быть разрыв второй или какой-то там производной, это нормально?

[Cos(x-pi/2)]

B3LYP в сообщении #1623875 писал(а):

Грустно что Дэйв оказался таким бестолковым, но мне нравится его смотреть, по-моему он хорошо объясняет, плюс я так учу английский. Вот ещё раз выведенные им формулы для коэффициента отражения: <...> Это правильно?

"Нравится смотреть" это не то же самое, что "понимать объяснения". Если бы его объяснения были хороши для Вас, то Вы не задавали бы свой постоянный вопрос "Это правильно?"

Приведённые Вами формулы для $\frac{C}{A}$ имеют смысл модуля комплексной амплитуды вероятности прохождения (а вовсе не отражения!) частицы за барьер; ну или за яму, если $U_0<0.$ В квантовой механике модули комплексных амплитуд вероятности люди вычисляют для того, чтобы возвести их в квадрат: квадрат модуля амплитуды вероятности имеет смысл вероятности. В данной задаче вероятность прохождения есть $|\frac{C}{A}|^2,$ т.е. она даётся не самими указанными Вами выражениями, а возведёнными в квадрат выражениями.

B3LYP в сообщении #1623875 писал(а):

И ещё математический вопрос: как получается, что гиперболический синус переходит в обычный синус? Там же должен быть разрыв второй или какой-то там производной, это нормально?

Это же элементарная алгебра: напишите явную формулу для $\sinh(z)$ через экспоненты, подставьте $z=ix,$ и посмотрите, как получившаяся формула связана с выражением для $\sin(x)$ через экспоненты. Такие экспоненты и все их производные непрерывны.

B3LYP, Вам уже самое главное объяснили: нет путей в науку без книг и без самостоятельных упражнений. Садитесь за учебники и задачники, и с ручкой на бумаге тренируйтесь выводить и тем самым проверять интересующие Вас формулы, - только так у Вас появится шанс разобраться. Ну а если это для Вас слишком трудно, и напрягаться не хочется, то честно скажите себе: "физика и математика - это не моё", и забейте.

(На этом заканчиваю сюда вмешиваться. Ваши пересказы (непонятно с какой целью) простых учебных формул из видеоролика с неизменным вопросом "Это правильно?" вместо попыток изучать книги и самостоятельно проделывать выкладки, чтобы отвечать себе на такой вопрос, похожи на троллинг.)