Реализация “Аб иницио” подхода в молекулярной механике

[B3LYP]

В тему приглашаются физики, физхимики, химики-квантовики и химики-органики.
У меня есть идея сделать реализацию молекулярной механики. Говорят что современная ММ иногда неплохо работает, например позволяет находить конформации органических молекул. И создалось ощущение, что я могу придумать некий новый подход.
Общая мысль у меня такая. Мы проводим с квантовохимическим методом, например DFT, расчёт молекулы, и далее используем результаты расчёта как выборку для обучения функционала молекулярной механики, или как это назвать, ну в общем мы подгоняем параметры нашего ММ функционала так, чтобы получилось наибольшее согласие с результатами DFT расчёта. И далее полученный кастомный ММ функционал мы используем, чтобы посчитать более сложную задачу, для которой исходный DFT метод слишком дорогостоящий. Как пример: мы посчитали на DFT гармонический колебательный спектр (вторые производные энергии по координатам атомов), далее загоняем силовое поле и другие параметры для подгонки ММ функционала, и далее полученный ММ функционал используем для расчёта ангармонического силового поля (третьи и дальнейшие производные по энергии), и это позволит предсказывать обертоны в колебательном спектре, или например более точную колебательную энтропию.
Так вот. Для такого подхода нужно реализовывать ММ модель такую, чтобы ММ расчёт в ней был скорее не “хороший”, а “неэмпиричный”. Т.е. эта ММ модель должна основываться на каких-то универсальных, фундаментальных принципах, тогда в общем случае подгонка параметров ММ функционала будет работать неплохо.
Что я имею в виду под фундаментальными принципами? Ну например стерическое отталкивание. Очевидно, можно считать универсальным принципом, что несвязанные атомы обычно отталкиваются. Какими моделями лучше это описать?
Может быть я немного путаю; верно ли что потенциал Морзе относительно хорошо описывает поверхность потенциально энергии (ППЭ) двухатомных молекул? Насколько этот потенциал универсален и “неэмпиричен”?
Методы квантовой химии делятся на неэмпирические (ab initio) и эмпирические подходы. Ab initio подход означает, что мы проводим расчёт свойств молекулы, решая уравнение Шредингера; при этом мы используем только знания квантовой механики и универсальных физических постоянных. Но ab initio подход часто слишком дорогостоящий, т.е. ресурсов компьютера не хватает для его использования; и тогда мы вводим разные приближения плюс подгоночные параметры, которые подгоняем под данные эксперимента для изучаемых молекул. Это называется эмпирическим подходом, и он менее универсален — для молекул, по которым мы делали подгонку, он может и будет работать, а для непохожих систем уже нет.
Если тема найдёт интерес, я дальше напишу конкретную идею реализации молекулярной механики; кратко говоря, я предлагаю полностью отказаться от валентных углов как параметризуемых переменных ММ, а вместо этого добавлять везде, где есть неподелённые электронные пары, фиктивные атомы, которые отталкиваются так же как обычные атомы, и за счёт этого создают правильные валентные углы.

[madschumacher]

B3LYP в сообщении #1626146 писал(а):

Общая мысль у меня такая. Мы проводим с квантовохимическим методом, например DFT, расчёт молекулы, и далее используем результаты расчёта как выборку для обучения функционала молекулярной механики, или как это назвать, ну в общем мы подгоняем параметры нашего ММ функционала так, чтобы получилось наибольшее согласие с результатами DFT расчёта. И далее полученный кастомный ММ функционал мы используем, чтобы посчитать более сложную задачу, для которой исходный DFT метод слишком дорогостоящий. Как пример: мы посчитали на DFT гармонический колебательный спектр (вторые производные энергии по координатам атомов), далее загоняем силовое поле и другие параметры для подгонки ММ функционала, и далее полученный ММ функционал используем для расчёта ангармонического силового поля (третьи и дальнейшие производные по энергии), и это позволит предсказывать обертоны в колебательном спектре, или например более точную колебательную энтропию.

Так такое много уже раз делали. Там и on-the-fly обучение нейросеток бывает, и экстраполяция полей, и много извращений на разный вкус. Прям из относительно свежего, известного, и буквально того, что Вы хотите, это делал Штефан Гримме. Называется эта штука QMDFF, и можно почитать об этом в статье "A General Quantum Mechanically Derived Force Field (QMDFF) for Molecules and Condensed Phase Simulations".

B3LYP в сообщении #1626146 писал(а):

Если тема найдёт интерес, я дальше напишу конкретную идею реализации молекулярной механики; кратко говоря, я предлагаю полностью отказаться от валентных углов как параметризуемых переменных ММ, а вместо этого добавлять везде, где есть неподелённые электронные пары, фиктивные атомы, которые отталкиваются так же как обычные атомы, и за счёт этого создают правильные валентные углы.

Ну так это реинкарнация модели Гиллеспи, известной также как теория отталкивания электронных пар валентной оболочки (ОЭПВО), а она хоть полезна и крута, но много где лажает. И в силовых полях такое тоже используется повсеместно, в частности из простого, это модельные ММ поля для воды, типа TIP4P, TIP5P, TIP6P и т.д.

[Утундрий]

B3LYP в сообщении #1626146 писал(а):

создалось ощущение, что я могу придумать некий новый подход.

В пятке?

[B3LYP]

madschumacher в сообщении #1626313 писал(а):

Прям из относительно свежего, известного, и буквально того, что Вы хотите, это делал Штефан Гримме. Называется эта штука QMDFF, и можно почитать об этом в статье "A General Quantum Mechanically Derived Force Field (QMDFF) for Molecules and Condensed Phase Simulations"
.

Да, это очень похоже на то что предлагаю здесь я, только я полагаю, что если Гримме использовал бы модель ММ “пофизичнее”, которую я предлагаю, результат был бы ещё лучше.
Вот как мне это видится. Возьмём молекулу аммиака NH3: это пирамида с углом H-N-H около 106 градусов. Если модель ММ как-то задаёт этот угол в роли параметра, по-моему это сильно некрасиво. Лучше рассматривать неподелённую электронную пару у азота как “атом” со своими параметрами; тогда естественным образом получается, что молекула NXH3 вследствие отталкивания между атомами водорода и этим фиктивным атомом образует примерно тетраэдр:



При подгонке параметров ММ функционала под хороший расчёт, мы можем варьировать какие-то параметры этого фиктивного атома, и параметры атомов водорода и азота; по идее, надо варьировать размер и анизотропию электронных облаков. Чтобы мой вопрос стал более понятен, нарисую в этой модели молекулу этанола:



Какие параметры мы должны фиттить, чтобы подобрать ММ функционал? Очевидно что прежде всего это параметры для связей C-O, C-H, O-H, O-X, скажем параметры потенциала Морзе. Что ещё? Я утверждаю что подгонять параметры углов – плохая затея. Можно подгонять параметры взаимодействий для несвязанных расстояний – C..H, H..H, H..O и пр.. Потенциал Леннарда-Джонса, полагаю, тут не очень сгодится, надо что-то погибче. Вообще надо понимать, что число варьируемых параметров надо сводить к минимуму – иначе согласие для данного конкретного фита будет хорошее, а вот для новых задач полученный ММ функционал не сгодится.
Я вот думаю: а что если не подгонять даже несвязанные расстояния, а вместо этого считать каждый атом неким электронным облаком (вокруг ядра, кроме X атомов), и считать электростатическое взаимодействие исходя из этого? Я имею в виду, что мы будем варьировать скажем размер электронного облака и несколько параметров его анизотропии (асимметрии).
Хотя я не исключаю и вариант что ерунду пишу, поскольку, как я понимаю, дисперсионные взаимодействия это не только отталкивание но ещё и притяжение, и они в эту схему не впишутся. Значит надо лучше представлять, что такое дисперсионные взаимодействия.

[madschumacher]

B3LYP в сообщении #1631528 писал(а):

Возьмём молекулу аммиака NH3: это пирамида с углом H-N-H около 106 градусов. Если модель ММ как-то задаёт этот угол в роли параметра, по-моему это сильно некрасиво. Лучше рассматривать неподелённую электронную пару у азота как “атом” со своими параметрами; тогда естественным образом получается, что молекула NXH3 вследствие отталкивания между атомами водорода и этим фиктивным атомом образует примерно тетраэдр:

Ну я же выше уже отвечал Вам, что такое делали уже, оно уже существует, и если хотите, можете это использовать уже готовое:

madschumacher в сообщении #1626313 писал(а):

Ну так это реинкарнация модели Гиллеспи, известной также как теория отталкивания электронных пар валентной оболочки (ОЭПВО), а она хоть полезна и крута, но много где лажает. И в силовых полях такое тоже используется повсеместно, в частности из простого, это модельные ММ поля для воды, типа TIP4P, TIP5P, TIP6P
и т.д.

Из тех проблем, что я не указал, это то что каждый такой фиктивный атом удорожает молдинамику, потому что его нужно учитывать как полноценный атом. Для каких-нибудь 100-атомных систем разницы нет, но реальные поля нужны для тысяч-миллионов атомов, и там уже такой кратный прирост стоимости уже неприятен.

B3LYP в сообщении #1631528 писал(а):

Я утверждаю что подгонять параметры углов – плохая затея.

1) По факту, пофиг чем аппроксимировать (тут, в частности, в примеры идут нейросети и полиномы. 2) То, что Вы предлагаете, уже существует, и по результату, получается, что углы лучше, поэтому люди их используют.

[B3LYP]

Кажется я созрел до реальной работы над этой задачей, готов скоро приступить.
Сейчас я сделал программу, которая запускает программу xtb, та делает single point расчёт энергии и её градиентов, далее моя программа читает файл xtb и итерация повторяется. Что-то близкое сделал Артём Оганов в своём Успехе, как я понимаю.
Текущий алгоритм оптимизации крайне примитивный: к координатам атомов добавляются градиенты, умноженные на какой-то коэффициент. Если на следующем шаге энергия получилась ниже – система возвращается к предыдущим координатам, и этот коэффициент уменьшается.
Интересно сейчас получилось - такая молекула, как бензол, оптимизируется нормально, в то время как например пропан очень долго (если у пропана повернуть метильные группы вокруг связи C-C, они никак не соптимизизируются в правильное положение). Предлагаю догадаться, почему так получается. Вот структуры этих молекул:





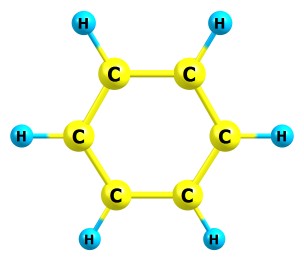
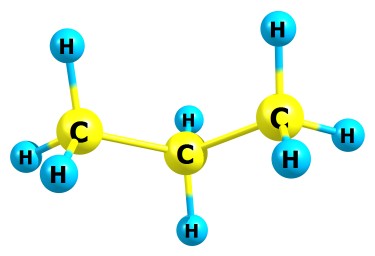
Итак, каким у меня будет алгоритм: я сделаю кастомный ММ функционал, и его параметры будут динамически подгоняться под квантовохимический расчёт. Я не хочу изучать литературу по молекулярной механике, поскольку, как мне кажется, у меня лучше получится сразу придумать что-то своё, учитывая что я уже 20 лет занимаюсь структурной и квантовой химией. В моём алгоритме будут следующие параметры: три коэффициента для потенциала Морзе для каждой связи, и по два параметра для каждого атома, определяющих значения коэффициентов для потенциала Леннарда-Джонса с этим атомом, точнее определяющих как бы способность атома притягивать другие атомы с энергией, обратно пропонциональной шестой степени от расстояния, и отталкивать их с энергией, обратно пропорциональной двенадцатой степени. Понятно ли кому-то, о чём я говорю?
Возьмём для примера молекулу толуола:



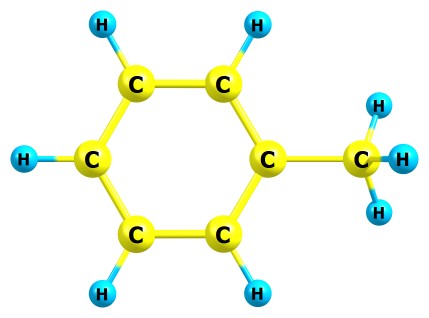
Здесь 15 атомов и 15 связей. Значит суммарное число параметров будет $15 \cdot 2+15 \cdot 3=75$. Эти параметры будут фиттиться на каждом шаге оптимизации.
Когда будет посчитана первая точка, расчёт даст только градиенты, т.е. этот расчёт покроет $15 \cdot 3=45 $степеней свободы (из них ещё 6 избыточных). Это значит, что фиттить ММ параметры неосторожно будет нельзя, иначе система улетит. Если же расчёт дойдёт до точки минимума и посчитаются частоты (вторые производные), он даст $45 \cdot 46/2=1035$ чисел, этого разумеется хватит для фита, и надо будет добавить ещё какие-то параметры, чтобы не недофитилось (недоиспользование данных расчёта частоты). Продолжение следует.