Спасибо всем, кто мне помогал.
Просто двигаем 1 вершину и получаем что она в самой далекой вершине многоугольника от противоположной стороны треугольника. По-очереди задвигаем все вершины треугольника в углы многоугольника.
вписанный треугольник наибольшей площади"... такой треугольник существует, назовем его

. Построим треугольник, для которого треугольник

является серединным. Площадь построенного треугольника в четыре раза больше площади треугольника

. Построенный треугольник содержит исходный многоугольник. Задача решена.
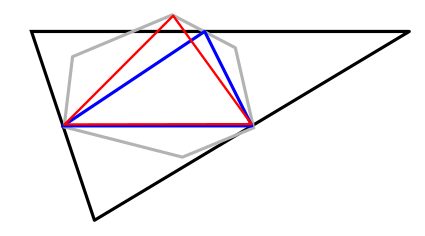
Если бы многоугольник вылез за пределы черного треугольника, синий треугольник не имел бы максимальную площадь: красный имеет с синим одно основание, но большую высоту.
,
TOTAL,
svv, я честно пыталась, но в Ваше решение вьехать не смогла, наверно слишком сложно для меня.
Gagarin1968, но Ваше решение, на мой взгляд, понятнее — там ничего не надо дополнительно пояснять.
Точно, это решение до меня наконец дошло.
Я бы начал так.
Возьмём в многоугольнике две точки

и

, наиболее удалённые друг от друга. Строить эти точки не надо, достаточно утверждать, что они существуют. Через эти точки проведём прямые

и

соответственно перпендикулярно отрезку

.
Получим область, заключённую между этими параллельными прямыми. Никакая точка многоугольника не может лежать вне этой области. Действительно, если, скажем, некоторая точка

находится снаружи этой области, то полагая без потери общности

, видим, что в треугольнике

угол

— тупой, и следовательно,

, что противоречит предположению о максимальности отрезка

.
А дальше я предлагаю ТС найти точку

многоугольника, максимально удалённую от прямой

, и продолжить решение.
Продолжить, я думаю, можно так:
Пусть расстояние между точкой

и прямой

будет

. Тогда проведём 2 прямые

и

параллельно

на расстоянии

от неё по обе стороны от

.
По тем же самым соображениям, которые привёл
Gagarin1968, никакая точка многоугольника не может быть снаружи области, ограниченной прямыми

и

, т.к. иначе расстояние от

до этой точки будет больше

.
Таким образом я получила, что данный многоугольник лежит целиком внутри прямоугольника, образованного прямыми

,

,

,

.
Площадь треугольника

равна

.
Площадь прямоугольника равна

.
А соотношение площадей равно

, что и требовалось доказать.
Так правильно?
P.S. Это соответствует рисунку, который привел
wrest:



