Stephen Walker, sergey zhukov, лучше постройте координаты Эддингтона-Финкельштейна
Да, координаты Шварцшильда не слишком хороши своей координатной сингулярностью на горизонте, а кроме того - линии

пространственноподобны только над горизонтом, а под ним - времениподобны, что приводит к путанице и "двойникам". Лучше взять координаты, в которых линии

пространственноподобны везде.
Нетрудно построить пример координат, которые не покрывают всего пространства-времени и имеют сингулярности. Например, если на графике равномерного движения частицы по каким-либо причинам использовать координатные метки времени, которые достигают бесконечности при конечном собственном времени частицы, то это приводит к неполному покрытию координатами пространства-времени, и часть мировой линии частицы просто "исчезает" в таких координатах. Если же после "переваливания через бесконечность" метки времени идут в обратном порядке, то в таких координатах мы получаем "двойников":
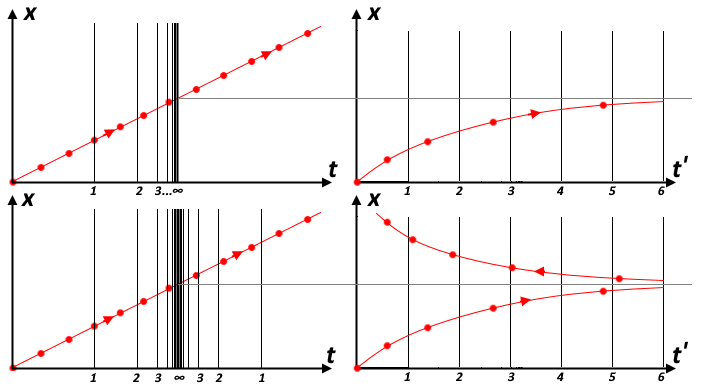
Нечто подобное происходит и с координатами Шварцшильда: линия горизонта "сдвигает в бесконечность" события, которые лучше бы отобразить без сдвига. Координаты Финкельштейна - это просто координаты Шварцшильда, сдвинутые по вертикали вниз таким образом, чтобы луч света, радиально падающий в ЧД (желтый), стал прямым (для этого требуется бесконечный сдвиг вдоль прямой горизонта, сингулярные координаты требуют сингулярных преобразований, чтобы получилось что-то гладкое):
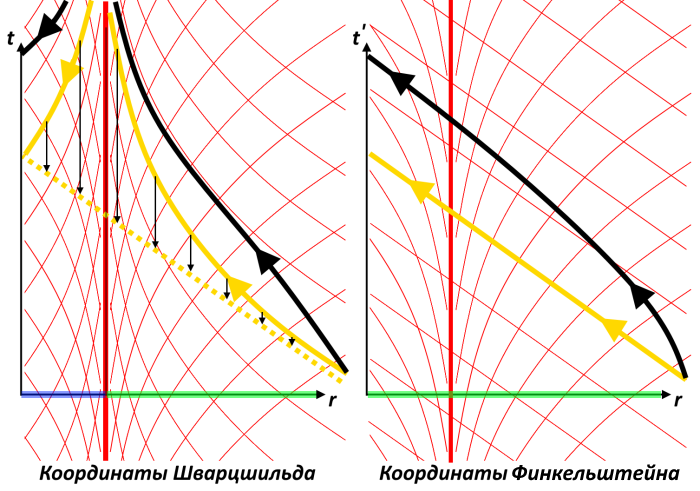
(На первом рисунке лучи света должны упираться в линию сингулярности под прямым углом, я не стал тут рисовать точно. На втором рисунке сдвиг действует на все лучи света, но те, которые "не выпрямляются", делаются еще "более сингулярными", так что я не стал их перерисовывать, т.к. их вид качественно не меняется). Сдвиг приводит к тому, что лучи света, пересекающие горизонт, становятся прямыми, мировые линии падающих в ЧД частиц (черная) больше не "переваливают через бесконечность", а линии

- всюду становятся пространственноподобными (зеленые).
Вообще, линии

определяются произвольным выбором координат. Когда мы задаем вопрос "Пересечет ли когда-нибудь падающее тело горизонт событий ЧД для внешнего наблюдателя?", то не хотели бы, я думаю, услышать "Это зависит от того, как мы определим координатные гиперповерхности

", т.к. мы уверены, что координаты тут точно ни при чем. Должны иметь значение только объективные вещи - причинно-следственная структура пространства-времени, области абсолютного прошлого (световой конус прошлого) и абсолютного будущего (световой конус будущего) для наблюдателя. Тогда можно сказать, что для внешнего наблюдателя существует вполне определенный момент собственного времени, когда событие пересечения падающим телом горизонта ЧД перестает быть его абсолютным будущим, но это событие никогда не становится его абсолютным прошлым. Оно навсегда остается в пространственно отделенной области.
В пространстве-времени Галилея удаленное событие может быть либо в абсолютном будущем, либо в абсолютном прошлом наблюдателя. И есть момент перехода из одной области в другую (сейчас). В СТО и ОТО этот "момент перехода" вырос до области, в которой помещается больше событий, чем в прошлом и будущем, вместе взятых. События из этой области можно произвольно назначать одновременными с событием в вершине конуса. Т.е. в СТО и ОТО событие может перестать быть будущим, но оно еще долго (или вообще никогда) не станет прошлым. Можно ли сказать, что в этом случае события для наблюдателя не было? Пожалуй, можно лишь сказать, что для данного наблюдателя оно никогда не станет его прошлым, но нельзя сказать, что оно не было одновременным с каким-либо событием на мировой линии наблюдателя.



