
обозначает множество, состоящее ровно из одного элемента, а именно, из
значения переменной  .
.(Выделение жирным шрифтом мое.)
Спасибо, такой взгляд мне многое об'ясняет. Но хотелось бы заметить, что в фигурных скобках могут стоять не только переменные, но и постоянные.
Обозначения об'ектов бывают постоянные и переменные, и в записи множества в фигурных скобках могут стоять как переменные, так и постоянные обозначения об'ектов.
Постоянные обозначения об'ектов являются их индивидуальными обозначениями. Цифра

обозначает наименьшее по величине натуральное число, и только его (во всяком случае в пределах настоящего сообщения), цифра

обозначает следующее по величине натуральное число, и только его, и т. д..
В отношении идентификации это очень хорошие обозначения: когда мы видим запись

, нам ясно, что об'ектом, из которого состоит множество

, является число

. И также
понятно, что

.
Но в отношении переменных дело обстоит несколько сложнее.
Переменное обозначение об'ектов является их общим (а не индивидуальным) обозначением.
(Пусть

. Здесь

это обозначение каждого из натуральных чисел, это как бы фамилия всех братьев (или сестер), имена которых

. То есть каждое натуральное число имеет два обозначения -- постоянное и переменное.)
Поэтому, когда мы видим запись

, мы не можем сказать, из какого об'екта состоит множество

, ясно только, что это всего один об'ект.
А когда мы видим запись

, мы видим, что мощность множества

может быть от

до

, из каких же именно об'ектов оно может состоять прямо зависит от того, какие значения могут принимать переменные
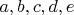
.
Что вы тогда тут голову всем морочите? 9 страниц бессмыслицы.
Это для Вас это девять страниц бессмыслицы, потому что Вы все это знаете, но не для меня.