Vladimir PliassovДавайте так. Любое утверждение из теории множеств является утверждением об объектах, не об именах объектов. Внутри теории множеств имена объектов не имеют никакого значения. Вам, грубо говоря, пытаются сказать, что, хотя "1+1" и "2" это разные наборы символов, 1+1 и 2 это
одно и то же. Утверждение

есть утверждение об объектах

,

,

: оно значит, что

,

, а всё, что не

и не

,

. Но здесь мы не можем сказать, разные

и

объекты или один и тот же. Из того, что "

" и "

" — разные буквы, не следует, что

и

— разные объекты.
Ваши подсчёты типа "Вот здесь одно имя объекта. О, а здесь их пять!" очень странны. Во первых, чему угодно можно приписать сколько угодно имён. Во вторых, и это самое важное, от таких подсчётов в теории множеств не зависит ровным счётом ничего. Вам сказали разделять объекты и их имена, чтобы вы отдалились от имён и сконцентрировались на объектах, а вы сделали наоборот.
Отвечая на ваш старый вопрос,
Пусть нам дана совокупность

множеств

:

, где

, и при этом

.
Значит ли это, что речь здесь идет о двух одинаковых объектах
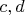
?
Если

, то для теории множеств нет никакой разницы между

и

. Это для вас "

" и "

" — разные буквы. В рамках теории множеств

и

— просто одно и то же, точно так же, как Vladimir Pliassov и Vladimir Pliassov — одно и то же.
По поводу мультимножеств: нет никаких мультимножеств. В книгах, которые Вам предлагали, ни разу не звучит слово "мультимножество", а когда говорят а мультимножествах
всегда указывают, что речь идёт именно о мультимножествах. Для любого множества

и объекта

выполняется либо

, либо

. В теории множеств это всё, что имеет значение. Если мы пишем

, это по определению значит, что

,

, и для любого

такого, что

и

выполняется

. Отсюда сразу видно, что

содержит ровно те же элементы, что

(то есть двойку и больше ничего)