math.fi1) Правильно набирайте все формулы, даже состоящие из одной буквы:
В параллелограмме
ABCD 
отмечены середины
E,F 
...
и так далее.
2) Векторы применены совершенно не по делу. Вектор на вектор делить нельзя (такого действия в математике нет), да и не нужно, так как по смыслу у Вас просто отношение длин отрезков.
3) Точка

ни в каком отношении не делит отрезок
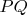
, так как она ему не принадлежит (во всяком случае, на чертеже).
4a) В условии сказано, что прямая

пересекает прямую

в точке

, но на чертеже это не так. Либо условие неверное, либо чертёж.
4b) В условии сказано, что прямая

пересекает прямую

в точке

, но на чертеже это не так. Либо условие неверное, либо чертёж.
4c) В условии сказано, что прямая

пересекает прямую

в точке

, но на чертеже это не так. Либо условие неверное, либо чертёж.



