Задача на деление отрезка в данном отношении.

[math.fi]

dxdy, помоги пожалуйста разобраться с задачей.

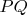
В параллелограмме $ABCD$ отмечены середины $E,F$ сторон $AB$ и $CD$ соответственно. Прямая $l$, не проходящая через точку $E$, пересекает прямые $AB, EF, CE \text{ и } DE$ в точках $P, Q, R \text{ и } S$ соответственно. Точка $R$ делит отрезок $PQ$ в отношении $\lambda$. В каком отношении делит этот отрезок точка $S$?


Нужно как-то выразить все через $\overrightarrow{PQ} и $\overrightarrow{QR}$, но я застрял на этой задаче. Вот, можно еще так, но это так или иначе приводит к тому, что нужно узнать как выразить [math]$SQ$[/math]:
$\frac{\vec{PS}}{\vec{SQ}} = \frac{\vec {PQ}}{\vec{SQ}} -1 $

Вообще не понятно к чему привязаться. Теорема Менелая не особо помогла, но есть вероятность, что я ее просто не умею.

По просьбе форумчан про теорему Менелая.
Собственно теорема менелая это было последнее, что я попробовал.
Идея у меня была простая:
1. известно только отношение $\overrightarrow{PQ} \text{ и } \overrightarrow{QR}$, значит нужно через них выразить $\overrightarrow{PS} \text{ и } \overrightarrow{SQ} $;
2. нужно подобрать какой-то базис: мне показалось, что неплохо выглядят в этой роли $\overrightarrow{EP} \text{ и } \overrightarrow{EQ}$ (не знаю почему - душа так легла);
3. с векторами мы можем немного: сложить и умножить на число, например длину другого вектора;
немного покрутив выражения векторов, типа:
$\overrightarrow{ER} = \overrightarrow{EP} + \overrightarrow{PR} | \cdot QR$
$\overrightarrow{ER} = \overrightarrow{EQ} + \overrightarrow{QR} | \cdot PR$
и учитывая, что:
$\overrightarrow{PR}QR + \overrightarrow{QR}PR = 0$
мы получим:
$\overrightarrow{ER}PQ= \overrightarrow{EP}QR + \overrightarrow{EQ}PR $.

Проделаем также для других векторов и получим выражение для $\overrightarrow{EQ}$:
$\overrightarrow{EQ}RS= \overrightarrow{ER}SQ + \overrightarrow{ES}RQ $.

Вот тут идеи остановились и началось рисование всяких, как мне показалось вспомогательных прямых и попытки найти решение через теорему Менелая. Я, пожалуй, эти построения воздержусь публиковать.
Хотелось бы узнать ваши идеи.
П.С. Есть вероятность, что все же решить задачу нельзя при данных входящих. Ранее в этом задачнике уже встречалась задача, где недостаточность входящих данных была более явной.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы) - отдельные обозначения стоит набрать как формулы, чтобы они выглядели так же, вектора стоит набирать так, чтобы стрелка была не только над первой буквой;
- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[nnosipov]

math.fi в сообщении #1520788 писал(а):

Есть вероятность, что все же решить задачу нельзя при данных входящих.

Нет, задача сформулирована корректно. Если она из задачника, то, скорее всего, там есть и ответ: если $(R-P)/(Q-R)=\lambda$, то $(S-P)/(Q-S)=-\lambda$.

[math.fi]

nnosipov в сообщении #1520849 писал(а):

math.fi в сообщении #1520788 писал(а):

Есть вероятность, что все же решить задачу нельзя при данных входящих.

Нет, задача сформулирована корректно. Если она из задачника, то, скорее всего, там есть и ответ: если $(R-P)/(Q-R)=\lambda$, то $(S-P)/(Q-S)=-\lambda$.

Почему так? Я этого просто не вижу

[nnosipov]

math.fi в сообщении #1520861 писал(а):

Почему так? Я этого просто не вижу

И я не вижу. Но если тупо вычислить, то получается вот так. Ответ совпадает с тем, что в задачнике?

[TOTAL]

math.fi в сообщении #1520788 писал(а):

Вот тут идеи остановились и

Остановились, но потом снова пошли. Считайте треугольник $EPQ$ прямоугольным равнобедренным. Через угол $REQ$ найдите всё что надо.

[Null]

math.fi в сообщении #1520861 писал(а):

Почему так? Я этого просто не вижу

Задача явно на двойное отношение 4 точек/прямых.

[math.fi]

math.fi в сообщении #1520861 писал(а):

nnosipov в сообщении #1520849 писал(а):

math.fi в сообщении #1520788 писал(а):

Есть вероятность, что все же решить задачу нельзя при данных входящих.

Нет, задача сформулирована корректно. Если она из задачника, то, скорее всего, там есть и ответ: если $(R-P)/(Q-R)=\lambda$, то $(S-P)/(Q-S)=-\lambda$.

Почему так? Я этого просто не вижу

Похоже я просто не умею "просто вычислить". Не покажите как?

[svv]

Тут всё зависит от того, знакомы ли Вы с понятием двойного отношения четвёрки точек, четвёрки прямых (и связью между ними), или нет.

[math.fi]

svv в сообщении #1520879 писал(а):

Тут всё зависит от того, знакомы ли Вы с понятием двойного отношения четвёрки точек, четвёрки прямых (и связью между ними), или нет.

Вообще не знаком. Но что-то мне подсказывает, что может быть тут как-то без специальных знаний можно обойтись, если нет, то накидайте ссылок.

[nnosipov]

math.fi в сообщении #1520878 писал(а):

Не покажите как?

Я имел в виду метод координат. Во-первых, можно считать параллелограмм квадратом, причем с вершинами в точках $A=(0,0)$, $B=(0,1)$ и т.д. Во-вторых, зададим точки $P=(0,k)$ и $H=(l,0)$ с помощью параметров $k$ и $l$. В-третьих, вычислим точки $Q$, $R$ и $S$ (то есть, выразим их через $k$ и $l$). Это примитивно, но довольно громоздко, если делать вручную (я использовал компьютер). После этого можно найти $(R-P)/(Q-R)=2k/l$ и $(S-P)/(Q-S)=-2k/l$.

[svv]

Я тоже решал методом координат. Аффинным преобразованием можно привести картинку к такому виду (прямоугольник составлен из двух квадратов):

Считаем $E$ началом координат, прямая $EQ$ абсцисса, прямая $EP$ ордината.
Так как $ER$ — биссектриса $PEQ$, то $PE:EQ=PR:RQ=\lambda$. Значит, при подходящем масштабе координаты точек $E(0,0), Q(1,0), P(0,\lambda)$.
После этого несложно написать уравнения синих прямых и найти абсциссу их точки пересечения.

[TOTAL]

Просто по теореме синусов находите
$PR=\dfrac{\tg\omega}{1+\tg\omega}, \; RQ=\dfrac{1}{1+\tg\omega}, \; QS=\dfrac{\tg\omega}{1-\tg\omega}$

[svv]

Просто найдите $x$ как абсциссу пересечения $y=\lambda(1-x)$ и $y=-x$. У меня проще.