Двойственность в булевой алгебре и не только

[juna]

Все это изначально понятно.
Получаем рекурентные соотношения для числителей и знаменателей вида $p_{n+1}=a p_{n}-p_{n-1}$ и $q_{n+1}=a q_{n}-q_{n-1}$ при разных начальных условиях.
Интреснее проследить, как ведут себя H-V последовательности для других иррациональностей.
Для примера возьмем разложение
$\frac{e-1}{2}=\frac{1}{1+\frac{1}{6+\frac{1}{10+\frac{1}{14+\frac{1}{16+...}}}}}$
Для подходящих дробей получаем H-V последовательности:
$\frac{6}{7}=VH^5$
$\frac{61}{71}=VH^6V^9$
$\frac{860}{1001}=VH^6V^{10}H^{13}$
$\frac{13821}{16087}=VH^6V^{10}H^{14}V^{15}$
$\frac{277280}{322741}=VH^6V^{10}H^{14}V^{16}H^{19}$
$\frac{6668541}{7761871}=VH^6V^{10}H^{14}V^{16}H^{20}V^{23}$
...
Видны закономерности - степени H-V как раз числа из разложения в цепную дробь, и только самая правая степень на единицу меньше, которая изменяется при следующем уточнении.
Замечу также, что в приведенном lisp-code функцию HV_To_Number лучше модифицировать, преобразовав рекурсивный процесс в итерационный:

(defun HV_To_Number (L) 
   (defun iter (result LL)
      (cond
         ((Null LL) result)
         ((eq (car LL) 'H) (iter (+ result 1) (cdr LL)))
         ((eq (car LL) 'V) (iter (/ result (+ result 1)) (cdr LL)))))
   (iter 1 (reverse L)))    

Поскольку квадратичные иррациональности разлагаются в периодическую цепную дробь, получаются степени H-V последовательностей, в общем случае H-V последовательность - это аналог разложения в цепную дробь.

[Свободный Художник]

Свободный Художник писал(а):

Свободный Художник писал(а):

Произведение $u$ двух элементов $x$ и $y$ можно определить как корень уравнения:
$(x \bullet 1) \circ (u \bullet y) = (x \circ u) \bullet (1 \circ y)$
При подстановке в указанное уравнение $u = xy$ обе его части оказываются равными выражению $\dfrac{y(x + 1)}{y + 1}$.

В частности, при $y = \overline{x}$ и $u = 1$ получаем универсальное тождество:
$(x \bullet 1) \circ (1 \bullet \overline{x}) = (x \circ 1) \bullet (1 \circ \overline{x})$.

В принципе, мы могли бы с самого начала добавить выделенный элемент $1$ в сигнатуру системы $\mathbf{Q^+}$ (или $\mathbf{R^+}$) и охарактеризовать его роль в системе при помощи указанного универсального тождества, рассматриваемого в качестве новой аксиомы.

Вот еще об этом тождестве, характеризующем $1$.
Если воспользоваться вспомогательной системой $\mathbf{RA}$:

Свободный Художник писал(а):

Для наглядной верификации кандидатов на тождества, истинные в системе $\mathbf{Q^+}$, можно предложить следующую вспомогательную систему $\mathbf{RA}$ (от “Rectangles Algebra”):
$\mathbf{RA} = \langle \, \mathrm{RA}, \bullet\,, \circ\,, \overline{\phantom{a}}, \parallel\; \rangle \,,$

которая приведена также здесь: http://www.px-pict.com/9/6/4/5.html,
то упомянутое тождество можно ассоциировать с известной конфигурацией из “геометрической алгебры”:
http://www.px-pict.com/7/3/1/11/1.html

В этом контексте тождество $(x \bullet 1) \circ (1 \bullet \overline{x}) = (x \circ 1) \bullet (1 \circ \overline{x})$ будет означать, что квадрат можно “собрать” из меньших квадратов и прямоугольников двумя двойственными способами, отвечающими правой и левой частям указанного тождества.

С использованием рассотренных ранее в этом топике операций $V$ и $H$, указанное тождество перепишется в следующем виде: $[H(x)] \circ [H(\overline{x})] = [V(x)] \bullet [V(\overline{x})]$.

Как отметил juna, тождество $(x \bullet 1) \circ (1 \bullet \overline{x}) = (x \circ 1) \bullet (1 \circ \overline{x})$ следует из приведенного им более общего тождества.

juna писал(а):

Ваше же тождество в более общем виде я уже приводил $(y \bullet z)\circ(\overline{y}\bullet \overline {z}})=(y\circ \overline{z})\bullet (\overline{y}\circ z)$.Возьмите $y=1,z=x$

[Свободный Художник]

Свободный Художник писал(а):

Профессор Снэйп писал(а):

Стало очень интересно: можно ли выразить обычное умножение $x \cdot y$ через $x \circ y$, $x \bullet y$ и $\overline{x}$? Вроде бы доказал, что нельзя.

Произведение $u$ двух элементов $x$ и $y$ можно определить как корень уравнения:
$(x \bullet 1) \circ (u \bullet y) = (x \circ u) \bullet (1 \circ y)$
При подстановке в указанное уравнение $u = xy$ обе его части оказываются равными выражению $\dfrac{y(x + 1)}{y + 1}$.

juna писал(а):

Речь идет о непредставимости умножения термом фиксированной длины.

И все же операция $\cdot$ умножения в системе $\mathbf{Q^+}$ определяется вполне стандартным образом (для первопорядковых теорий с равенством). Для краткости определим тернарный предикат $R(u, x, y)$:
$\forall u\forall x\forall y\{R(u, x, y) \equiv [(x \bullet 1) \circ (u \bullet y) = (x \circ u) \bullet (1 \circ y)]\}$.

Постулируем две аксиомы:
$\forall x\forall y\exists u R(u, x, y)$;
$\forall x\forall y\forall u_1\forall u_2 \{R(u_1, x, y) \& R(u_2, x, y) \Rightarrow (u_1 = u_2)\}$.

Введем новый бинарный функциональный символ $\cdot$ и добавим аксиому:
$\forall x\forall y R((x \cdot y), x, y)$,

После этого мы можем утверждать, что определили в системе $\mathbf{Q^+}$ операцию $\cdot$ умножения.

[juna]

Можно, конечно, сказать - подбирайте такое $u$, чтобы правая и левая часть указанного равенства совпадали, найденное $u$ будет произведением $xy$. Но, во-первых, надо показать, что равенство достигается при одном единственном $u=xy$, во-вторых это не так, в-третьих, посчитать $\dfrac{y(x + 1)}{y + 1}$ через введенные операции мы также не умеем.

[Свободный Художник]

juna писал(а):

Свободный Художник в сообщении #169546 писал(а):

Произведение $u$ двух элементов $x$ и $y$ можно определить как корень уравнения:
$(x \bullet 1) \circ (u \bullet y) = (x \circ u) \bullet (1 \circ y)$
При подстановке в указанное уравнение $u = xy$ обе его части оказываются равными выражению $\dfrac{y(x + 1)}{y + 1}$.

Можно, конечно, сказать - подбирайте такое $u$, чтобы правая и левая часть указанного равенства совпадали, найденное $u$ будет произведением $xy$. Но, во-первых, надо показать, что равенство достигается при одном единственном $u=xy$, во-вторых это не так, в-третьих, посчитать $\dfrac{y(x + 1)}{y + 1}$ через введенные операции мы также не умеем.

Вы можете привести пример таких двух конкретных рациональных чисел $x$ и $y$ для которых указанное уравнение имеет два различных корня?
Я конечно понимаю, что даже если Вы и не сможете привести такой пример, это все же еще не отменяет необходимости доказательства единственности. Так что оно за мной.
По поводу Вашего третьего возражения я сочиню отдельный пост.

[juna]

Свободный Художник писал(а):

Так что оно за мной..

Да, Вы оказались правы. У получающегося там квадратного уравнения $u^2-2yxu+y^2x^2=0$ нулевой дискриминант.
Значит решение однозначно, но построение остается неконструктивным.

[Свободный Художник]

juna писал(а):

Свободный Художник в сообщении #169546 писал(а):

Произведение $u$ двух элементов $x$ и $y$ можно определить как корень уравнения:
$(x \bullet 1) \circ (u \bullet y) = (x \circ u) \bullet (1 \circ y)$
При подстановке в указанное уравнение $u = xy$ обе его части оказываются равными выражению $\dfrac{y(x + 1)}{y + 1}$.

... в-третьих, посчитать $\dfrac{y(x + 1)}{y + 1}$ через введенные операции мы также не умеем.

Если провести аналогию с булевой алгеброй, то при ее аксиоматизации мы можем выбрать различные наборы операций в качестве основных.
Допустим, в системе $\mathbf{B}$ в качестве основных выбраны операции объединения и дополнения, а в системе $\mathbf{B_1}$ в качестве основных выбраны операции симметрической разности и пересечения.

Допустим, что для системы $\mathbf{B}$ аксиомы уже известны и мы желаем создать альтернативную аксиоматизацию для системы $\mathbf{B_1}$. В качестве некоторого промежуточного шага мы можем выразить основные операции системы $\mathbf{B_1}$ в виде некоторых термов, состоящих из основных операций системы $\mathbf{B}$ и затем, когда будем “нащупывать” истинные предложения для аксиоматизации системы $\mathbf{B_1}$, транслировать их в предложения системы $\mathbf{B}$ и верифицировать их там.

В свете этой аналогии, пусть система $\mathbf{Q^++}$ -- будет обычной системой положительных рациональных чисел с обычными операциями сложения, вычитания, умножения, деления, выбранных в качестве основных.
Наряду с ней мы можем рассмотеть некоторую систему $\mathbf{Q^+}$ с операциями $\bullet\,, \circ\,, \overline{\phantom{a}}$ и в ее рамках попытаться дать альтернативную аксиоматизацию системы положительных рациональных чисел.
При “нащупывании” кандидатов на роль аксиом системы $\mathbf{Q^+}$ мы можем транслировать их в соответствующие предложения системы $\mathbf{Q^++}$ и пытаться доказать их там.

Добавлено спустя 27 минут 26 секунд:

juna писал(а):

Свободный Художник писал(а):

Так что оно за мной..

Значит решение однозначно, но построение остается неконструктивным.

Насчет конструктивности судить не берусь, но, в принципе, это стандартный прием в мат. логике. Вот здесь выдержки из учебника Мендельсона по этому поводу:
http://www.px-pict.com/9/6/2/1.html

С формальной точки зрения я, кажется, сделал все правильно.

[juna]

Попадаем на цитату из вашей же ссылки: "общеизвестно, что такие определения хотя и удобны, но ничего нового к теории не добавляют."
Получили полиномиально проверяемое решение - для любых $x,y,u$ легко можем проверить $u=xy$ или нет. Вот если бы существовал полиномиальный алгоритм нахождения решения, а мы доказали, что его не существует, т.е. решили проблему $P\not =NP$
На самом деле операция умножения тривиально вводится через последовательное суммирование в нашей системе, но только в виде терма нефиксированной длины.

[Свободный Художник]

Тем не менее, иерархия определений в рамках некоторой теории обычно строится, поскольку, по-видимому, позволяет сделать теорию более понятной и хорошо структурированной.
С другой стороны, отнюдь не все определимо в данной теории (под “определимостью” будем понимать определимость в теориях первого порядка с равенством). Например, унарные операции $V$ и $H$, а также элемент $1$ определимы в $\mathbf{Q^+}$

Свободный Художник писал(а):

Например, для $\mathbf{Q^+}$ являются справедливыми, очевидно, следующие два утверждения:
(1) Существует элемент, удовлетворяющий условию $\overline{x} = x$;
(2) Такой элемент единственен.
Положив этому элементу естественное имя 1, мы можем определить две двойственные друг по отношению к другу унарные операции: $H(x) = x \bullet 1$ и $V(x) = x \circ 1$.

А вот элементы $0$ и $\infty$ -– не определимы в $\mathbf{Q^+}$, поэтому, если мы хотим говорить о них, то должны явно добавить их в сигнатуру системы, что, пользуясь случаем, я и делаю:

$\mathbf{Q^+_{\, 0, \infty}} = \langle \, \mathrm{Q^+}, \bullet\,, \circ\,, \overline{\phantom{a}}\,, 0\,, \infty \rangle$

И, естественно, добавить еще аксиомы вида:
$x \bullet 0 = x\,, \; x \circ \infty = x \,;$
$x \bullet \infty = \infty\,, \; x \circ 0 = 0 \,;$
$\overline{0} = \infty\,, \; \overline{\infty} = 0\,;$
Здесь мы действительно добавили “новое” в $\mathbf{Q^+}$, поэтому и $\mathbf{Q^+_{\, 0,\: \infty}}$ -- новая система по отношению к $\mathbf{Q^+}$.
-------------------------------

Итак, будем считать, что умножение в $\mathbf{Q^+}$ мы определили. Теперь мы в состоянии определить в $\mathbf{Q^+}$ еще две двойственные операции, которые ранее пробовались на роль основных (я буду писать $\blacksquare$ вместо $\bullet$ и $\square$ вместо $\circ$):

Профессор Снэйп писал(а):

juna писал(а):

Вы правы, так будет даже идемпотентность
$x \bullet y=\frac{x+y}{2}$

Да, при

$$ x \bullet y = \frac{x+y}{2} \text{ и } x \circ y = \frac{2xy}{x+y} $$

идемпотентность будет. Но дистрибутивности всё равно не будет :(

$x \,\blacksquare\, y = (x \bullet y) \cdot V(1)$;
$x \,\square\, y = (x \circ y) \cdot H(1)$.

$\blacksquare$ и $\square$ -- хорошие такие операции (арифметическое и гармоническое средние), которые, как мы видим, являются двойственными друг по отношению к другу в системе $\mathbf{Q^+}$.

[Свободный Художник]

juna писал(а):

Попадаем на цитату из вашей же ссылки: "общеизвестно, что такие определения хотя и удобны, но ничего нового к теории не добавляют."

Говоря о том, что “… ничего нового к теории не добавляют”, Мендельсон имел в виду, что такие определения не означают перехода к какой-то принципиально новой системе, отличной от исходной системы, в данном случае, от системы $\mathbf{Q^+}$. Т. е. здесь речь идет о “консервативном расширении сигнатуры исходной системы”, как иногда выражаются.
Если бы удалось, как пишет Профессор Снэйп:

Профессор Снэйп писал(а):

Стало очень интересно: можно ли выразить обычное умножение $x \cdot y$ через $x \circ y$, $x \bullet y$ и $\overline{x}$? Вроде бы доказал, что нельзя.

выразить умножение в виде некоторого терма конечной длины из основных операций $\bullet\,, \circ\,, \overline{\phantom{a}}$, то и в этом случае мы ничего нового к $\mathbf{Q^+}$ не добавили бы.

В системе $\mathbf{Q^+_{\, 0,\: \infty}}$ с использованием операций $\blacksquare$ и $\square$ арифметического и гармонического средних можно доказать следующий любопытный факт о Stern-Brocot Tree:

Свободный Художник писал(а):

Кстати говоря, система с двумя унарными операциями $V$ и $H$, основанная на системе $\mathbf{Q^+}$, также весьма интересна (обозначим ее $\mathbf{SBT}$):
$\mathbf{SBT} = \langle \, \mathrm{SBT}, V, H, 1 \rangle$,
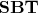
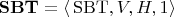
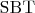
где $\mathrm{SBT}$ есть снова множество положительных рациональных чисел;
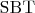
$V$ и $H$ есть унарные операции на множестве $\mathrm{SBT}$, определяемые как указано выше;
$1$ есть выделенный элемент во множестве $\mathrm{SBT}$.
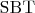
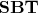
Во-первых, $\mathbf{SBT}$ есть абсолютно свободная алгебра с двумя унарными операциями и одним выделенным элементом;
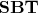
во-вторых, система $\mathbf{SBT}$ может служить основой для анализа различных соотношений, возникающих в контексте Stern-Brocot Tree:
http://mathworld.wolfram.com/Stern-BrocotTree.html
http://www.cut-the-knot.org/blue/Stern.shtml
http://en.wikipedia.org/wiki/Stern-Brocot_tree

Сперва сформулируем, потом докажем.
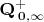
Поправим, кстати, определение системы $\mathbf{Q^+_{\, 0, \infty}}$. В качестве ее носителя, очевидно, должно быть указано множество $\mathrm{Q^+ \cup \{0, \infty \}}$, где $\mathrm{Q^+}$ по прежнему есть множество положительных рациональных чисел:

$\mathbf{Q^+_{\, 0, \infty}} = \langle \, \mathrm{Q^+ \cup \{0, \infty \}}, \bullet\,, \circ\,, \overline{\phantom{a}}\,, 0\,, \infty \rangle$.

Любопытный факт касается “закона роста” этого дерева.
Рассмотрим, например, 2-ой уровень Stern-Brocot Tree:
http://www.px-pict.com/10/4/4/2.html

На этом 2-м уровне находится, в частности, зеленое число $2/3$, расположенное между черными числами $1/2$ и $1/1$.
Зеленость числа $2/3$ означает, что оно возникло именно на 2-ом уровне Дерева, а окружающие его черные числа $1/2$ и $1/1$, между которыми оно вставилось, возникли на предыдущих уровнях.

На следующем 3-ем уровне Дерева число $2/3$ станет уже черным (ведь оно возникло на предыдущем уровне), а между ним и “еще более древним” черным числом $1/1$ вставится новый зеленый росточек –- число $3/4$.
Обозначим числа, о которых шла речь, буквами $N, A, M, B$:
$N = 1/2, A = 2/3, M = 3/4, B = 1/1$.
Очевидно, что они упорядочены по величине следующим образом: $N < A < M < B$.

Оказывается, что число $M$ вставляется между ранее построенными числами $A$ и $B$ таким образом, чтобы расстояние $NM$ было средним гармоническим расстояний $NA$ и $NB$. В виде формулы это запишется так:

$(M \blacktriangleright N) = ((A \blacktriangleright N) \,\square\, (B \blacktriangleright N))$,

где $\blacktriangleright$ есть операция вычитания, которую мы, очевидно, можем определить в системе $\mathbf{Q^+_{\, 0,\: \infty}}$.

Приведенная формула выражает “закон роста” левого поддерева.
Аналогичный “закон роста” для правого поддерева может быть выражен двойственной формулой:

$(M \vartriangleright N) = ((A \vartriangleright N) \,\blacksquare \, (B \vartriangleright N))$,

в которой фигурируют операция $\blacksquare$ арифметического среднего и операция $\vartriangleright$ “ко-вычитания” (т. е. операция, обратная операции $\circ$).

[Свободный Художник]

Свободный Художник писал(а):

Любопытный факт касается “закона роста” этого дерева.

Чтобы при формулировке “любопытного факта” не апеллировать к диаграмме с изображением Stern-Brocot Tree, можно ввести в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ понятие “интервала, ассоциированного с данным положительным рациональным числом $x$”.
С интуитивной точки зрения, это – интервал, который определяется двумя числами, между которыми на соответствующем уровне дерева вставляется положительное рациональное число $x$ при своем “возникновении”.
Например, для $x = 1/3$ ассоциированный интервал будет $(0, 1/2)$; для $x = 4/7$ – интервал $(1/2, 3/5)$; для $x = 5/1$ – интервал $(4/1, \infty)$ и т. д.

Формально этот интервал можно определить следующим образом. Пусть $\varphi$ будет произвольной строкой из символов $V$ и $H$ и пусть выражение $\varphi(x)$ будет обозначать соответствующий терм, составленный из символов операций $V$ и $H$; например, выражение $VHV(x)$ будет обозначать терм $V(H(V(x))$.

Каждому положительному рациональному числу $x$ соответствует единственная строка $\varphi$, определяемая из соотношения $x = \varphi(1)$. Если длина строки $\varphi$ равна $n$, то число $x$ возникает на $n$ - ом уровне дерева, вставляясь при этом, как можно показать, между числами $\varphi(0)$ и $\varphi(\infty)$, которые и определяют “интервал $(\varphi(0), \varphi(\infty))$, ассоциированный с данным положительным рациональным числом $x$”.

При вычислении выражений $\varphi(0)$ и $\varphi(\infty)$ можно использовать следующие соотношения:
$H(0) = 1, H(\infty) = \infty, V(0) = 0, V(\infty) = 1.$

[Свободный Художник]

Свободный Художник писал(а):

Свободный Художник писал(а):

Любопытный факт касается “закона роста” этого дерева.

Чтобы при формулировке “любопытного факта” не апеллировать к диаграмме с изображением Stern-Brocot Tree, можно ввести в системе $\mathbf{Q^+_{\, 0,\: \infty}}$ понятие “интервала, ассоциированного с данным положительным рациональным числом $x$”.

В свете вышесказанного, “закон роста” для левого поддерева можно сформулировать так (на левом поддереве расположены все рациональные числа, меньшие $1$).

Если длина строки $\varphi$ равна $n$, то тройка $\varphi(0), \varphi(1), \varphi(\infty)$ обозначает на диаграмме с изображением Stern-Brocot Tree ситуацию возникновения на $n$ - ом уровне дерева “зеленого росточка” $\varphi(1)$, вставленного между ранее построенными “черными” числами $\varphi(0)$ и $\varphi(\infty)$.

На следующем $(n+1)$ - ом уровне дерева между числами $\varphi(0)$ и $\varphi(1)$ вставится новое число $(\varphi V)(1)$, а между числами $\varphi(1)$ и $\varphi(\infty)$ -- новое число $(\varphi H)(1)$ ($\varphi H$ означает строку, полученную из строки $\varphi$ путем приписывания к ней справа символа $H$).
“Закон роста” выражает эти новые числа $(\varphi V)(1)$ и $(\varphi H)(1)$ как некоторую функцию от трех ранее возникших чисел $\varphi(0), \varphi(1), \varphi(\infty)$:

$(M \blacktriangleright N) = ((A \blacktriangleright N) \,\square\, (B \blacktriangleright N))$,
где $N = \varphi(0),\; A = \varphi(1),\; M = (\varphi H)(1),\; B = \varphi(\infty);$
$\square$ есть операция гармонического среднего; $\blacktriangleright$ есть операция вычитания.

$N, A, M, B$ есть гармоническая четверка точек, поскольку точка $M$ делит отрезок $AB$ “внутренним образом” в том же самом отношении, что и точка $N$ делит отрезок $AB$ “внешним образом”.

Аналогично: $(N \blacktriangleright M) = ((N \blacktriangleright A) \,\square\, (N \blacktriangleright B))$,
где $A = \varphi(0),\; M = (\varphi V)(1),\; B = \varphi(1),\; N = \varphi(\infty)$
(здесь точка $N$ “внешнего деления” расположена справа от отрезка $AB$.
-----------------------------

Для правого поддерева законы роста “переворачиваются” (на правом поддереве расположены все рациональные числа, большие $1$).

Если точка $N$ “внешнего деления” расположена справа от отрезка $AB$, то
$((B \vartriangleright N) \,\blacksquare \, (A \vartriangleright N)) = (M \vartriangleright N)$,
где $B = \varphi(0),\; M = (\varphi V)(1),\; A = \varphi(1),\; N = \varphi(\infty);$
$\blacksquare$ есть операция арифметического среднего; $\vartriangleright$ есть операция ко-вычитания.

Если точка $N$ “внешнего деления” расположена слева от отрезка $AB$, то
$(N \vartriangleright M) = ((N \vartriangleright B) \,\blacksquare \, (N \vartriangleright A))$,
где $N = \varphi(0),\; B = \varphi(1),\; M = (\varphi H)(1),\; A = \varphi(\infty).$

Операция ко-вычитания выражается через обычные операции следующим образом: если $x = a/b$ и $y = c/d$, то $x \vartriangleright y = \dfrac{ac}{bc - ad}$.
(т. е. ко-вычитать мы можем только из меньшего большее, тогда как вычитать – только из большего меньшее)
-----------------------------

На странице http://www.px-pict.com/10/4/4/4.html расположен калькулятор, в котором можно поэкспериментировать с приведенными выше соотношениями (калькулятор будет гарантированно работать в Internet Explorer). Нужно только в поле “Исходное число” ввести числитель и знаменатель исходного числа $x$; калькулятор сам посчитает все остальное, в частности, определит для $x$ строку $\varphi$, определяемую из условия $x = \varphi(1)$ (эта строка называется там “Программой числа $x$”).

[Свободный Художник]

Чтобы записать “законы роста” из предыдущего поста в виде универсальных предложений, нужно спустить фигурирующие там строки символов в алфавите $\{V, H\}$ с мета-уровня на объектный уровень.
Для этого естественно расширить систему $\mathbf{Q^+_{\, 0, \infty}}$, заставив действовать на ее множестве-носителе $\mathrm{Q^+_{\, 0, \infty}} = \mathrm{Q^+} \cup \{0, \infty \}$ свободную полугруппу строк
$\mathbf{S_{\, V, H}} = \langle \, \{V, H\}^+,\, \cdot \, \rangle$,
где $\{V, H\}^+$ есть множество всех строк в алфавите $\{V, H\}$,
$\cdot$ есть операция конкатенации строк (которую при записи термов будем, как правило, опускать).

Т. е. расширить систему $\mathbf{Q^+_{\, 0, \infty}}$ до системы
$\mathbf{SQ^+_{\, 0, \infty}} = \langle \, \mathbf{S_{\, V, H}} \, ,\, \mathbf{Q^+_{\, 0, \infty}}\,, \, * \, \rangle$,
где $*$ есть операция “действия”:
для любых чисел $x, y$, принадлежащих $\mathrm{Q^+_{\, 0,\: \infty}}$ и для любой строки $\varphi$, принадлежащей $\{V, H\}^+$,
запись $y = \varphi * x$ означает, что число $y$ является результатом действия строки $\varphi$ на число $x$.

Смысл операции $*$ действия определяется смыслом определенных в предыдущих постах операторов $V$ и $H$; например, если $x = 2/3$ и $\varphi = HV$, то $\varphi * x = HV*(2/3) = H(V(2/3)) = 7/5$.
Далее вместо $y = \varphi * x$ будем также писать $y = \varphi(x)$.

На множестве $\{V, H\}^+$ всех строк в алфавите $\{V, H\}$ можно определить и другие полезные операции. Например, операцию $Left(\varphi)$, сопоставляющую каждой строке $\varphi$ символ, стоящий на ее левом конце и операцию $Right(\varphi)$, сопоставляющую каждой строке $\varphi$ символ, стоящий на ее правом конце.
----------------------------

Теперь “законы роста” из предыдущего поста могут быть записаны в виде универсальных предложений в системе $\mathbf{SQ^+_{\, 0,\: \infty}}$. Например, самый первый “закон роста”:

$(M \blacktriangleright N) = ((A \blacktriangleright N) \,\square\, (B \blacktriangleright N))$,
где $N = \varphi(0),\; A = \varphi(1),\; M = (\varphi H)(1),\; B = \varphi(\infty);$
$\square$ есть операция гармонического среднего; $\blacktriangleright$ есть операция вычитания;
может быть записан в виде следующего универсального предложения:

$\forall \varphi \{(Left(\varphi) = V) \Rightarrow \{[(\varphi H)(1) \blacktriangleright \varphi(0)] = [[(\varphi(1) \blacktriangleright \varphi(0)] \,\square\, [\varphi(\infty) \blacktriangleright \varphi(0)]]\}\}$.
----------------------------

Систему, представляющую собой действие свободной полугруппы на некотором множестве часто называют “автоматом”:
http://en.wikipedia.org/wiki/Semigroup_action
http://en.wikipedia.org/wiki/Automata_theory
http://en.wikipedia.org/wiki/Semiautomaton

Так что арифметика рациональных чисел вполне может рассматриваться как раздел Computer Science :)
http://en.wikipedia.org/wiki/Computer_science
http://en.wikipedia.org/wiki/Theoretical_computer_science

[Профессор Снэйп]

Свободный Художник писал(а):

Так что арифметика рациональных чисел вполне может рассматриваться как раздел Computer Science

Думаю, к этому выводу можно было прийти и более простыми средствами

[juna]

О дереве Штерна-Брока написано также в "Конкретной математике", и пока мы почти не выходим за пределы описанного там. Мне бы было интересно построить это дерево на все $\mathbb Q$.