Надо с этим заканчивать. Напомню

. Система
![$\left\{\begin{matrix}
\left [ (KT+1)^2+(K+T)^2 \right ]\left [ (KT-1)^2+(K-T)^2 \right ]=\square \\
\left [ (KT+T)^2+(K-1)^2 \right ]\left [ (KT-T)^2+(K+1)^2 \right ]=\square
\end{matrix}\right.(4')$ $\left\{\begin{matrix}
\left [ (KT+1)^2+(K+T)^2 \right ]\left [ (KT-1)^2+(K-T)^2 \right ]=\square \\
\left [ (KT+T)^2+(K-1)^2 \right ]\left [ (KT-T)^2+(K+1)^2 \right ]=\square
\end{matrix}\right.(4')$](https://dxdy-03.korotkov.co.uk/f/2/c/b/2cb4ee054a0d4e428e1edc15be1df55582.png)
, а значит и
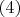
, сводятся в конечном итоге к уравнению

. Если верно последнее, то пара

,

удовлетворяет

и обращает тождество
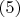
в решение сильного кубоида. Это согласуется также с выводом
Коровьева (поскольку

) и эквивалентно уравнению

, которым последнее время увлекся
Volik. Мне вот тоже показалось, что оно наиболее удачно разбивает проблему на кучу проблем, перепишем его так:

Видя равенство сумм четырех квадратов, приравняем почленно к тождеству Эйлера:




Пронумеруем мысленно скобочки с

-й по

-ю и далее с

-й по

-ю, и в том же порядке будем записывать в системы. Линейные системы решаются отлично. Неприятность в том, что параметры

оказываются в этом случае свободными аргументами, чего по понятным причинам быть не должно. Во всяком случае не все, и тут тупик. Сформулируем задачу так: переменные

должны быть таковы, чтобы соседние скобки давали в произведении единицу, причем две последние сами должны быть

. Тогда отношение соседних скобок окажутся квадратами искомых значений. Звучит обнадёживающе, но, действуя напрямую, сразу получаем систему квадратных уравнений по всем параметрам (я, кстати, не пробовал), а пробиваясь через разности квадратов, вынуждены после искать приравнивания к формам вида

, которые на деле оказываются никакими не

, а всё теми же

. Опять тупик. Ловушка Майи. Пробуем зайти сбоку. Рассмотрим полусуммы

-й и
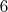
-й скобок:

Домножая на
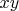
, имеем

(полусуммы

-й и

-й скобок)

По той же схеме

Домножая на


Получили два уравнения линейных относительно

Приравнивая решения одного и другого, имеем


Третья дробь образовалась сложением числителей и знаменателей двух предыдущих, что при равенстве дробей позволено. Обозначим сразу

, и перемножим крестиком элементы равных дробей:

Отсюда

и, наконец,

Вот на этом месте подобные инсинуации обычно и заканчиваются, но на этот раз повезло:

Это имеет общее решение. Полный список дальнейших перепетий опускаю, выкладываю замены, которые проверяются прямой подстановкой:

Из

следует

. Значения параметров

в новых терминах получаем из линейной подсистемы

-го и

-го уравнений, приравнивая к единице и подставляя новые значения переменных:


Новые значения

определены через

, каждый может выписать их для себя по желанию. Не пропустить ошибку на этом этапе вычислений в некотором смысле помогает сама задача: небольшая неточность тут же порождает выражение длиной в две строки, значит где-то косяк. Однако, подставляя новые выражения в первоначальную систему, получаем что-то уж слишком легкие выражения:

Замечу, что для

главное требование уже выполняется: произведение

-й и

-й скобок равно единице. Думаю, тут связь с

-м и

-м уравнениями, которые уже решены. Если так, то из оставшихся четырёх достаточно решить два, например два последних, которые подозрительно линейны относительно переменных

. Выпишу их отдельно, они того заслуживают.

Значит,

всё-таки придется брать свободной переменной. Из онлайн-сервисов один напрочь отказался это решать и стал раздавать благие советы, другой выдал решение с нулём. Пришлось пальчиками. Оказалось, записанная в строки система действительно имеет решение

Но, собирая ее обратно в дробь, получаем ноль в числителе и ноль в знаменателе. Более того, все дроби системы при при этой подстановке обрастают нулями. А определитель системы не ноль. Решение есть, оно такое:

. Однако, рациональное решение существует:

, такой вывод был бы доказательством. Но математика точная наука, имеем более осторожный вывод:
если существует общее решение уравнения  , то оно невыразимо тождеством Эйлера от восьми переменных
, то оно невыразимо тождеством Эйлера от восьми переменных. По-моему, на человеческий язык это переводится так: решений нет. Но кто знает... Добавлю, что никаких предположений, допущений или неполных решений по ходу дела не возникало. Чистая алгебра.



