===========ММ237=============== ММ237 (7 баллов)
Студент математического факультета Вася Пупкин написал на доске некоторую перестановку

из

в виде произведения независимых циклов (запись каждого цикла начинается с наименьшего элемента; опускались ли в записи циклы длины 1 - неизвестно). Васины однокурсники прокомментировали эту запись.
Аня:

– тождественная перестановка.
Ваня: Длины всех циклов

– числа Фибоначчи.
Даня: В

существует ровно 3 перестановки, квадрат которых равен

.
Маня: Хм, уравнение

не может иметь в

ровно 3 решения ни при каком

.
Саня: Более того, количество решений уравнения

в

не может быть нечетным ни при каком

.
Таня: Квадрат наибольшего элемента в самом длинном цикле меньше порядка

.
Зина:

имеет столько же циклов, сколько и

Лина: Внутри всех циклов элементы строго возрастают.
Нина: Произведение всех элементов одного из циклов кратно произведению всех элементов более длинного цикла и сумме всех элементов более короткого.
Фаина: Зина, Лина и Нина правы.
Вася (умница и отличник) заметил, что количество верных утверждений его однокурсников равно наибольшей длине цикла в

.
Найдите

.
РешениеПривожу решения Виктора Филимоненкова, Анатолия Казмерчука и vpb.
(Решение vpb)
Решение задачи ММ237. Имеет место такое
Предложение. Пусть  . Если длины циклов в
. Если длины циклов в  --- различные нечетные числа, то уравнение
--- различные нечетные числа, то уравнение  имеет ровно одно решение. Во всех остальных случаях решений или нет, или их четное число.
имеет ровно одно решение. Во всех остальных случаях решений или нет, или их четное число. (Доказательство этого предложения дадим в конце решения).
Отсюда сразу вытекает, что Даня и Саня неправы (рассмотрим элемент со структурой циклов

или

), а Маня права. Значит, среди всех утверждений не более 8 верных, и не менее 1.
Отметим, что если нет циклов длины 5, то Зина права, а иначе нет (при возведении в 5-ю степень цикл длины 5 пропадает, а цикл другой длины превращается в другой цикл той же длины).
Допустим, что есть 8 верных утверждений. Тогда все, кроме Дани и Сани, правы, значит

. С другой стороны, длина наибольшего цикла должна быть

, что противоречит

.
Допустим, что верных утверждений 7. Тогда длина наибольшего цикла --- 7, откуда

, и

также не есть число Фибоначчи, и поэтому Аня и Ваня неправы. Значит, верных утверждений не более 6, противоречие.
Допустим, верных утверждений не более 3. Тогда длина наибольшего цикла не более 3. Поэтому Аня, Ваня и Зина правы, а также и Маня, значит есть

верных утверждения, противоречие.
Итак, верных утверждений может быть 4, 5, или 6.
Рассмотрим возможность, когда верных утверждений 4, и, следовательно, наибольший цикл имеет длину 4. Очевидно, в этом случае Аня и Ваня неправы. Кроме того, порядок

не превосходит

. Но квадрат наибольшего элемента в любом 4-цикле

, поэтому Таня неправа. Зина же права. Следовательно, среди Лины, Нины и Фаины --- ровно двое правых. Но этого быть никак не может. Действительно, если Лина или Нина не правы, то и Фаина тоже неправа, значит среди них троих правых

. Если же Лина и Нина правы обе, то и Фаина права, значит правы все трое. Двух не получается ни при каком раскладе.
Теперь рассмотрим случай, когда верных утверждений 6. Тогда наибольший цикл --- длины 6. Значит, Ваня неправ, а Зина права. Заметим, что квадрат наибольшего элемента в 6-цикле всегда

. С другой стороны, элемент, содержащий 6-цикл, имеет порядок не более 12. Поэтому Таня неправа. Значит, все остальные, кроме Дани, Сани, Тани и Вани, правы. В частности,

. Поскольку Нина права, есть по крайней мере три различных длины цикла. Поэтому структура циклов есть

или

. Допустим, что

. Тогда произведение элементов из 2-цикла кратно произведению элементов из 6-цикла. Но первое из этих произведений

, а второе

, противоречие. Следовательно, структура циклов

. Теперь заметим, что произведение элементов в 3-цикле может быть

, только если его элементы суть

. Но тогда оставшийся цикл --- это

. Однако

не кратно

. Итак, случая, когда верных утверждений 6, быть тоже не может.
Таким образом, верных утверждений 5. Значит, Зина неправа, и Аня тоже. Поскольку Зина неправа, то и Фаина неправа. Все оставшиеся --- Ваня, Маня, Таня, Лина и Нина --- должны быть правы. Поэтому есть по крайней мере три различных длины цикла, и все длины циклов --- числа Фибоначчи. Значит, возможные структуры циклов суть

, или

, или

, или

. Квадрат наибольшего элемента в самом длинном цикле --- по крайней мере

, поэтому порядок перестановки

. Этому ограничению удовлетворяет только структура циклов

. Порядок в таком случае равен

, значит наибольший элемент в 5-цикле не превосходит

, значит 5-цикл содержит в точности элементы

.
Произведение всех элементов 3-цикла кратно

, и сумме двух элементов из 2-цикла. Это возможно, только если элементы в 3-цикле суть

, а в 2-цикле

. Наконец, ввиду условия, что в каждом цикле цифры возрастают, получаем

.
Ответ:

.
В заключение следует обосновать предложение. Прежде всего, если

--- элемент описанного специального вида, то довольно ясно, что квадратный корень из

единственен.
Допустим, что

не имеет такого вида. Покажем, что в этом случае уравнение

необходимо имеет четное число решений.
Прежде всего допустим, что порядок

четен. Тогда

--- элемент порядка 2. Очевидно, что

, и потому

, коммутирует с любым элементом

таким, что

. Поэтому для любого такого элемента

. Следовательно, множество всех

с

оказывается объединением смежных классов по подгруппе

, и потому имеет четный порядок.
Теперь пусть

нечетен. Тогда

содержит

циклов одной и той же нечетной длины. Отсюда следует, что существует элемент

такой, что

и

. Откуда, в свою очередь, видим, что порядок подгруппы

четен. (Отметим еще раз, что все искомые элементы

лежат в

.)
Рассмотрим элемент

, где

. Тогда

. Очевидно также, что

. Поэтому для любого

такого, что

элемент

удовлетворяет соотношению

. Наоборот, если

и

, то для

имеем

. Значит, искомые элементы

взаимно однозначно соответствуют элементам

таким, что

. Но таких элементов четное число,
в силу классической
теоремы Фробениуса:
Если  --- конечная группа, и
--- конечная группа, и  делит
делит 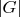 , то число решений уравнения
, то число решений уравнения  в
в  делится на
делится на  .
. (См.
М. Холл, Теория групп, гл.9, пар.1.)
(Конечно, предложение можно было бы доказать и более комбинаторными рассуждениями, специально приспособленными к группе

).
Обсуждение Естественно конкурсанты начали решение с проверки утверждений Мани и Сани, истинность которых не зависит от записанной на доске перестановки.
Причем проверка утверждения Мани оказывается наиболее сложной частью задачи. Некоторые участники предпочли ограничиться доказательством отсутствия трех решений уравнения

в

, другие же рассмотрели более общий вопрос о возможных количествах решений этого уравнения. Наконец, еще один участник привел чисто алгебраическое обоснование правоты Мани.
Ведущий пошел по пути "других" (комбинаторщиков), но для надежности проверил свои теоретические выкладки возведением всех элементов

в квадрат (разумеется, не руками). Конкурсанты оказались более уверенными в себе и к мощи компа не прибегали (некоторые - зря

).
Дальнейшие рассуждения практически все вели, перебирая возможные длины наибольшего цикла. И только Влад Франк отталкивался от истинности или ложности утверждения Фаины, показав, что этот путь тоже ведет к верному ответу.
Увлекшись обобщениями вопроса о количестве решений уравнения

в

, я доказал, что для любого простого

и любого

уравнение

имеет либо единственное решение, либо количество его решений кратно

(для составных показателей это уже не так).
Не остановившись на достигнутом, я вывел общую формулу для количества решений уравнения

в

(понятно, что ответ зависит от цикловой структуры

). Конечно, я понимал, что вряд ли являюсь первопроходцем: уж больно классический объект и слишком естественна постановка задачи. Но всерьез гуглить начал лишь только получив результат. Разумеется, у меня нашлись предшественники. Причем, насколько мне удалось установить, первая работа с ответом на этот вопрос была на русском языке (хотя я старательно формулировал запрос на английском):
http://www.mathnet.ru/php/archive.phtml ... n_lang=engПриведу все возможные количества решений

в

для небольших

и

.
k = 2
1 {1}
2 {0, 2}
3 {0, 1, 4}
4 {0, 1, 2, 10}
5 {0, 1, 2, 26}
6 {0, 1, 4, 76}
7 {0, 1, 2, 4, 8, 10, 232}
8 {0, 1, 2, 4, 8, 12, 20, 26, 764}
9 {0, 1, 2, 4, 10, 12, 16, 52, 76, 2620}
10 {0, 1, 2, 4, 6, 8, 10, 24, 26, 40, 152, 232, 9496}
k = 3
1 {1}
2 {1}
3 {0, 1, 3}
4 {0, 1, 9}
5 {0, 1, 3, 21}
6 {0, 1, 9, 81}
7 {0, 1, 3, 9, 21, 351}
8 {0, 1, 3, 9, 33, 81, 1233}
9 {0, 1, 3, 9, 18, 21, 27, 33, 351, 5769}
10 {0, 1, 3, 9, 18, 21, 33, 81, 1233, 31041}
k = 4
1 {1}
2 {0, 2}
3 {0, 1, 4}
4 {0, 1, 16}
5 {0, 1, 2, 56}
6 {0, 1, 4, 256}
7 {0, 1, 2, 4, 16, 1072}
8 {0, 1, 4, 8, 48, 56, 6224}
9 {0, 1, 2, 10, 16, 256, 33616}
10 {0, 1, 2, 4, 6, 10, 56, 64, 96, 1072, 218656}
k = 5
1 {1}
2 {1}
3 {1}
4 {1}
5 {0, 1, 25}
6 {0, 1, 145}
7 {0, 1, 25, 505}
8 {0, 1, 25, 145, 1345}
9 {0, 1, 25, 145, 505, 3025}
10 {0, 1, 25, 145, 385, 505, 1345, 78625}
k = 6
1 {1}
2 {0, 2}
3 {0, 6}
4 {0, 2, 18}
5 {0, 1, 2, 66}
6 {0, 1, 4, 396}
7 {0, 1, 2, 12, 2052}
8 {0, 1, 4, 6, 12, 36, 12636}
9 {0, 2, 4, 12, 18, 132, 91548}
10 {0, 2, 6, 8, 18, 24, 66, 792, 625176}
Поясню, как я реагировал на ошибки при подсчете возможных количеств решений уравнения

в

.
Фатальная ошибка (вместо самих решений считалось лишь возможное количество их цикловых видов), приведшая к "опровержению" утверждения Маши, разумеется, нарушила весь дальнейший ход решения и была отражена в оценке.
Автору неверных комбинаторных формул при подсчете количеств решений повезло больше. Одно решение при этом не исчезло, а три не появилось. Поэтому дальнейшая цепочка рассуждений привела к верному ответу. Но оставить ошибки на промежуточных шагах без внимания я, конечно, не мог.
Наконец, локальные арифметические ошибки, не повлиявшие на решения я вовсе не учитывал. Пример такой ошибки есть в приведенном решения Анатолия Казмерчука (там, где у Анатолия получилсь 18 решений должно быть 24). В самом деле, 18 получается как сумма двух слагаемых, одно из которых подсчитано верно и равно 12. Понятно, что сумма при этом будет больше 3, что собственно и требовалось. Поэтому данная вычислительная ошибка в принципе не могла повлиять на ход решения.
Неполный балл у Константина Шамсудтинова связан не с ошибками, а с недостаточно подробным изложением решения. Обосновав верную оценку утверждений Сани и Мани, Константин написал, что дальнейшее очевидно и привел правильный ответ.
Закончу разбор выражением удовлетворения содержательным обсуждением предыдущей задачи и сожаления, что эта увлеченность помешала участникам диалога обратить внимание на нынешнюю.
НаградыЗа решение задачи ММ237 участники Марафона получают следующие призовые баллы:
Анатолий Казмерчук - 10;
vpb - 8;
Виктор Филимоненков - 7;
Владислав Франк - 7;
Константин Шамсутдинов - 6.
Валентина Колыбасова - 5;
Евгений Гужавин - 2;
Эстетическая оценка задачи - 4.8 балла



