Пока тут затишье, хотелось бы прояснить некоторые моменты (более простые).
Итак, уравнения ОТО записываются для слабых полей при фиксированной
фоновой геометрии (Минковского) в гармонических координатах согласно Вайнбергу таким образом:
(У Вайнберга в главе 10. (Гравитация и Космология) (10.1.10))


Где

метрика Минковского,
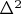
- Даламбертиан.
Гармонические координаты дают 4 дополнительных условия:

Что будет если:
1. Отказаться от гармонических условий
2. Отказаться от предположения слабого поля
3. отказаться от фиксированной фоновой метрики
4. отказаться вообще от фоновой метрики
Мои предположения:
1. Отказ от гармонических координат приведет к более сложному виду уравнений
для гравитаицонной волны . У Вайнберга (10.1.4).Это ведет к усложнению при численных расчетах.
2. Отказ от слабого поля ведет к нелинейным уравнениям.
3. Отказ от фиксированной фоновой метрики ведет к неоднозначности в решениях уравнений.
В частности неоднозначной величины потерь массы на излучение в виде гравитационной
энергии при слиянии черных дыр.
4. Отказ от фоновой метрики полностью ведет к работе с псевдотензором
энергии-импульса гравитационного поля и к разным результатам для таких расчетов и даже
к зависимости от системы координат.
В связи с этим хотелось бы понять, какие условия необходимы для работы с псевдотензором ,
уже как с тензором энергии гравитационного поля. Статья Грищука меня как-то сбила с толку
А также , что значит ввести в последнем четвертом случае понятия гравитон, если мы остаемся только
с обычной римановой геометрией?
Кто-нибудь разбирался с этими вопросами?



