warlock66613, да оно как бы честное в каком-то смысле (чисто технических ошибок в выкладках нет), но в то же самое время оно может быть совершенно не правильное, вот пример со слабой плоской гравитационной волной:

Считаем функцию

зависящей только от разности

. Вычисляем тензор Эйнштейна, для отличных от нуля компонент получаем:

Уравнения ОТО

Никакой волны нет, это пространство Минковского.
Теперь произносим заклинание:
рассмотрим слабую волну! Слабую - значит квадратичными членами пренебрегаем. Но если пренебречь квадратичными членами, то тензор Эйнштейна в этом приближении будет равен нулю (он же квадратичен по

), а раз так, то в линейном приближении в качестве функции

можно взять всё что угодно, хоть синус.
Только вот есть одна беда, такую слабую волну экспериментально обнаружить
никогда не удасться, уж больно она слаба...
В этом примере ведущий член разложения оказался квадратичный, а значит мы не имели права ограничиваться в разложении одними лишь линейными членами.
Простой пример

Один корень известен


Ищем другой корень в окрестности

, пишем

и раскладываем

Чтобы получить правильный ответ для (1) придётся разложить не до линейных, и даже не до квадратичных, а до кубических членов. Если ограничится линейным или даже квадратичным членом, то ответ будет не правильным.
-- 26.01.2017, 12:43 --Как вы собираетесь работать с энергией (псевдоэнергией) гравитационного поля и получить численный результат - 5 процентов после слияния черных дыр теряется на излучение в виде волн?
Решение уравнений ОТО описывающее слияние двух чёрных дыр не известно. Оценка в

взята, видимо, с потолка.
Как вычислить, могу лишь гадать, можно например взять и сравнить гравитационный радиус получившегося объекта (при
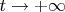
) с арифметической суммой гравитационных радиусов исходных объектов (при

). Но это так, из того что первое приходит в голову. Правильный ответ станет известен наверное не сильно раньше чем станет известно соответствующее решение.