Нас будет интересовать одна трактовка 4-го Предложения 7-ой книги "Начал":
http://www.px-pict.com/7/3/1/1/4/2/7/2/23.htmlиз "которого впоследствии развилась характерная для греческой математики теория отношений и пропорций".
... Два измерения позволяют естественным образом визуализировать расслоение пространства
элементарных звучий:
http://www.px-pict.com/9/6/8/2/2/3.htmlгде в качестве расслаивающего отображения выступает функция, реализуемая калькулятором из пункта 1 со страницы:
http://www.px-pict.com/10/4/4/1.htmlЯ буду использовать стандартную терминологию для расслоений, которая приведена, например, здесь:
http://www.px-pict.com/9/4/6/1/2/1.htmlhttp://www.px-pict.com/9/4/5.html-- Чт янв 21, 2016 23:53:58 --Значит, пространством расслоения будет множество всех упорядоченных пар натуральных чисел, а его базой -- множество все строк в алфавите из двух символов
и
, о котором я уже писал здесь:
Чтобы записать “законы роста” из предыдущего поста в виде универсальных предложений, нужно спустить фигурирующие там строки символов в алфавите
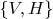
с мета-уровня на объектный уровень.
Для этого естественно расширить систему
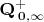
, заставив действовать на ее множестве-носителе
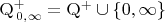
свободную полугруппу строк
,
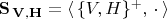
где
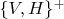
есть множество всех строк в алфавите
,
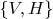
есть операция конкатенации строк (которую при записи термов будем, как правило, опускать).
Тогда мы могли бы сказать в духе Аристотеля, что две упорядоченные пары натуральных чисел пропорциональны тогда и только тогда, когда они имеют один и тот же антанаиресис.
http://www.px-pict.com/7/3/1/14/2/6/3/3.html
над субдоминантами 
очевиден. 
не традиционной в наше время высоте 
, а высоте 
, которая не только в центре стандартной клавиатуры, но и загадочным образом выполняет миссию центра симметрии расположения чёрно-белых клавиш.![$
\left\{\begin{matrix}
{\color[rgb]{.2,.7,.0}^{\theta6f{:}}_{\mathrm{{:}10T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta6g{:}}_{\mathrm{{:}7Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}6a{:}}_{\mathrm{{:}3TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.7,.4,.0}^{\theta6b{:}}_{\mathrm{{:}T3D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta6c{:}}_{\mathrm{{:}8T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta6d{:}}_{\mathrm{{:}5T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta6e{:}}_{\mathrm{{:}2T2D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta5f{:}}_{\mathrm{{:}9T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta5g{:}}_{\mathrm{{:}6Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}5a{:}}_{\mathrm{{:}2TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.7,.4,.0}^{\theta5b{:}}_{\mathrm{{:}3D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta5c{:}}_{\mathrm{{:}7T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta5d{:}}_{\mathrm{{:}4T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta5e{:}}_{\mathrm{{:}T2D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta4f{:}}_{\mathrm{{:}8T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta4g{:}}_{\mathrm{{:}5Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}4a{:}}_{\mathrm{{:}TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta4c{:}}_{\mathrm{{:}6T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta4d{:}}_{\mathrm{{:}3T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta4e{:}}_{\mathrm{{:}2D\o}}
\\
{\color[rgb]{.2,.7,.0}^{\theta3f{:}}_{\mathrm{{:}7T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta3g{:}}_{\mathrm{{:}4Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}4a{:}}_{\mathrm{{:}T3D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta3c{:}}_{\mathrm{{:}5T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta3d{:}}_{\mathrm{{:}2T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta2f{:}}_{\mathrm{{:}6T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta2g{:}}_{\mathrm{{:}3Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}2a{:}}_{\mathrm{{:}D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta2c{:}}_{\mathrm{{:}4T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta2d{:}}_{\mathrm{{:}T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta1f{:}}_{\mathrm{{:}5T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta1g{:}}_{\mathrm{{:}2Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta1c{:}}_{\mathrm{{:}3T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\Theta1d{:}}_{\mathrm{{:}\O\o}}}
\\
{\color[rgb]{.2,.7,.0}^{\theta\mbox{-}f{:}}_{\mathrm{{:}4T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta\mbox{-}g{:}}_{\mathrm{{:}Td}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta\mbox{-}c{:}}_{\mathrm{{:}2T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta\mbox{-}F{:}}_{\mathrm{{:}3T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta\mbox{-}G{:}}_{\mathrm{{:}\O d}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta\mbox{-}C{:}}_{\mathrm{{:}T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta1F{:}}_{\mathrm{{:}2Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta1C{:}}_{\mathrm{{:}\O2d}}}
\\
{\color[rgb]{.2,.7,.0}^{\theta2F{:}}_{\mathrm{{:}T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
\\
{\color[rgb]{.2,.7,.0}^{\theta3F{:}}_{\mathrm{{:}\O3d}}}
\end{matrix}\right\}
$](https://dxdy-02.korotkov.co.uk/f/5/c/a/5ca9219fb4a640c4f5f925432e76be3082.png "$
\left\{\begin{matrix}
{\color[rgb]{.2,.7,.0}^{\theta6f{:}}_{\mathrm{{:}10T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta6g{:}}_{\mathrm{{:}7Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}6a{:}}_{\mathrm{{:}3TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.7,.4,.0}^{\theta6b{:}}_{\mathrm{{:}T3D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta6c{:}}_{\mathrm{{:}8T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta6d{:}}_{\mathrm{{:}5T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta6e{:}}_{\mathrm{{:}2T2D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta5f{:}}_{\mathrm{{:}9T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta5g{:}}_{\mathrm{{:}6Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}5a{:}}_{\mathrm{{:}2TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.7,.4,.0}^{\theta5b{:}}_{\mathrm{{:}3D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta5c{:}}_{\mathrm{{:}7T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta5d{:}}_{\mathrm{{:}4T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta5e{:}}_{\mathrm{{:}T2D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta4f{:}}_{\mathrm{{:}8T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta4g{:}}_{\mathrm{{:}5Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}4a{:}}_{\mathrm{{:}TD\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta4c{:}}_{\mathrm{{:}6T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta4d{:}}_{\mathrm{{:}3T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.6,.4,.0}^{\theta4e{:}}_{\mathrm{{:}2D\o}}
\\
{\color[rgb]{.2,.7,.0}^{\theta3f{:}}_{\mathrm{{:}7T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta3g{:}}_{\mathrm{{:}4Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}4a{:}}_{\mathrm{{:}T3D\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta3c{:}}_{\mathrm{{:}5T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta3d{:}}_{\mathrm{{:}2T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta2f{:}}_{\mathrm{{:}6T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta2g{:}}_{\mathrm{{:}3Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.5,.4,.0}^{{\pitchfork}2a{:}}_{\mathrm{{:}D\o}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta2c{:}}_{\mathrm{{:}4T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\theta2d{:}}_{\mathrm{{:}T\o}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta1f{:}}_{\mathrm{{:}5T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta1g{:}}_{\mathrm{{:}2Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta1c{:}}_{\mathrm{{:}3T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.4,.0}^{\Theta1d{:}}_{\mathrm{{:}\O\o}}}
\\
{\color[rgb]{.2,.7,.0}^{\theta\mbox{-}f{:}}_{\mathrm{{:}4T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta\mbox{-}g{:}}_{\mathrm{{:}Td}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta\mbox{-}c{:}}_{\mathrm{{:}2T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta\mbox{-}F{:}}_{\mathrm{{:}3T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.4,.5,.0}^{\theta\mbox{-}G{:}}_{\mathrm{{:}\O d}}}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta\mbox{-}C{:}}_{\mathrm{{:}T2d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
{\color[rgb]{.2,.7,.0}^{\theta1F{:}}_{\mathrm{{:}2Td}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
_{~~ ~~ ~~\downarrow(\mathrm{{:}Td})\leftarrow}
&{\color[rgb]{.3,.6,.0}^{\theta1C{:}}_{\mathrm{{:}\O2d}}}
\\
{\color[rgb]{.2,.7,.0}^{\theta2F{:}}_{\mathrm{{:}T3d}}}
&^{\to(\mathrm{{:}Dt})\uparrow~~ ~~ ~~}
\\
\\
{\color[rgb]{.2,.7,.0}^{\theta3F{:}}_{\mathrm{{:}\O3d}}}
\end{matrix}\right\}
$")
![$
\left\{\begin{matrix}
{\color[rgb]{.5,.4,.0}{\pitchfork}5a\mathrm{{:}2TD\o}}
&{\color[rgb]{.7,.4,.0}\theta5b\mathrm{{:}3D\o}}
&{\color[rgb]{.3,.6,.0}\theta6c\mathrm{{:}8T2d}}
&{\color[rgb]{.4,.4,.0}\theta6d\mathrm{{:}5T\o}}
&{\color[rgb]{.6,.4,.0}\theta6e\mathrm{{:}2T2D\o}}
&{\color[rgb]{.2,.7,.0}\theta6f\mathrm{{:}10T3d}}
&{\color[rgb]{.4,.5,.0}\theta6g\mathrm{{:}7Td}}
\\
\mathrm{\color[rgb]{.5,.4,.0}I{:}[3^1/2^{-2}]}
&\mathrm{\color[rgb]{.7,.4,.0}II{:}[3^3/2^0]}
&\mathrm{\color[rgb]{.3,.6,.0}III{:}[2^8/3^2]}
&\mathrm{\color[rgb]{.4,.4,.0}IV{:}[2^5/3^0]}
&\mathrm{\color[rgb]{.6,.4,.0}V{:}[3^2/2^{-2}]}
&\mathrm{\color[rgb]{.2,.7,.0}VI{:}[2^{10}/3^3]}
&\mathrm{\color[rgb]{.4,.5,.0}VII{:}[2^7/3^1]}
\end{matrix}\right\}
$](https://dxdy-04.korotkov.co.uk/f/b/0/6/b06f8d5ba58dee187e7efb3124db198f82.png "$
\left\{\begin{matrix}
{\color[rgb]{.5,.4,.0}{\pitchfork}5a\mathrm{{:}2TD\o}}
&{\color[rgb]{.7,.4,.0}\theta5b\mathrm{{:}3D\o}}
&{\color[rgb]{.3,.6,.0}\theta6c\mathrm{{:}8T2d}}
&{\color[rgb]{.4,.4,.0}\theta6d\mathrm{{:}5T\o}}
&{\color[rgb]{.6,.4,.0}\theta6e\mathrm{{:}2T2D\o}}
&{\color[rgb]{.2,.7,.0}\theta6f\mathrm{{:}10T3d}}
&{\color[rgb]{.4,.5,.0}\theta6g\mathrm{{:}7Td}}
\\
\mathrm{\color[rgb]{.5,.4,.0}I{:}[3^1/2^{-2}]}
&\mathrm{\color[rgb]{.7,.4,.0}II{:}[3^3/2^0]}
&\mathrm{\color[rgb]{.3,.6,.0}III{:}[2^8/3^2]}
&\mathrm{\color[rgb]{.4,.4,.0}IV{:}[2^5/3^0]}
&\mathrm{\color[rgb]{.6,.4,.0}V{:}[3^2/2^{-2}]}
&\mathrm{\color[rgb]{.2,.7,.0}VI{:}[2^{10}/3^3]}
&\mathrm{\color[rgb]{.4,.5,.0}VII{:}[2^7/3^1]}
\end{matrix}\right\}
$")
![$\left\{
\begin{matrix}
\mathrm{S_{n}}
&\equiv
&{\alpha_1}\mathrm{S}_{p_1}
&{\alpha_2}\mathrm{S}_{p_2}
&\dots
&{\alpha_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n
&=
&p_1^{\alpha_1}
&p_2^{\alpha_2}
&\cdots
&p_k^{\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{\alpha_i}
\\
\end{matrix}
\right.
$](https://dxdy-04.korotkov.co.uk/f/f/3/6/f36134d1dddb4cf8904bf22adcb33f4082.png "$\left\{
\begin{matrix}
\mathrm{S_{n}}
&\equiv
&{\alpha_1}\mathrm{S}_{p_1}
&{\alpha_2}\mathrm{S}_{p_2}
&\dots
&{\alpha_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n
&=
&p_1^{\alpha_1}
&p_2^{\alpha_2}
&\cdots
&p_k^{\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{\alpha_i}
\\
\end{matrix}
\right.
$")
![-- $\mathbf{\mbox{[]}}$](https://dxdy-01.korotkov.co.uk/f/8/5/1/85154731a0aba0b0ba8944e157742b9582.png "-- $\mathbf{\mbox{[]}}$")
символизируют приписываниие без пробела.
вотчину собственного субсонанта 
:![$\left\{
\begin{matrix}
\mathrm{S_{n}}
&\equiv
&{\alpha_1}\mathrm{S}_{p_1}
&{\alpha_2}\mathrm{S}_{p_2}
&\dots
&{\alpha_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n
&=
&p_1^{\alpha_1}
&p_2^{\alpha_2}
&\cdots
&p_k^{\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n^{-1}
&=
&p_1^{-\alpha_1}
&p_2^{-\alpha_2}
&\cdots
&p_k^{-\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{-\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
\mathrm{s}_n
&\equiv
&{\alpha_1}\mathrm{s}_{p_1}
&{\alpha_2}\mathrm{s}_{p_2}
&\dots
&{\alpha_k}\mathrm{s}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
\\
\end{matrix}
\right.
$](https://dxdy-01.korotkov.co.uk/f/c/b/1/cb1dd7ec79d11c308aacf067b882bdab82.png "$\left\{
\begin{matrix}
\mathrm{S_{n}}
&\equiv
&{\alpha_1}\mathrm{S}_{p_1}
&{\alpha_2}\mathrm{S}_{p_2}
&\dots
&{\alpha_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n
&=
&p_1^{\alpha_1}
&p_2^{\alpha_2}
&\cdots
&p_k^{\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n^{-1}
&=
&p_1^{-\alpha_1}
&p_2^{-\alpha_2}
&\cdots
&p_k^{-\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{-\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
\mathrm{s}_n
&\equiv
&{\alpha_1}\mathrm{s}_{p_1}
&{\alpha_2}\mathrm{s}_{p_2}
&\dots
&{\alpha_k}\mathrm{s}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
\\
\end{matrix}
\right.
$")
![$\left\{
\begin{matrix}
\mathrm{S_{m}}
&\equiv
&{\beta_1}\mathrm{S}_{p_1}
&{\beta_2}\mathrm{S}_{p_2}
&\dots
&{\beta_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\beta_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
m
&=
&p_1^{\beta_1}
&p_2^{\beta_2}
&\cdots
&p_k^{\beta_k}
&=
&\prod_{i=1}^{k}p_i^{\beta_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n^{-1}
&=
&p_1^{-\alpha_1}
&p_2^{-\alpha_2}
&\cdots
&p_k^{-\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{-\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
\mathrm{s}_n
&\equiv
&{\alpha_1}\mathrm{s}_{p_1}
&{\alpha_2}\mathrm{s}_{p_2}
&\dots
&{\alpha_k}\mathrm{s}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
\\
\end{matrix}
\right.
$](https://dxdy-04.korotkov.co.uk/f/7/e/9/7e94fa3c67667d5a52f7277560b4a01082.png "$\left\{
\begin{matrix}
\mathrm{S_{m}}
&\equiv
&{\beta_1}\mathrm{S}_{p_1}
&{\beta_2}\mathrm{S}_{p_2}
&\dots
&{\beta_k}\mathrm{S}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\beta_i}\mathrm{S}_{p_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
m
&=
&p_1^{\beta_1}
&p_2^{\beta_2}
&\cdots
&p_k^{\beta_k}
&=
&\prod_{i=1}^{k}p_i^{\beta_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
n^{-1}
&=
&p_1^{-\alpha_1}
&p_2^{-\alpha_2}
&\cdots
&p_k^{-\alpha_k}
&=
&\prod_{i=1}^{k}p_i^{-\alpha_i}
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
\mathrm{s}_n
&\equiv
&{\alpha_1}\mathrm{s}_{p_1}
&{\alpha_2}\mathrm{s}_{p_2}
&\dots
&{\alpha_k}\mathrm{s}_{p_k}
&\equiv
&\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
\\
\end{matrix}
\right.
$")
![$
{:}\mathrm{S_{m}}[m/n]s_n\equiv\mathbf{\mbox{[]}}_{i=1}^{k}{\beta_i}\mathrm{S}_{p_i}[\prod_{i=1}^{k}p_i^{\beta_i}/\prod_{i=1}^{k}p_i^{\alpha_i}]\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
$](https://dxdy-02.korotkov.co.uk/f/d/f/8/df8a0f864be3e24fafd439da7016fe7682.png "$
{:}\mathrm{S_{m}}[m/n]s_n\equiv\mathbf{\mbox{[]}}_{i=1}^{k}{\beta_i}\mathrm{S}_{p_i}[\prod_{i=1}^{k}p_i^{\beta_i}/\prod_{i=1}^{k}p_i^{\alpha_i}]\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i}
$")
, например, то брикет рассыпается на множество всех сочетаний 
в системе 
:![$\left\{
\begin{matrix}
:
&:
&:
&:
\\
\begin{matrix}
\mathbf{{:}2T\o\equiv S_{4}[4/1]s_{1}\equiv}\\
\equiv\mathrm{2T0D[\frac{2^{2}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3Tt\equiv S_{8}[8/2]s_{2}\equiv}\\
\equiv\mathrm{3T0D[\frac{2^{3}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2TDd\equiv S_{12}[12/3]s_{3}\equiv}\\
\equiv\mathrm{2T1D[2^{2}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}4T2t\equiv S_{16}[16/4]s_{4}\equiv}\\
\equiv\mathrm{4T0D[2^{4}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&\begin{matrix}
\begin{xy}*{[7/2]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\end{matrix}
&\begin{matrix}
\begin{xy}*{[11/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[10/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[15/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[14/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[13/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
\begin{matrix}
\mathbf{{:}D\o\equiv S_{3}[3/1]s_{1}\equiv}\\
\equiv\mathrm{0T1D[\frac{2^{0}{\cdot}3^{1}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}TDt\equiv S_{6}[6/2]s_{2}\equiv}\\
\equiv\mathrm{1T1D[\frac{2^{1}{\cdot}3^{1}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2Dd\equiv S_{9}[9/3]s_{3}\equiv}\\
\equiv\mathrm{0T2D[2^{0}{\cdot}3^{2}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2TD2t\equiv S_{12}[12/4]s_{4}\equiv}\\
\equiv\mathrm{2T1D[2^{2}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&\begin{matrix}\\
\begin{xy}*{[5/2]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3Td\equiv S_{8}[8/3]s_{3}\equiv}\\
\equiv\mathrm{3T0D[2^{3}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[11/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[10/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
&
&\begin{matrix}
\begin{xy}*{[7/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\\\\\
\end{matrix}
&\begin{matrix}
\mathbf{{:}2D2t\equiv S_{9}[9/4]s_{4}\equiv}\\
\equiv\mathrm{0T2D[2^{0}{\cdot}3^{2}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
\begin{matrix}
\mathbf{{:}T\o\equiv S_{2}[2/1]s_{1}\equiv}\\
\equiv\mathrm{1T0D[\frac{2^{1}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2Tt\equiv S_{4}[4/2]s_{2}\equiv}\\
\equiv\mathrm{2T0D[\frac{2^{2}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}TDd\equiv S_{6}[6/3]s_{3}\equiv}\\
\equiv\mathrm{1T1D[2^{1}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3T2t\equiv S_{8}[8/4]s_{4}\equiv}\\
\equiv\mathrm{3T0D[2^{3}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}\\
\begin{xy}*{[5/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[7/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\end{matrix}
\\
&\begin{matrix}
\mathbf{{:}Dt\equiv S_{3}[3/2]s_{2}\equiv}\\
\equiv\mathrm{0T1D[\frac{2^{0}{\cdot}3^{1}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&
&\begin{matrix}
\mathbf{{:}TD2t\equiv S_{6}[6/4]s_{4}\equiv}\\
\equiv\mathrm{1T1D[2^{1}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}
\mathbf{{:}2Td\equiv S_{4}[4/3]s_{3}\equiv}\\
\equiv\mathrm{2T0D[2^{2}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}\\
\begin{xy}*{[5/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
&
&
&
\\
\begin{matrix}
\mathbf{{:}\O\o\equiv S_{1}[1/1]s_{1}\equiv}\\
\equiv\mathrm{0T0D[\frac{2^{0}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}Tt\equiv S_{2}[2/2]s_{2}\equiv}\\
\equiv\mathrm{1T0D[\frac{2^{1}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}Dd\equiv S_{3}[3/3]s_{3}\equiv}\\
\equiv\mathrm{0T1D[2^{0}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2T2t\equiv S_{4}[4/4]s_{4}\equiv}\\
\equiv\mathrm{2T0D[2^{2}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&
&
\\
&
&
&\begin{matrix}
\mathbf{{:}D2t\equiv S_{3}[3/4]s_{4}\equiv}\\
\equiv\mathrm{0T1D[2^{0}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}
\mathbf{{:}Td\equiv S_{2}[2/3]s_{3}\equiv}\\
\equiv\mathrm{1T0D[2^{1}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&
\\
&
&
&
\\
&\begin{matrix}
\mathbf{{:}\O t\equiv S_{1}[1/2]s_{2}\equiv}\\
\equiv\mathrm{0T0D[\frac{2^{0}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&
&\begin{matrix}
\mathbf{{:}T2t\equiv S_{2}[2/4]s_{4}\equiv}\\
\equiv\mathrm{1T0D[2^{1}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&
&
\\
&
&
&
\\
&
&\begin{matrix}
\mathbf{{:}\O d\equiv S_{1}[1/3]s_{3}\equiv}\\
\equiv\mathrm{0T0D[2^{0}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&
\\
&
&
&
\\
&
&
&\begin{matrix}
\mathbf{{:}\O2t\equiv S_{1}[1/4]s_{4}\equiv}\\
\equiv\mathrm{0T0D[2^{0}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
\end{matrix}
\right\}
$](https://dxdy-02.korotkov.co.uk/f/d/a/1/da1d59dca0adbe4a40cf827d9397c73582.png "$\left\{
\begin{matrix}
:
&:
&:
&:
\\
\begin{matrix}
\mathbf{{:}2T\o\equiv S_{4}[4/1]s_{1}\equiv}\\
\equiv\mathrm{2T0D[\frac{2^{2}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3Tt\equiv S_{8}[8/2]s_{2}\equiv}\\
\equiv\mathrm{3T0D[\frac{2^{3}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2TDd\equiv S_{12}[12/3]s_{3}\equiv}\\
\equiv\mathrm{2T1D[2^{2}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}4T2t\equiv S_{16}[16/4]s_{4}\equiv}\\
\equiv\mathrm{4T0D[2^{4}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&\begin{matrix}
\begin{xy}*{[7/2]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\end{matrix}
&\begin{matrix}
\begin{xy}*{[11/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[10/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[15/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[14/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[13/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
\begin{matrix}
\mathbf{{:}D\o\equiv S_{3}[3/1]s_{1}\equiv}\\
\equiv\mathrm{0T1D[\frac{2^{0}{\cdot}3^{1}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}TDt\equiv S_{6}[6/2]s_{2}\equiv}\\
\equiv\mathrm{1T1D[\frac{2^{1}{\cdot}3^{1}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2Dd\equiv S_{9}[9/3]s_{3}\equiv}\\
\equiv\mathrm{0T2D[2^{0}{\cdot}3^{2}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2TD2t\equiv S_{12}[12/4]s_{4}\equiv}\\
\equiv\mathrm{2T1D[2^{2}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&\begin{matrix}\\
\begin{xy}*{[5/2]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3Td\equiv S_{8}[8/3]s_{3}\equiv}\\
\equiv\mathrm{3T0D[2^{3}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[11/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\begin{xy}*{[10/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
&
&\begin{matrix}
\begin{xy}*{[7/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\\\\\
\end{matrix}
&\begin{matrix}
\mathbf{{:}2D2t\equiv S_{9}[9/4]s_{4}\equiv}\\
\equiv\mathrm{0T2D[2^{0}{\cdot}3^{2}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
\begin{matrix}
\mathbf{{:}T\o\equiv S_{2}[2/1]s_{1}\equiv}\\
\equiv\mathrm{1T0D[\frac{2^{1}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2Tt\equiv S_{4}[4/2]s_{2}\equiv}\\
\equiv\mathrm{2T0D[\frac{2^{2}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}TDd\equiv S_{6}[6/3]s_{3}\equiv}\\
\equiv\mathrm{1T1D[2^{1}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}3T2t\equiv S_{8}[8/4]s_{4}\equiv}\\
\equiv\mathrm{3T0D[2^{3}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}\\
\begin{xy}*{[5/3]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
&\begin{matrix}
\begin{xy}*{[7/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}\\
\end{matrix}
\\
&\begin{matrix}
\mathbf{{:}Dt\equiv S_{3}[3/2]s_{2}\equiv}\\
\equiv\mathrm{0T1D[\frac{2^{0}{\cdot}3^{1}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&
&\begin{matrix}
\mathbf{{:}TD2t\equiv S_{6}[6/4]s_{4}\equiv}\\
\equiv\mathrm{1T1D[2^{1}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}
\mathbf{{:}2Td\equiv S_{4}[4/3]s_{3}\equiv}\\
\equiv\mathrm{2T0D[2^{2}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}\\
\begin{xy}*{[5/4]}@+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
\end{matrix}
\\
&
&
&
\\
\begin{matrix}
\mathbf{{:}\O\o\equiv S_{1}[1/1]s_{1}\equiv}\\
\equiv\mathrm{0T0D[\frac{2^{0}{\cdot}3^{0}}{3^{0}{\cdot}2^{0}}]0d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}Tt\equiv S_{2}[2/2]s_{2}\equiv}\\
\equiv\mathrm{1T0D[\frac{2^{1}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}Dd\equiv S_{3}[3/3]s_{3}\equiv}\\
\equiv\mathrm{0T1D[2^{0}{\cdot}3^{1}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&\begin{matrix}
\mathbf{{:}2T2t\equiv S_{4}[4/4]s_{4}\equiv}\\
\equiv\mathrm{2T0D[2^{2}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&
&
\\
&
&
&\begin{matrix}
\mathbf{{:}D2t\equiv S_{3}[3/4]s_{4}\equiv}\\
\equiv\mathrm{0T1D[2^{0}{\cdot}3^{1}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&\begin{matrix}
\mathbf{{:}Td\equiv S_{2}[2/3]s_{3}\equiv}\\
\equiv\mathrm{1T0D[2^{1}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&
\\
&
&
&
\\
&\begin{matrix}
\mathbf{{:}\O t\equiv S_{1}[1/2]s_{2}\equiv}\\
\equiv\mathrm{0T0D[\frac{2^{0}{\cdot}3^{0}}{3^{0}{\cdot}2^{1}}]0d1t}
\end{matrix}
&
&\begin{matrix}
\mathbf{{:}T2t\equiv S_{2}[2/4]s_{4}\equiv}\\
\equiv\mathrm{1T0D[2^{1}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
&
&
&
\\
&
&
&
\\
&
&\begin{matrix}
\mathbf{{:}\O d\equiv S_{1}[1/3]s_{3}\equiv}\\
\equiv\mathrm{0T0D[2^{0}{\cdot}3^{0}/3^{1}{\cdot}2^{0}]1d0t}
\end{matrix}
&
\\
&
&
&
\\
&
&
&\begin{matrix}
\mathbf{{:}\O2t\equiv S_{1}[1/4]s_{4}\equiv}\\
\equiv\mathrm{0T0D[2^{0}{\cdot}3^{0}/3^{0}{\cdot}2^{2}]0d2t}
\end{matrix}
\\
\end{matrix}
\right\}
$")
. Стали законными все сочетания 
:![$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&.\cdot
\\
\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0m0d0t}}}
{\mathbf{{:}T\o\equiv^{S_{2}[2/}_{/1]s_{1}}}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}2Tt\equiv^{S_{4}[4/}_{/2]s_{2}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}TDd\equiv^{S_{6}[6/}_{/3]s_{3}}}}}
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}3T2t\equiv^{S_{8}[8/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TMm\equiv^{S_{10}[10/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{2T1D0M}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2TDdt\equiv^{S_{12}[12/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\begin{xy}*{\mathrm{S_{7}[7/4]s_{4}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2Dm\equiv^{S_{9}[9/}_{/5]s_{5}}}}}
&\begin{xy}*{\mathrm{S_{11}[11/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}Md\equiv^{S_{5}[5/}_{/3]s_{3}}}}}
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}3Tm\equiv^{S_{8}[8/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TMdt\equiv^{S_{10}[10/}_{/6]s_{6}}}}}
&..
\\
\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}Dt\equiv^{S_{3}[3/}_{/2]s_{2}}}}}
&\square
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}TD2t\equiv^{S_{6}[6/}_{/4]s_{4}}}}}
&\begin{xy}*{\mathrm{S_{7}[7/5]s_{5}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2Ddt\equiv^{S_{9}[9/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}2Td\equiv^{S_{4}[4/}_{/3]s_{3}}}}}
&\square
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}3Tdt\equiv^{S_{8}[8/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}M2t\equiv^{S_{5}[5/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TDm\equiv^{S_{6}[6/}_{/5]s_{5}}}}}
&\begin{xy}*{\mathrm{S_{7}[7/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0m0d0t}}}
{\mathbf{{:}\O\o\equiv^{S_{1}[1/}_{/1]s_{1}}}}}
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}Tt\equiv^{S_{2}[2/}_{/2]s_{2}}}}}
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}Dd\equiv^{S_{3}[3/}_{/3]s_{3}}}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}2T2t\equiv^{S_{4}[4/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}Mm\equiv^{S_{5}[5/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TDdt\equiv^{S_{6}[6/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2Tm\equiv^{S_{4}[4/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}Mdt\equiv^{S_{5}[5/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}D2t\equiv^{S_{3}[3/}_{/4]s_{4}}}}}
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2Tdt\equiv^{S_{4}[4/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}Dm\equiv^{S_{3}[3/}_{/5]s_{5}}}}}
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}\O t\equiv^{S_{1}[1/}_{/2]s_{2}}}}}
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}T2t\equiv^{S_{2}[3/}_{/4]s_{4}}}}}
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}Ddt\equiv^{S_{3}[3/}_{/6]s_{6}}}}}
&..
\end{matrix}\right\}
$](https://dxdy-04.korotkov.co.uk/f/f/8/0/f80d7f138f99b3af0fe2bc0fb9365f4882.png "$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&.\cdot
\\
\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0m0d0t}}}
{\mathbf{{:}T\o\equiv^{S_{2}[2/}_{/1]s_{1}}}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}2Tt\equiv^{S_{4}[4/}_{/2]s_{2}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}TDd\equiv^{S_{6}[6/}_{/3]s_{3}}}}}
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}3T2t\equiv^{S_{8}[8/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TMm\equiv^{S_{10}[10/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{2T1D0M}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2TDdt\equiv^{S_{12}[12/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\begin{xy}*{\mathrm{S_{7}[7/4]s_{4}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2Dm\equiv^{S_{9}[9/}_{/5]s_{5}}}}}
&\begin{xy}*{\mathrm{S_{11}[11/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}Md\equiv^{S_{5}[5/}_{/3]s_{3}}}}}
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}3Tm\equiv^{S_{8}[8/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TMdt\equiv^{S_{10}[10/}_{/6]s_{6}}}}}
&..
\\
\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}Dt\equiv^{S_{3}[3/}_{/2]s_{2}}}}}
&\square
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}TD2t\equiv^{S_{6}[6/}_{/4]s_{4}}}}}
&\begin{xy}*{\mathrm{S_{7}[7/5]s_{5}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2Ddt\equiv^{S_{9}[9/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}2Td\equiv^{S_{4}[4/}_{/3]s_{3}}}}}
&\square
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}3Tdt\equiv^{S_{8}[8/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}M2t\equiv^{S_{5}[5/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TDm\equiv^{S_{6}[6/}_{/5]s_{5}}}}}
&\begin{xy}*{\mathrm{S_{7}[7/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0m0d0t}}}
{\mathbf{{:}\O\o\equiv^{S_{1}[1/}_{/1]s_{1}}}}}
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}Tt\equiv^{S_{2}[2/}_{/2]s_{2}}}}}
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}Dd\equiv^{S_{3}[3/}_{/3]s_{3}}}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}2T2t\equiv^{S_{4}[4/}_{/4]s_{4}}}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}Mm\equiv^{S_{5}[5/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TDdt\equiv^{S_{6}[6/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2Tm\equiv^{S_{4}[4/}_{/5]s_{5}}}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}Mdt\equiv^{S_{5}[5/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}D2t\equiv^{S_{3}[3/}_{/4]s_{4}}}}}
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2Tdt\equiv^{S_{4}[4/}_{/6]s_{6}}}}}
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}Dm\equiv^{S_{3}[3/}_{/5]s_{5}}}}}
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}\O t\equiv^{S_{1}[1/}_{/2]s_{2}}}}}
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}T2t\equiv^{S_{2}[3/}_{/4]s_{4}}}}}
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}Ddt\equiv^{S_{3}[3/}_{/6]s_{6}}}}}
&..
\end{matrix}\right\}
$")
, тоже может отображаться в музыкальном пространстве: 
множество допустимых музыкальных выразительностей расширяется до всех сочетаний 
![$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&:
&.\cdot
\\
\overset{\mathrm{^{1T0D0M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0q0m0d0t}}}
{\mathbf{{:}T[2/1]\o}}}
&\overset{\mathrm{^{2T0D0M0Q}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0q0m0d1t}}}
{\mathbf{{:}2T[4/2]t}}}
&\overset{\mathrm{^{1T1D0M0Q}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0q0m1d0t}}}
{\mathbf{{:}TD[6/3]d}}}
&\overset{\mathrm{^{3T0D0M0Q}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0q0m0d2t}}}
{\mathbf{{:}3T[8/4]2t}}}
&\overset{\mathrm{^{1T0D1M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}TMm}}}
&\overset{\mathrm{^{2T1D0M0Q}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0q0m1d1t}}}
{\mathbf{{:}2TDdt}}}
&\overset{\mathrm{^{1T0D0M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TQq}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0q0m0d2t}}}
{\mathbf{{:}Q[7/4]2t}}}
&\overset{\mathrm{^{0T2D0M0Q}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}2D[9/5]m}}}
&\begin{xy}*{\mathrm{S_{11}[11/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\begin{xy}*{\mathrm{S_{13}[13/7]s_{7}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}M[5/3]d}}}
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}3T[8/5]m}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TMdt}}}
&\overset{\mathrm{^{2T1D0M0Q}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}2TDq}}}
&..
\\
\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}D[3/2]t}}}
&\square
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}TD[6/4]2t}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}Q[7/5]m}}}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2D[9/6]dt}}}
&\begin{xy}*{\mathrm{S_{11}[11/7]s_{7}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}2T[4/3]d}}}
&\square
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}3T[8/6]dt}}}
&\overset{\mathrm{^{1T0D1M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TMq}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}M[5/4]2t}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TD[6/5]m}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0q0m1d1t}}}
{\mathbf{{:}Q[7/6]dt}}}
&\overset{\mathrm{^{0T2D0M0Q}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}2D[9/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{^{3T0D0M0Q}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}3T[8/7]q}}}
&..
\\
\overset{\mathrm{^{0T0D0M0Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0q0m0d0t}}}
{\mathbf{{:}\O[1/1]\o}}}
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}T[2/2]t}}}
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}D[3/3]d}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}2T[4/4]2t}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}M[5/5]m}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TD[6/6]dt}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}Q[7/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2T[4/5]m}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}M[5/6]dt}}}
&\overset{\mathrm{^{1T1D0M0Q}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TD[6/7]q}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}D[3/4]2t}}}
&\square
&\square
&\square
&..
\\
\square
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}T[2/3]d}}}
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2T[4/6]dt}}}
&\overset{\mathrm{^{0T0D1M0Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}M[5/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}D[3/5]m}}}
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{2T0D0M0Q}}
{\underset{\mathrm{1q0m0d0t}}
{\mathbf{{:}2T[4/7]q}}}
&..
\\
\square
&\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}\O[1/2]t}}}
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}T[2/4]2t}}}
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}D[3/6]dt}}}
&\square
&..
\\
&
&:
&:
&:
&:
&:
&\cdot.
\end{matrix}\right\}
$](https://dxdy-02.korotkov.co.uk/f/9/9/c/99c2d29e26b7353ddfc5b211607d1a2e82.png "$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&:
&.\cdot
\\
\overset{\mathrm{^{1T0D0M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0q0m0d0t}}}
{\mathbf{{:}T[2/1]\o}}}
&\overset{\mathrm{^{2T0D0M0Q}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0q0m0d1t}}}
{\mathbf{{:}2T[4/2]t}}}
&\overset{\mathrm{^{1T1D0M0Q}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0q0m1d0t}}}
{\mathbf{{:}TD[6/3]d}}}
&\overset{\mathrm{^{3T0D0M0Q}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0q0m0d2t}}}
{\mathbf{{:}3T[8/4]2t}}}
&\overset{\mathrm{^{1T0D1M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}TMm}}}
&\overset{\mathrm{^{2T1D0M0Q}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0q0m1d1t}}}
{\mathbf{{:}2TDdt}}}
&\overset{\mathrm{^{1T0D0M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TQq}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0q0m0d2t}}}
{\mathbf{{:}Q[7/4]2t}}}
&\overset{\mathrm{^{0T2D0M0Q}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}2D[9/5]m}}}
&\begin{xy}*{\mathrm{S_{11}[11/6]s_{6}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&\begin{xy}*{\mathrm{S_{13}[13/7]s_{7}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}M[5/3]d}}}
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}3T[8/5]m}}}
&\overset{\mathrm{^{1T0D1M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TMdt}}}
&\overset{\mathrm{^{2T1D0M0Q}_{[2^{2}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}2TDq}}}
&..
\\
\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}D[3/2]t}}}
&\square
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}TD[6/4]2t}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{0q1m0d0t}}}
{\mathbf{{:}Q[7/5]m}}}
&\overset{\mathrm{^{0T2D0M}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2D[9/6]dt}}}
&\begin{xy}*{\mathrm{S_{11}[11/7]s_{7}}} @+;p+LD;+UR**h@{-};s0+RD;s0+UL**h@{-}\end{xy}
&..
\\
\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}2T[4/3]d}}}
&\square
&\square
&\overset{\mathrm{^{3T0D0M}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}3T[8/6]dt}}}
&\overset{\mathrm{^{1T0D1M0Q}_{[2^{1}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TMq}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}M[5/4]2t}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}TD[6/5]m}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0q0m1d1t}}}
{\mathbf{{:}Q[7/6]dt}}}
&\overset{\mathrm{^{0T2D0M0Q}_{[2^{0}{\cdot}3^{2}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}2D[9/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{^{3T0D0M0Q}_{[2^{3}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}3T[8/7]q}}}
&..
\\
\overset{\mathrm{^{0T0D0M0Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{0}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{0q0m0d0t}}}
{\mathbf{{:}\O[1/1]\o}}}
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}T[2/2]t}}}
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}D[3/3]d}}}
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}2T[4/4]2t}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}M[5/5]m}}}
&\overset{\mathrm{^{1T1D0M}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}TD[6/6]dt}}}
&\overset{\mathrm{^{0T0D0M1Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}{\cdot}7^{1}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}Q[7/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}2T[4/5]m}}}
&\overset{\mathrm{^{0T0D1M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}M[5/6]dt}}}
&\overset{\mathrm{^{1T1D0M0Q}_{[2^{1}{\cdot}3^{1}{\cdot}5^{0}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}TD[6/7]q}}}
&..
\\
\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}D[3/4]2t}}}
&\square
&\square
&\square
&..
\\
\square
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{0}]}_{0m1d0t}}}
{\mathbf{{:}T[2/3]d}}}
&\square
&\square
&\overset{\mathrm{^{2T0D0M}_{[2^{2}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}2T[4/6]dt}}}
&\overset{\mathrm{^{0T0D1M0Q}_{[2^{0}{\cdot}3^{0}{\cdot}5^{1}{\cdot}7^{0}/}}}
{\underset{\mathrm{^{/7^{1}{\cdot}5^{0}{\cdot}3^{0}{\cdot}2^{0}]}_{1q0m0d0t}}}
{\mathbf{{:}M[5/7]q}}}
&..
\\
\square
&\square
&\square
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{1}{\cdot}3^{0}{\cdot}2^{0}]}_{1m0d0t}}}
{\mathbf{{:}D[3/5]m}}}
&\square
&\square
&..
\\
\square
&\square
&\square
&\square
&\square
&\square
&\overset{\mathrm{2T0D0M0Q}}
{\underset{\mathrm{1q0m0d0t}}
{\mathbf{{:}2T[4/7]q}}}
&..
\\
\square
&\overset{\mathrm{^{0T0D0M}_{[2^{0}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{1}]}_{0m0d1t}}}
{\mathbf{{:}\O[1/2]t}}}
&\square
&\overset{\mathrm{^{1T0D0M}_{[2^{1}{\cdot}3^{0}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{0}{\cdot}2^{2}]}_{0m0d2t}}}
{\mathbf{{:}T[2/4]2t}}}
&\square
&\overset{\mathrm{^{0T1D0M}_{[2^{0}{\cdot}3^{1}{\cdot}5^{0}/}}}
{\underset{\mathrm{^{/5^{0}{\cdot}3^{1}{\cdot}2^{1}]}_{0m1d1t}}}
{\mathbf{{:}D[3/6]dt}}}
&\square
&..
\\
&
&:
&:
&:
&:
&:
&\cdot.
\end{matrix}\right\}
$")
, например, получается следующее выражение:![$
{:}\mathrm{S_{m}}[m/n]s_n\equiv{\beta_1}\mathrm{S_2}{\beta_2}\mathrm{S_3}{\beta_3}\mathrm{S_5}{\beta_4}\mathrm{S_7}{\beta_5}\mathrm{S_{11}}{\beta_6}\mathrm{S_{13}}{\beta_7}\mathrm{S_{17}}{\beta_8}\mathrm{S_{19}}{\beta_9}\mathrm{S_{23}}
[\prod_{i=1}^{k=9}p_i^{\beta_i}/
/\prod_{i=1}^{k=9}p_i^{\alpha_i}]
{\alpha_9}\mathrm{s_{23}}{\alpha_8}\mathrm{s_{19}}{\alpha_7}\mathrm{s_{17}}{\alpha_6}\mathrm{s_{13}}{\alpha_5}\mathrm{s_{11}}{\alpha_4}\mathrm{s_{7}}{\alpha_3}\mathrm{s_{5}}{\alpha_2}\mathrm{s_{3}}{\alpha_1}\mathrm{s_{2}}
$](https://dxdy-04.korotkov.co.uk/f/b/5/4/b5411a76a7554517d03c1551d177db2a82.png "$
{:}\mathrm{S_{m}}[m/n]s_n\equiv{\beta_1}\mathrm{S_2}{\beta_2}\mathrm{S_3}{\beta_3}\mathrm{S_5}{\beta_4}\mathrm{S_7}{\beta_5}\mathrm{S_{11}}{\beta_6}\mathrm{S_{13}}{\beta_7}\mathrm{S_{17}}{\beta_8}\mathrm{S_{19}}{\beta_9}\mathrm{S_{23}}
[\prod_{i=1}^{k=9}p_i^{\beta_i}/
/\prod_{i=1}^{k=9}p_i^{\alpha_i}]
{\alpha_9}\mathrm{s_{23}}{\alpha_8}\mathrm{s_{19}}{\alpha_7}\mathrm{s_{17}}{\alpha_6}\mathrm{s_{13}}{\alpha_5}\mathrm{s_{11}}{\alpha_4}\mathrm{s_{7}}{\alpha_3}\mathrm{s_{5}}{\alpha_2}\mathrm{s_{3}}{\alpha_1}\mathrm{s_{2}}
$")
![$\left\{\left\{
\begin{matrix}
\mathrm{\O}\\
\updownarrow\\
\mathbf{\mbox{[]}}_{i=1}^{k}{(\beta_i{=}0)}\mathrm{S}_{p_i}\\
\updownarrow\\
\prod_{i=1}^{k}p_i^{\beta_i=0}\\
\uparrow\\
p_0{=}1\\
\downarrow\\
\prod_{i=1}^{k}p_i^{-\alpha_i=0}\\
\updownarrow\\
\mathbf{\mbox{[]}}_{i=1}^{k}{(\alpha_i{=}0)}\mathrm{s}_{p_i}\\
\updownarrow\\
\mathrm{\o}
\end{matrix}
\right\}\right.
\left.
\begin{matrix}
{\beta_1}\mathrm{T}
&{\beta_2}\mathrm{D}
&{\beta_3}\mathrm{M}
&{\beta_4}\mathrm{Q}
&{\beta_5}\mathrm{N}
&{\beta_6}\mathrm{R}
&{\beta_7}\mathrm{P}
&{\beta_8}\mathrm{U}
&{\beta_9}\mathrm{V}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\beta_1}\mathrm{S}_{2}
&{\beta_2}\mathrm{S}_{3}
&{\beta_3}\mathrm{S}_{5}
&{\beta_4}\mathrm{S}_{7}
&{\beta_5}\mathrm{S}_{11}
&{\beta_6}\mathrm{S}_{13}
&{\beta_7}\mathrm{S}_{17}
&{\beta_8}\mathrm{S}_{19}
&{\beta_9}\mathrm{S}_{23}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
2^{\beta_1}
&3^{\beta_2}
&5^{\beta_3}
&7^{\beta_4}
&11^{\beta_5}
&13^{\beta_6}
&17^{\beta_7}
&19^{\beta_8}
&23^{\beta_9}
&\cdots
\\
\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
\\
p_1{=}2
&p_2{=}3
&p_3{=}5
&p_4{=}7
&p_5{=}11
&p_6{=}13
&p_7{=}17
&p_8{=}19
&p_9{=}23
&\cdots
\\
\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
\\
2^{-\alpha_1}
&3^{-\alpha_2}
&5^{-\alpha_3}
&7^{-\alpha_4}
&11^{-\alpha_5}
&13^{-\alpha_6}
&17^{-\alpha_7}
&19^{-\alpha_8}
&23^{-\alpha_9}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\alpha_1}\mathrm{s}_{2}
&{\alpha_2}\mathrm{s}_{3}
&{\alpha_3}\mathrm{s}_{5}
&{\alpha_4}\mathrm{s}_{7}
&{\alpha_5}\mathrm{s}_{11}
&{\alpha_6}\mathrm{s}_{13}
&{\alpha_7}\mathrm{s}_{17}
&{\alpha_8}\mathrm{s}_{19}
&{\alpha_9}\mathrm{s}_{23}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\alpha_1}\mathrm{t}
&{\alpha_2}\mathrm{d}
&{\alpha_3}\mathrm{m}
&{\alpha_4}\mathrm{q}
&{\alpha_5}\mathrm{n}
&{\alpha_6}\mathrm{r}
&{\alpha_7}\mathrm{p}
&{\alpha_8}\mathrm{u}
&{\alpha_9}\mathrm{v}
&\cdots
\end{matrix}
\right\}
$](https://dxdy-01.korotkov.co.uk/f/8/0/3/803ad89186e1caedb0825398bc8a32cf82.png "$\left\{\left\{
\begin{matrix}
\mathrm{\O}\\
\updownarrow\\
\mathbf{\mbox{[]}}_{i=1}^{k}{(\beta_i{=}0)}\mathrm{S}_{p_i}\\
\updownarrow\\
\prod_{i=1}^{k}p_i^{\beta_i=0}\\
\uparrow\\
p_0{=}1\\
\downarrow\\
\prod_{i=1}^{k}p_i^{-\alpha_i=0}\\
\updownarrow\\
\mathbf{\mbox{[]}}_{i=1}^{k}{(\alpha_i{=}0)}\mathrm{s}_{p_i}\\
\updownarrow\\
\mathrm{\o}
\end{matrix}
\right\}\right.
\left.
\begin{matrix}
{\beta_1}\mathrm{T}
&{\beta_2}\mathrm{D}
&{\beta_3}\mathrm{M}
&{\beta_4}\mathrm{Q}
&{\beta_5}\mathrm{N}
&{\beta_6}\mathrm{R}
&{\beta_7}\mathrm{P}
&{\beta_8}\mathrm{U}
&{\beta_9}\mathrm{V}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\beta_1}\mathrm{S}_{2}
&{\beta_2}\mathrm{S}_{3}
&{\beta_3}\mathrm{S}_{5}
&{\beta_4}\mathrm{S}_{7}
&{\beta_5}\mathrm{S}_{11}
&{\beta_6}\mathrm{S}_{13}
&{\beta_7}\mathrm{S}_{17}
&{\beta_8}\mathrm{S}_{19}
&{\beta_9}\mathrm{S}_{23}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
2^{\beta_1}
&3^{\beta_2}
&5^{\beta_3}
&7^{\beta_4}
&11^{\beta_5}
&13^{\beta_6}
&17^{\beta_7}
&19^{\beta_8}
&23^{\beta_9}
&\cdots
\\
\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
&\uparrow
\\
p_1{=}2
&p_2{=}3
&p_3{=}5
&p_4{=}7
&p_5{=}11
&p_6{=}13
&p_7{=}17
&p_8{=}19
&p_9{=}23
&\cdots
\\
\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
&\downarrow
\\
2^{-\alpha_1}
&3^{-\alpha_2}
&5^{-\alpha_3}
&7^{-\alpha_4}
&11^{-\alpha_5}
&13^{-\alpha_6}
&17^{-\alpha_7}
&19^{-\alpha_8}
&23^{-\alpha_9}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\alpha_1}\mathrm{s}_{2}
&{\alpha_2}\mathrm{s}_{3}
&{\alpha_3}\mathrm{s}_{5}
&{\alpha_4}\mathrm{s}_{7}
&{\alpha_5}\mathrm{s}_{11}
&{\alpha_6}\mathrm{s}_{13}
&{\alpha_7}\mathrm{s}_{17}
&{\alpha_8}\mathrm{s}_{19}
&{\alpha_9}\mathrm{s}_{23}
&\cdots
\\
\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
&\updownarrow
\\
{\alpha_1}\mathrm{t}
&{\alpha_2}\mathrm{d}
&{\alpha_3}\mathrm{m}
&{\alpha_4}\mathrm{q}
&{\alpha_5}\mathrm{n}
&{\alpha_6}\mathrm{r}
&{\alpha_7}\mathrm{p}
&{\alpha_8}\mathrm{u}
&{\alpha_9}\mathrm{v}
&\cdots
\end{matrix}
\right\}
$")
,
,
, который требует, однако, отдельного для него сообщения.![$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&:
&:
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{2d\mathsf{{:}T\o}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2Tt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TDd}}}
&\scriptstyle\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3T2t}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TMm}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TDdt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TQq}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}4T3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{C\sharp{-}30}{\underset{0,5448}{\mathsf{{:}Rq}}}
&\scriptstyle\overset{C\sharp{-}14}{\underset{0,5500}{\mathsf{{:}DM3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{2c\mathsf{{:}Q2t}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}2Dm}}}
&\scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}Ndt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}TQ3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{1b\mathsf{{:}Md}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}TMdt}}}
&\scriptstyle\overset{B\natural{+}31}{\underset{0,5029}{\mathsf{{:}2TDq}}}
&\scriptstyle\overset{B\natural{-}61}{\underset{0,4767}{\mathsf{{:}R3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}3Tm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{1a\mathsf{{:}Dt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}TD2t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2Ddt}}}
&\scriptstyle\overset{A\natural{+}81}{\underset{0,4610}{\mathsf{{:}Nq}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2TD3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}Qm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{G\sharp{+}16}{\underset{0,4190}{\mathsf{{:}TMq}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{1g\mathsf{{:}2Td}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}3Tdt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{+}49}{\underset{0,4033}{\mathsf{{:}N3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{1f\mathsf{{:}M2t}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{+}33}{\underset{0,3771}{\mathsf{{:}2Dq}}}
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}TM3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}TDm}}}
&\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}Qdt}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{+}29}{\underset{0,3352}{1e\mathsf{{:}3Tq}}}
&\scriptstyle\overset{E\natural{+}2}{\underset{0,3300}{\mathsf{{:}2D3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{1d\mathsf{{:}\O\o}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Tt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Dd}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2T2t}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Mm}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TDdt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Qq}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}3T3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,2567}{1c\mathsf{{:}Q3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}Mdt}}}
&\scriptstyle\overset{B\natural{+}31}{\underset{0,2514}{\mathsf{{:}TDq}}}
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{b\mathsf{{:}2Tm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{a\mathsf{{:}D2t}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}TD3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{G\sharp{+}16}{\underset{0,2095}{\mathsf{{:}Mq}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{g\mathsf{{:}Td}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}2Tdt}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,1833}{\mathsf{{:}M3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{f\mathsf{{:}Dm}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{+}29}{\underset{0,1676}{e\mathsf{{:}2Tq}}}
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{d\mathsf{{:}\O t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}T2t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Ddt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}2T3t}}}
\\
:
&:
&:
&:
&:
&:
&:
&:
\end{matrix}\right.
\left.\begin{matrix}
:
&:
&:
&:
&.\cdot
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}T2D2d}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TMmt}}}
&\scriptstyle\overset{D\natural{-}82}{\underset{0,5600}{\mathsf{{:}DQn}}}
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TNn}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3TDd2t}}}
&..
\\
\scriptstyle\overset{C\sharp{-}1}{\underset{0,5541}{\mathsf{{:}P2d}}}
&\scriptstyle\overset{D\flat{+}9}{\underset{0,5573}{\mathsf{{:}Umt}}}
&\scriptstyle\overset{C\sharp{-}67}{\underset{0,5333}{\mathsf{{:}2TMn}}}
&\scriptstyle\overset{C\sharp{+}24}{\underset{0,5622}{\mathsf{{:}Vd2t}}}
&..
\\
\scriptstyle\overset{C\natural{-}6}{\underset{0,5215}{\mathsf{{:}4T2d}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}T2Dmt}}}
&\scriptstyle\overset{C\natural{-}56}{\underset{0,5067}{\mathsf{{:}Un}}}
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}DQd2t}}}
\scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}TNd2t}}}
&..
\\
\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}DM2d}}}
&\scriptstyle\overset{B\natural{+}17}{\underset{0,4987}{\mathsf{{:}Pmt}}}
&\scriptstyle\overset{B\natural{-}49}{\underset{0,4800}{\mathsf{{:}T2Du}}}
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}2TMd2t}}}
&..
\\
\scriptstyle\overset{B\flat{-}37}{\underset{0,4563}{\mathsf{{:}TQ2d}}}
&\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}4Tmt}}}
&\scriptstyle\overset{A\sharp{-}48}{\underset{0,4533}{\mathsf{{:}Pn}}}
&\scriptstyle\overset{B\flat{-}6}{\underset{0,4644}{\mathsf{{:}Ud2t}}}
&..
\\
\scriptstyle\overset{A\natural{-}65}{\underset{0,4237}{\mathsf{{:}R2d}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}DMmt}}}
&\scriptstyle\overset{A\natural{-}53}{\underset{0,4267}{\mathsf{{:}4Tn}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}T2Dd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}TQmt}}}
&\scriptstyle\overset{G\sharp{-}65}{\underset{0,4000}{\mathsf{{:}DMn}}}
&\scriptstyle\overset{G\sharp{+}1}{\underset{0,4156}{\mathsf{{:}Pd2t}}}
&..
\\
\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}2TD2d}}}
&\scriptstyle\overset{G\natural{-}48}{\underset{0,3813}{\mathsf{{:}Rmt}}}
&\scriptstyle\overset{G\natural{-}84}{\underset{0,3733}{\mathsf{{:}TQn}}}
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}4Td2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}113}{\underset{0,3467}{\mathsf{{:}Rn}}}
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}DMd2t}}}
&..
\\
\scriptstyle\overset{F\natural{+}45}{\underset{0,3585}{\mathsf{{:}N2d}}}
&\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}2TDmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}TQd2t}}}
&..
\\
\scriptstyle\overset{E\natural{-}20}{\underset{0,3259}{\mathsf{{:}TM2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{-}51}{\underset{0,3200}{\mathsf{{:}2TDn}}}
&\scriptstyle\overset{E\natural{-}63}{\underset{0,3178}{\mathsf{{:}Rd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{E\flat{+}63}{\underset{0,3227}{\mathsf{{:}Nmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2D2d}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TMmt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Nn}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2TDd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{C\sharp{-}67}{\underset{0,2667}{\mathsf{{:}TMn}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{C\natural{-}6}{\underset{0,2607}{\mathsf{{:}3T2d}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,2640}{\mathsf{{:}2Dmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{+}47}{\underset{0,2689}{\mathsf{{:}Nd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}49}{\underset{0,2400}{\mathsf{{:}2Dn}}}
&\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}TMd2t}}}
&..
\\
\scriptstyle\overset{B\flat{-}37}{\underset{0,2281}{\mathsf{{:}Q2d}}}
&\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{\mathsf{{:}3Tmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{-}53}{\underset{0,2133}{\mathsf{{:}3Tn}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}2Dd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,2053}{\mathsf{{:}Qmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}TD2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}84}{\underset{0,1867}{\mathsf{{:}Qn}}}
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}3Td2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{\mathsf{{:}TDmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{-}35}{\underset{0,1711}{\mathsf{{:}Qd2t}}}
&..
\\
\scriptstyle\overset{E\natural{-}20}{\underset{0,1630}{\mathsf{{:}M2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{-}51}{\underset{0,1600}{\mathsf{{:}TDn}}}
&\color[rgb]{.6,.6,.6}\square
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Mmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}TDd2t}}}
&..
\\
:
&:
&:
&:
&\cdot.
\end{matrix}\right\}
$](https://dxdy-03.korotkov.co.uk/f/e/5/6/e565f4f03c96ce1f2139a3ce39c7055b82.png "$
\left\{\begin{matrix}
:
&:
&:
&:
&:
&:
&:
&:
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{2d\mathsf{{:}T\o}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2Tt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TDd}}}
&\scriptstyle\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3T2t}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TMm}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TDdt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TQq}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}4T3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{C\sharp{-}30}{\underset{0,5448}{\mathsf{{:}Rq}}}
&\scriptstyle\overset{C\sharp{-}14}{\underset{0,5500}{\mathsf{{:}DM3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{2c\mathsf{{:}Q2t}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}2Dm}}}
&\scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}Ndt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}TQ3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{1b\mathsf{{:}Md}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}TMdt}}}
&\scriptstyle\overset{B\natural{+}31}{\underset{0,5029}{\mathsf{{:}2TDq}}}
&\scriptstyle\overset{B\natural{-}61}{\underset{0,4767}{\mathsf{{:}R3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}3Tm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{1a\mathsf{{:}Dt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}TD2t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2Ddt}}}
&\scriptstyle\overset{A\natural{+}81}{\underset{0,4610}{\mathsf{{:}Nq}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2TD3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}Qm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{G\sharp{+}16}{\underset{0,4190}{\mathsf{{:}TMq}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{1g\mathsf{{:}2Td}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}3Tdt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{+}49}{\underset{0,4033}{\mathsf{{:}N3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{1f\mathsf{{:}M2t}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{+}33}{\underset{0,3771}{\mathsf{{:}2Dq}}}
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}TM3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}TDm}}}
&\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}Qdt}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{+}29}{\underset{0,3352}{1e\mathsf{{:}3Tq}}}
&\scriptstyle\overset{E\natural{+}2}{\underset{0,3300}{\mathsf{{:}2D3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{1d\mathsf{{:}\O\o}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Tt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Dd}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2T2t}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Mm}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TDdt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Qq}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}3T3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{-}33}{\underset{0,2567}{1c\mathsf{{:}Q3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}Mdt}}}
&\scriptstyle\overset{B\natural{+}31}{\underset{0,2514}{\mathsf{{:}TDq}}}
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{b\mathsf{{:}2Tm}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{a\mathsf{{:}D2t}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}TD3t}}}
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{G\sharp{+}16}{\underset{0,2095}{\mathsf{{:}Mq}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{g\mathsf{{:}Td}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}2Tdt}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,1833}{\mathsf{{:}M3t}}}
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{f\mathsf{{:}Dm}}}
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{+}29}{\underset{0,1676}{e\mathsf{{:}2Tq}}}
&\color[rgb]{.6,.6,.6}\square
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{d\mathsf{{:}\O t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}T2t}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Ddt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}2T3t}}}
\\
:
&:
&:
&:
&:
&:
&:
&:
\end{matrix}\right.
\left.\begin{matrix}
:
&:
&:
&:
&.\cdot
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}T2D2d}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TMmt}}}
&\scriptstyle\overset{D\natural{-}82}{\underset{0,5600}{\mathsf{{:}DQn}}}
\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TNn}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3TDd2t}}}
&..
\\
\scriptstyle\overset{C\sharp{-}1}{\underset{0,5541}{\mathsf{{:}P2d}}}
&\scriptstyle\overset{D\flat{+}9}{\underset{0,5573}{\mathsf{{:}Umt}}}
&\scriptstyle\overset{C\sharp{-}67}{\underset{0,5333}{\mathsf{{:}2TMn}}}
&\scriptstyle\overset{C\sharp{+}24}{\underset{0,5622}{\mathsf{{:}Vd2t}}}
&..
\\
\scriptstyle\overset{C\natural{-}6}{\underset{0,5215}{\mathsf{{:}4T2d}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}T2Dmt}}}
&\scriptstyle\overset{C\natural{-}56}{\underset{0,5067}{\mathsf{{:}Un}}}
&\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}DQd2t}}}
\scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}TNd2t}}}
&..
\\
\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}DM2d}}}
&\scriptstyle\overset{B\natural{+}17}{\underset{0,4987}{\mathsf{{:}Pmt}}}
&\scriptstyle\overset{B\natural{-}49}{\underset{0,4800}{\mathsf{{:}T2Du}}}
&\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}2TMd2t}}}
&..
\\
\scriptstyle\overset{B\flat{-}37}{\underset{0,4563}{\mathsf{{:}TQ2d}}}
&\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}4Tmt}}}
&\scriptstyle\overset{A\sharp{-}48}{\underset{0,4533}{\mathsf{{:}Pn}}}
&\scriptstyle\overset{B\flat{-}6}{\underset{0,4644}{\mathsf{{:}Ud2t}}}
&..
\\
\scriptstyle\overset{A\natural{-}65}{\underset{0,4237}{\mathsf{{:}R2d}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}DMmt}}}
&\scriptstyle\overset{A\natural{-}53}{\underset{0,4267}{\mathsf{{:}4Tn}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}T2Dd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}TQmt}}}
&\scriptstyle\overset{G\sharp{-}65}{\underset{0,4000}{\mathsf{{:}DMn}}}
&\scriptstyle\overset{G\sharp{+}1}{\underset{0,4156}{\mathsf{{:}Pd2t}}}
&..
\\
\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}2TD2d}}}
&\scriptstyle\overset{G\natural{-}48}{\underset{0,3813}{\mathsf{{:}Rmt}}}
&\scriptstyle\overset{G\natural{-}84}{\underset{0,3733}{\mathsf{{:}TQn}}}
&\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}4Td2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{F\sharp{-}113}{\underset{0,3467}{\mathsf{{:}Rn}}}
&\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}DMd2t}}}
&..
\\
\scriptstyle\overset{F\natural{+}45}{\underset{0,3585}{\mathsf{{:}N2d}}}
&\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}2TDmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}TQd2t}}}
&..
\\
\scriptstyle\overset{E\natural{-}20}{\underset{0,3259}{\mathsf{{:}TM2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{-}51}{\underset{0,3200}{\mathsf{{:}2TDn}}}
&\scriptstyle\overset{E\natural{-}63}{\underset{0,3178}{\mathsf{{:}Rd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{E\flat{+}63}{\underset{0,3227}{\mathsf{{:}Nmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2D2d}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TMmt}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Nn}}}
&\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2TDd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{C\sharp{-}67}{\underset{0,2667}{\mathsf{{:}TMn}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{C\natural{-}6}{\underset{0,2607}{\mathsf{{:}3T2d}}}
&\scriptstyle\overset{C\natural{+}16}{\underset{0,2640}{\mathsf{{:}2Dmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{C\natural{+}47}{\underset{0,2689}{\mathsf{{:}Nd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{B\natural{-}49}{\underset{0,2400}{\mathsf{{:}2Dn}}}
&\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}TMd2t}}}
&..
\\
\scriptstyle\overset{B\flat{-}37}{\underset{0,2281}{\mathsf{{:}Q2d}}}
&\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{\mathsf{{:}3Tmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{A\natural{-}53}{\underset{0,2133}{\mathsf{{:}3Tn}}}
&\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}2Dd2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\scriptstyle\overset{A\flat{-}19}{\underset{0,2053}{\mathsf{{:}Qmt}}}
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}TD2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{G\natural{-}84}{\underset{0,1867}{\mathsf{{:}Qn}}}
&\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}3Td2t}}}
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{\mathsf{{:}TDmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{F\natural{-}35}{\underset{0,1711}{\mathsf{{:}Qd2t}}}
&..
\\
\scriptstyle\overset{E\natural{-}20}{\underset{0,1630}{\mathsf{{:}M2d}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{E\natural{-}51}{\underset{0,1600}{\mathsf{{:}TDn}}}
&\color[rgb]{.6,.6,.6}\square
&..
\\
\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare
&..
\\
\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Mmt}}}
&\color[rgb]{.6,.6,.6}\square
&\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}TDd2t}}}
&..
\\
:
&:
&:
&:
&\cdot.
\end{matrix}\right\}
$")