А может, тогда не придумывать отсебятину, и называть собственное время собственным? Терминология с чем-то "истинным" в ОТО не распространена.
Я не придумываю отсебятину,я просто привык использовать понятия Логунова.

-координатные величины.

,

-физические (время и расстояния по покоящемся в данной СО приборам,находящимся в рассматриваемой точке).


Для которых(в данной точке) метрика:

Собственное же время для покоящихся часов:

(отвечает 2 событиям на часам,то есть для случая

)
Я имел ввиду просто,что в ЛЛ-2 упоминается только собственное время и физическое расстояние,физического времени для общего случая(то есть учетом неодновременности

)нет.Вот и все,я больше ничего не хотел сказать.
Я эти понятия и использую.
Я вам уже задавал вопрос. Придётся спросить в лоб: вы понятие сигнатуры знаете? Что оно означает? Что такое времениподобный интервал, пространственноподобный, светоподобный, изотропный?
Честно,не особо...
Времениподобный и пространтсвенноподобный,светоподобный - да.
А изотропный - это разве не то же самое,что светоподобный(нулевой)?
Такой операции ни в ОТО, ни в математике нигде нет. Так что, объясняйте, что она значит.
Ну,как я понимаю,значит переход к:


И построение выражения метрики,при котором,соответственно все поменяется местами.
(

становится то,где раньше было
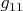
для

)
Время-то выделяется,среди остальных координат,поэтому и замена - не просто смена обозначений.
Наверное.



