Ещё способ. Берем в начале координат базис

и переносим в каждую точку области. Так как параллельный перенос сохраняет скалярное произведение, то метрический тензор будет постоянным:

Чтобы это было правильно, надо доказать, что полученный базис будет координатным, или голономным (а то так можно независимо от метрики взять в каждой точке ортонормированный базис и сказать, что у нас метрический тензор постоянный.

)
Итак, если векторное поле

получено таким переносом

и результат не зависит от способа переноса, то

для любого вектора

(что показал
Oleg Zubelevich). Следовательно, в нашем случае

. Тогда векторные поля

коммутируют:
![$[e_i, e_k]=\nabla_{e_i}e_k-\nabla_{e_k}e_i=0$ $[e_i, e_k]=\nabla_{e_i}e_k-\nabla_{e_k}e_i=0$](https://dxdy-01.korotkov.co.uk/f/c/5/c/c5c8957f54ea125f908522f64dce53e282.png)
Это и означает, что существуют такие функции

, что

.
Можно и так: независимость результата переноса любого вектора от пути означает и независимость переноса произвольного ковектора (1-формы)

от пути, что даёт

Но это означает, что

,
то есть
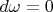
. Следовательно, по крайней мере в пределах данной карты

.
Применяя этот результат к базисным ковекторам, получим

.