drug39Спасибо!
amonТут не в аналитичность играем. Я понимаю, это ядро

вроде бы как производная
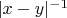
. Но ведь
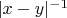
это тоже не обобщенная функция! Именно в этом вся специфика 1-мерного случая. Поэтому приходится вводить регуляризацию, и в вариационной задаче ответ будет

с

и потому мы заменяем ф-л на

.
Но тут дело ещё забавней из-за именно слабой, логарифмической расходимости. Поэтому

–окрестность исходной точки

вкладывает в энергию только

при любом

и потому основной вклад приходится на участок между

и

и потому форма сжимающегося тела не влияет на
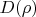
и ответ. А при потенциале

с

мы бы имели

с

но там бы

и там бы

бы зависело от формы. Например, если бы все сечения были бы подобны, то

где

- толщина сечения в

(до сжатия) и там бы

давало минимум.