Взяли:
Некорректно поставлено условие. Для перехода от покоящейся ИСО к движущейся ИСО', нужно применить «прямые» формулы ПЛ:
В данном случае как раз удобнее "обратные".
Применили:
Я Вас однажды спрашивал, что за эллипсы Вы рисуете и что видят неподвижные наблюдатели, находящиеся в точках этого эллипса. Увидят ли они одновременно проходящий в этом месте фронт светового сигнала? Вы так и не пожелали ответить.
Находим:
С.Мальцев явно продолжает придуриваться и делает не то, о чём его просят: вместо подстановки преобразований Лоренца в уравнение распространения света рисует тьму картинок. А формулы внезапно появляются в готовом виде. Поэтому свою задачу я решу сам.
Есть такое дело – туплю помаленьку. Это вот эти формулы от меня ув. Someone требовал?
Нет, не эти. Я вижу, Вы продолжаете придуриваться.
Чудес-то не бывает. И, если в одной из ИСО свет распространяется изотропно, то, с точки зрения здравого смысла, во всех прочих ИСО распространение света должно быть анизотропным, что наглядно и демонстрируют преобразования Лоренца.
Давайте Вы проделаете простое математическое упражнение. Возьмём уравнение фронта световой волны от точечной вспышки в той ИСО (будем называть её неподвижной), где свет распространяется изотропно:

. Сделаем преобразования Лоренца, чтобы перейти в движущуюся ИСО:

,

,

,

. И найдём уравнение фронта той же волны в движущейся ИСО. И увидим, следует ли из преобразований Лоренца, что свет в движущейся ИСО распространяется анизотропно.
Мне для решения этой задачи нужно написать две формулы, причём, вторая из них – это уравнение распространения света в движущейся системе. Если сделать преобразования подробнее, получится немного больше, но если не извращаться, дотянуть до Вашего объёма не удастся.
Вычисления я сделаю
очень подробно и с объяснениями, чтобы получилось "посолиднее".
Подставляя в уравнение

выражения для

из преобразований Лоренца, получим

Раскрываем скобки:

Члены

в левой и правой части сокращаются. Член

переносим в правую часть, член

– в левую. Получается

Далее в числителях дробей выносим множители за скобку и сокращаем дроби:


Таким образом, уравнение распространения света в движущейся инерциальной системе отсчёта имеет точно такой же вид, как и в неподвижной.
Поскольку

и

– время, измеряемое стандартными часами, неподвижными в соответствующих системах отсчёта, а

и

– координаты, измеряемые стандартными линейками, неподвижными в соответствующих системах отсчёта, приходится сделать вывод, прямо противоположный выводу
С.Мальцева: преобразования Лоренца "демонстрируют", что свет в движущейся инерциальной системе отсчёта распространяется так же изотропно, как и в неподвижной.
Таким образом, в любом случае, распространение света в движущейся ИСО' – анизотропно.
Я хочу подчеркнуть, что речь идёт именно об изотропности
распространения света. Не о его яркости или частоте, а именно о скорости и только о скорости. Яркость и частота определяются в момент излучения, и если источник, изотропный в одной ИСО, становится анизотропным в другой (из-за аберрации и эффекта Доплера), то это уже другой вопрос, не имеющий отношения к собственно распространению. Задача и формулировалась таким образом, что в ней речь шла
только о скорости распространения света в разных направлениях.
Также просто разобраться и с аберрацией. Рассматриваем те же системы отсчёта, что и в предыдущем случае. Пусть световой сигнал распространяется в неподвижной системе отсчёта в плоскости

под углом

к оси

и в момент

проходит через начало координат, а в движущейся системе угол между направлением распространения сигнала и осью

обозначим
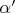
.
Уравнения движения светового сигнала в неподвижной системе отсчёта имеют вид

,

,

, а в движущейся –

,

,

.
Подставляя в уравнение

выражения

,

, а затем

, получим




Аналогично можно получить формулы

