Как учит уважаемый mihaild, патологические случаи, когда графа мало и надо изучать метрику, имеют меру ноль, и большую часть того что пригодно в народном хозяйстве можно охватить графами.
Сильно сомневаюсь, что он учит такому.

Ибо кривошипно-шатунные механизмы широко применяются в народном хозяйстве, в каждом ДВС и не только

Да, я расширил тут тему стартовую тему топика, где скользящие связи не применялись.
В двумерии (палки на столе) взаимное положение

точек определяется

-мя независимыми уравнениями. На физическом уровне строгости это получается из того, что каждая вершина имеет две степени свободы, и из полного числа таких степеней надо вычесть три степени свободы (два сдвига и поворот) всех точек как целого.
Если посчитать, как "палки движутся", а соединения ограничивают, то через формулу подвижности в двумерии, условие на жёсткость:
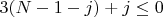
, где

- количество ребер,

- количество соединений, "шарниров".
Можно перейти от количества шарниров к количеству вершин и их степеням:
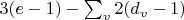
.
тут

- количество ребер,
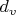
- степень вершины

, суммирование по всем вершинам.
-- 05.02.2026, 11:00 --Можно ли свести одно к другому - не знаю
 -- 05.02.2026, 11:10 --
-- 05.02.2026, 11:10 --В 3D в условиях стартового поста тоже можно сделать формулу подвижности.
1. Количество степеней свободы несвязанных ребер:

2. Движение системы, как единого целого не интересует:
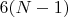
3. Вращательное движение ребер вокруг оси ребра не интересует, итого степеней свободы:
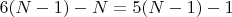
4. Каждое соединение сохраняет 3 вращательные степени свободы, и запрещает три поступательных.
5. Итого, формула мобильности и условие жёсткости:
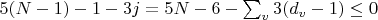
Интересно, что по этой формуле мобильность треугольника ноль, а не отрицательное число. И это хорошо.
Понятно, что формулы мобильности не учитывают вырождение системы связей, в частности появление подвижности, когда формула подвижности запрещает.
Но вот таких случаев количество меры ноль. Но они-то как раз могут быть интересны.