Жесткость сооружений из палочек.

[mihaild]

EUgeneUS в сообщении #1717060 писал(а):

шарнир - осталась одна степень свободы

Я не знаю таких страшных слов, как "шарнир" (и мне кажется естественным задавать вложение графа координатами вершин, а не ребер). Но вроде бы для нашей задачи (с графом) вершина, в которой соединено $k$ ребер, уменьшает число степеней свободы на $2(k-1)$ (одно ребро распологается как угодно, а у всех остальных из трех степеней остается одна - угол с выбранным), так?
Тогда число степеней свободы всей системы $3e - \sum_v 2(d_v - 1)$, где $d_v$ - степень вершины $v$.
В примере выше $8$ ребер, $4$ вершины степени $3$, $2$ вершины степени $2$. Итого число степеней свободы всей системы $24 - 4 \cdot 2 \cdot 2 - 2 \cdot 2 \cdot 1 = 4$. Многовато будет.

[EUgeneUS]

mihaild в сообщении #1717107 писал(а):

Но вроде бы для нашей задачи (с графом) вершина,

Граф на плоскости или в пространстве?

mihaild в сообщении #1717107 писал(а):

вершина, в которой соединено $k$ ребер, уменьшает число степеней свободы на $2(k-1)$ (одно ребро распологается как угодно, а у всех остальных из трех степеней остается одна - угол с выбранным), так?

На плоскости - так, но с уточнением ниже.

mihaild в сообщении #1717107 писал(а):

В примере выше $8$ ребер, $4$ вершины степени $3$, $2$ вершины степени $2$.

С третьей попытки нашел пример, о котором речь.

mihaild в сообщении #1717107 писал(а):

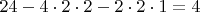
Итого число степеней свободы всей системы $24 - 4 \cdot 2 \cdot 2 - 2 \cdot 2 \cdot 1 = 4$. Многовато будет.

В самый раз.
На плоскости имеем в данном примере при данном расчете - 3 степени свободы, как у твердого тела (на плоскости - одна вращательная и две поступательных), и одна степень свободы - движение четырехзвенного механизма, который включает две вершины степени $2$.
В примере, как на рисунке, четырехзвенный механизм двигаться не будет по причине, указанной выше.

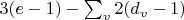
Чтобы не учитывать степени свободы "как у твердого тела", одно ребро считают фиксированным, жёстко закрепленным. Тогда формулу для плоского механизма в Вашей нотации, нужно переписать так: $3(e-1) - \sum_v 2(d_v - 1)$. И получим $1$ степень свободы.

-- 03.02.2026, 15:29 --

mihaild в сообщении #1717107 писал(а):

Я не знаю таких страшных слов, как "шарнир"

Это печально.
Ибо на плоскости-то всё равно. Там один вид шарниров бывает.
А вот в 3D - три разных вида, которые оставляют, одну, две или три вращательные степени свободы.
И когда говорим о графе (механизме) в 3D, указание типа соединения ребёр становится обязательным.

А ещё бывают скользящие сочленения.

[amon]

EUgeneUS в сообщении #1717060 писал(а):

Вот и свели к треугольникам.

А это - тривиальный пример. Попробуйте "свести к треугольникам" конструкцию уважаемого B@R5uk

$$\begin{tikzpicture} \draw(0,1)--(0.78,0.62)--(0.97,-0.22)--(0.43,-0.9)--(-0.43,-0.9)--(-0.97,-0.22)--(-0.78,0.62)--(0,1); \draw(0.43,-0.9)--(0,1)--(-0.43,-0.9); \draw(0.78,0.62)--(-0.97,-0.22); \draw(-0.78,0.62)--(0.97,-0.22); \end{tikzpicture}$$

(Она жесткая.) Или выпуклый шестиугольник с диагоналями, соединяющими противоположные вершины (тоже, вроде, жесткий).

[Sender]

Вообще, в википедии приводится ссылка на статью, в которой выводятся ограничения области применимости обсуждаемого критерия, подробно не разбирался, но вроде бы для графов связей с несколькими перекрывающимися циклами не всегда выполняется.

[Geen]

amon в сообщении #1717129 писал(а):

Попробуйте "свести к треугольникам"

Редуцируем треугольник в точку (двуугольник тоже)... пока не останется одна точка.

[amon]

На сколько я помню, выпуклый N-угольник определяется $2N-3$-мя независимыми элементами. Для невыпуклого это, вроде, не так.

[EUgeneUS]

Geen в сообщении #1717133 писал(а):

Редуцируем треугольник в точку (двуугольник тоже)... пока не останется одна точка.

Нельзя так.
Представим четырёхугольник и имеющий с ним общее ребро треугольник.
Четырёхугольник имеют одну степень свободы, треугольник - ноль.
Если "стянем" треугольник в точку, то четырёхугольник превратится в треугольник и степень свободы потеряется.

[mihaild]

EUgeneUS в сообщении #1717118 писал(а):

Граф на плоскости или в пространстве?

Вообще и те, и те рассматриваются. В моем последнем сообщении - только на плоскости.

EUgeneUS в сообщении #1717118 писал(а):

В примере, как на рисунке четырехзвенный механизм, двигаться не будет, по причине указанной выше

По какой причине?

EUgeneUS в сообщении #1717060 писал(а):

если в замкнутый цикл соединены более трех ребер, при этом суммарная длина всех ребер, кроме одного, равна длине (одного) оставшегося

Такого не происходит.

EUgeneUS в сообщении #1717118 писал(а):

$3(e-1) - \sum_v 2(d_v - 1)$

Теперь т.к. $\sum d_v = 2e$, получаем $3e - 3 - 4e + 2v = 2v - 3 - e$. Что совпадает с формулой из "The rigidity of graphs" (там говорится, что если это больше нуля, то граф нежесткий при всех регулярных вложениях).

Возникает вопрос - является ли равенство нулю числа степеней свободы критерием жесткости при регулярных вложениях. Вроде бы во всех примерах выше, и из статьи, его нарушение (жесткость при на наличи степеней свободы и гибкость при отсутствии) происходит только при нерегулярных.

[amon]

Пока вымучилось такое "необходимое условие жесткости": если внешний контур конструкции представляет собой выпуклый N-угольник, то вся конструкция должна содержать не менее чем $2N-3$ палок. Уже что-то. Обобщить бы на трехмерию, и можно статью в какой-нибудь строительный журнал писать;)

-- 03.02.2026, 19:12 --

Для выпуклого многогранника, вроде, получается минимальное число палок $3V-6,$ где $V$ - число вершин многогранника.

[EUgeneUS]

mihaild в сообщении #1717138 писал(а):

Такого не происходит.

именно такое и происходит.
Два треугольника образуют твердое тело.
И если у нас есть две точки на твердом теле, то совершенно без разницы (в контексте подвижности) какой формы твердое тело между ними: в виде отрезка прямой (ребра), или в виде какой-то загогулины.

mihaild в сообщении #1717138 писал(а):

Возникает вопрос - является ли равенство нулю числа степеней свободы критерием жесткости при регулярных вложениях. Вроде бы во всех примерах выше, и из статьи, его нарушение (жесткость при на наличи степеней свободы и гибкость при отсутствии) происходит только при нерегулярных.

Тут приношу извинения, не очень понимаю терминологию про регулярные вложения.

mihaild в сообщении #1717138 писал(а):

Вообще и те, и те рассматриваются.

при рассмотрении в 3D мало заявить, что соединения в вершинах подвижны. Нужно указать - как именно подвижны.
На плоскости, да, достаточно заявить, что соединения в вершинах подвижны (и неявно предполагать, что нет скользящих соединений, то есть вершины всегда остаются вершинами, а ребра не меняют длину).

[mihaild]

EUgeneUS в сообщении #1717163 писал(а):

про регулярные вложения

Я выше примерно писал, но на случай если понадобится, напишу нормально.
У нас есть граф $(V, E)$. Вложением графа в $\mathbb R^n$ называется инъективная функция $V \to \mathbb R^n$. Функция рёбер $f: \mathbb R^{nv} \to \mathbb R^e$ определяется $f(\vec v_1, \vec v_n)_i = \|v_{e_{i, 1}} - v_{e_{i, 2}}\|^2$, где $e_{i, 1}$ и $e_{i, 2}$ - вершины, инцидентные $i$-му ребру.
У функции ребёр в каждой точке есть дифференциал $df$. У дифференциала есть ранг, максимальный (по всем точкам) ранг обозначим $k$.
Вложение называется регулярным, если ранг $df$ в нём равен $k$. Почти все (в смысле меры Лебега) вложения регулярны.

EUgeneUS в сообщении #1717163 писал(а):

именно такое и происходит

Где там цикл, в котором длина одного ребра равна сумме длин всех остальных?

EUgeneUS в сообщении #1717163 писал(а):

Нужно указать - как именно подвижны

amon в сообщении #1716909 писал(а):

палки соединены концами и могут как угодно крутиться относительно друг друга в точке соединения

[amon]

То есть, среди правильных многогранников не жесткие только куб и додекаэдр.

[EUgeneUS]

mihaild в сообщении #1717167 писал(а):

Я выше примерно писал,

Спасибо! Я попытаюсь разобраться (для этого нужно некоторое время непрерывным куском ).

mihaild в сообщении #1717167 писал(а):

Где там цикл, в котором длина одного ребра равна сумме длин всех остальных?

Так нарисуйте его, это одно ребро
Стандартные разногласия между физиками и математиками.
Вы считаете, что раз ребра нет в заданном графе, то его и нет.
А я считаю, что если две точки заданы на твердом теле, то расстояние между ними - константа. И без разницы, есть между этими точками жесткая прямая палка, или там какая-то загогулина (из двух треугольников).

mihaild в сообщении #1717167 писал(а):

amon в сообщении #1716909

писал(а):
палки соединены концами и могут как угодно крутиться относительно друг друга в точке соединения

И все таки уточню, "как угодно" - это сколько вращательных степеней свободы? Две или три?
Например, если три (как угодно же), то у треугольника будет три степени свободы

-- 03.02.2026, 20:18 --

EUgeneUS в сообщении #1717172 писал(а):

Так нарисуйте его, это одно ребро

Грубо говоря. Если оказалось, что какой-то подграф - жесткий, то его можно заменить полным (под)графом с теми же вершинами.

[EUgeneUS]

mihaild
Пытаюсь разобраться.

(Оффтоп)

mihaild в сообщении #1717167 писал(а):

Функция рёбер $f: \mathbb R^{nv} \to \mathbb R^e$ определяется $f(\vec v_1, \vec v_n)_i = \|v_{e_{i, 1}} - v_{e_{i, 2}}\|^2$, где $e_{i, 1}$ и $e_{i, 2}$ - вершины, инцидентные $i$-му ребру.

Правильно ли я понимаю, по рабоче-крестьянски, что "функция ребер"
а) это функция размерности $e$, где $e$ - это количество ребер.
б) а для каждого ребра, считается квадрат меры (расстояния), как функции от положений концов ребра
?
Если да, то мне не понятны индексы при $v$ в правой части равенства, вот здесь: $$f(\vec v_1, \vec v_n)_i = ...$

mihaild в сообщении #1717167 писал(а):

У дифференциала есть ранг, максимальный (по всем точкам) ранг обозначим $k$.

Правильно ли я понимаю, что максимальный ранг дифференциала ищется по всем возможным размещениям вершин графа в $\mathbb{R}^n$ ?

[mihaild]

EUgeneUS в сообщении #1717231 писал(а):

Если да, то мне не понятны индексы при $v$ в правой части равенства, вот здесь: $$f(\vec v_1, \vec v_n)_i = ...$

В левой части я многоточие потерял. Индексы справа - это концы ребра как раз.
Т.е. если $i$-е ребро соединяет вершины $a$ и $b$, то $f(\vec v_1, \ldots, \vec v_n)_i = \|\vec v_a - \vec v_b\|^2$.

EUgeneUS в сообщении #1717231 писал(а):

Правильно ли я понимаю, что максимальный ранг дифференциала ищется по всем возможным размещениям вершин графа в $\mathbb{R}^n$ ?

Да.