Жесткость сооружений из палочек.

[mihaild]

ozheredov в сообщении #1716949 писал(а):

А как определяется не-жесткость?

Там два определения:
1. Вложение называется жестким, если любое другое достаточно близкое вложение, сохраняющее длины ребер графа, сохраняет все расстояния между вершинами.
2. Вложение называется гибким, если существует непрерывное движение вершин, сохраняющее длины ребер графа, но не все расстояния между вершинами (т.е. не являющееся движением всего $\mathbb R^n$).
И доказывается, что не-жесткость эквивалентна гибкости.

ozheredov в сообщении #1716949 писал(а):

А можно ли доказать, что все по разному вложенные в $R^n$ графы с одной и той же взвешенной матрицей смежности (вес = длина ребра) могут быть только либо одновременно жесткими, либо одновременно не-жесткими?

Из статьи ответ на этот вопрос не следует. И я сходу ничего не придумал.

[B@R5uk]

amon в сообщении #1716937 писал(а):

Контрпример. Согласно Вашей формуле устойчивость определяется только числом узлов и связей.

Нет, не только, я же написал, что связи могут быть зависимыми друг от друга:

B@R5uk в сообщении #1716913 писал(а):

Проблемы могут настать, когда некоторые связи являются выражаемыми через другие, зависимыми от других. Но чтобы это произошло надо обычно очень постараться.

В вашем контрпримере именно так и происходит. Составьте матрицу производных связей (как я описал здесь) и убедитесь в линейной зависимости её строк самостоятельно.

mihaild в сообщении #1716948 писал(а):

Если сделать нижние ребра немного длиннее, то их станет возможным двигать. Если же они натянуты за счет двух треугольников - то нет.

О! Это классный пример. Но чтобы "увидеть" его жёсткость, мне кажется, что линейного приближения будет недостаточно.

[mihaild]

ozheredov в сообщении #1716949 писал(а):

Или это вообще не так?

Сообразил, что есть очевидный контрпример.
Рассмотрим две треугольные пирамиды разной высоты, склеенные основаниями, и путь из двух ребер, соединяющий вершины. Мы можем пирамиды склеить так, что либо их вершины окажутся по разные стороны от общего основания, либо по одну. Длину пути между вершинами сделаем равной расстоянию между вершинами, если вершины по разные стороны от основания. Тогда, если пирамиды переклеить - так что вершины будут по одну сторону от основания - длина между их вершинами уменьшится, соединяющий их путь изогнется, и его станет возмножно крутить вокруг соединяющей вершины прямой.

[ozheredov]

mihaild
Thanks!

[amon]

Спасибо всем откликнувшимся, отдельное спасибо mihaild. Задачка оказалась гораздо сложнее чем мне казалось, и относительно простого "критерия жесткости", видимо нет.

[B@R5uk]

amon, мне кажется, что если к моему линейному критерию выше добавить проверку второго порядка, то всё станет однозначно ясно. Нужно убедиться, что матрица вторых производных длин рёбер после сужения на подпространство ядра матрицы первых производных, являющееся (в ядре) ортогональным дополнением подпространству движений тела как целого, становится положительно определённой формой (а не положительно полуопределённой или вообще неопределённой). Тогда, очевидно, нельзя будет указать такое движение точек (кроме движений тела как целого), которое бы не приводило к изменению длин рёбер. При этом, если при построении производных рассматривать не длины палочек, а квадраты длин, то больше второго порядка проверять будет и не надо. Просто потому что все производные после этого будут нулевыми (квадрат длины палочки равен сумме квадратов разностей координат концов — полином второго порядка, третья и старшие производные нулевые).

Я бы не сказал, что вычисление производных и составления всех этих матриц — это простое занятие. Лично для меня это концептуально просто, а все описанные выше этапы — хорошо известные из курса линейной алгебры вещи и технически легко реализуемы с использованием соответствующего пакета (в MATLAB'е, например). Но мой опыт приходит из попыток численного решения задачи Таммеса. Там тоже точки, рёбра, связи, зависимости и необходимость жёсткости фигуры. В любом случае, алгоритм нахождения ответа на ваш вопрос есть.

[Sender]

Если заменить часть палочек на гибкие тросики с сохранением требования жёсткости конструкции, мы получим напряжённо-связанные конструкции (tensegrity structures), они нередко выглядят довольно контринтуитивно.
https://en.wikipedia.org/wiki/Tensegrity

[EUgeneUS]

1.

Цитата:

Критерий Чебышева - Грюблера-Кутцбаха определяет число степеней свободы кинематической цепи , то есть связи жестких тел посредством механических ограничений

2.

Цитата:

В машиностроении перегруженный механизм — это звеньевой механизм , имеющий больше степеней свободы , чем предсказывает формула подвижности .

[amon]

EUgeneUS, простой подсчет числа степеней свободы не помогает, важно еще как соединены ребра, что показывают мои картинки. Для каждого частного случая не очень сложно оценить жесткость просто решая систему
$(\mathbf{r}_i-\mathbf{r}_j)^2=l_i^2$
относительно косинусов углов. Начало координат удобно поместить в узел с максимальным числом выходящих из него ребер. Тогда движение сооружения как целого автоматически исключается. У меня была иллюзия, что ответ (единственность решения) зависит только от топологии графа и на этом можно придумать какой-нибудь относительно простой критерий. mihaild эту иллюзию развеял.

[EUgeneUS]

amon

Если критерий подвижности говорит, что система имеет степени свободы, то она будет обязательно иметь степени свободы, столько или больше.

Если критерий подвижности показывает ноль или меньше степеней свободы, то два варианта:
а) либо система неподвижна.
б) либо степени свободы есть. Но тогда это "overconstrained mechanism", а у них подвижность возникает только при определенных геометрических параметрах (углах, линейных размерах...). Это не описывается графом.

Есть ли какие-то методы определения является ли система "overconstrained mechanism" - или нет, не знаю.
С темой знаком весьма поверхностно, на основе обсуждения топика про Турбулу.

[mihaild]

EUgeneUS
Я правильно понимаю, что для случая графа число степеней свободы в критерии подвижности это просто $nv - (n - 1)e$? (каждая вершина имеет $n$ степеней свободы, каждое ребро ограничивает $n-1$ степень) И т.к. у нас есть $2n - 1$ степень движения как целого (сдвиг + поворот), то критерий говорит, что достаточное условие подвижности $nv - (n - 1) e > 2n - 1$?
Тогда вот выше пример с $n=2$, $v=6$, $e=8$.

[Sender]

mihaild, не совсем.
Для случая плоского движения получается мобильность, если я правильно понимаю, $M=3(N-1-j)+\sum\limits_{i=1}^jf_i=1$,
где $N$ - общее число движущихся тел плюс одно фиксированное тело.
$j$ - число сочленений,
$f_i=1$ - степени свободы сочленений.
Но что-то всё равно не ноль, да.

[mihaild]

Sender в сообщении #1717022 писал(а):

$M=3(N-1-j)+\sum\limits_{i=1}^jf_i=1$,
где $N$ - общее число движущихся тел плюс одно фиксированное тело.

Мне как-то очень подозрительно, что добавление ни с чем не связанной вершины добавляет 3 степени свободы, а не две.

[Sender]

mihaild в сообщении #1717024 писал(а):

Мне как-то очень подозрительно, что добавление ни с чем не связанной вершины добавляет 3 степени свободы, а не две.

Видимо, две поступательных и вращательную.

[EUgeneUS]

mihaild в сообщении #1717021 писал(а):

(каждая вершина имеет $n$ степеней свободы, каждое ребро ограничивает $n-1$ степень)

Я, конечно, понимаю, что у каждого графа есть дуальный. Но попытка представить вышеописанное привела к мигрени.

Мне удобнее считать так:
1. Ребро - это палка, количество степеней свободы у неё:

а) в плоском случае - 3 (две поступательных, одна вращательная).
б) в 3D
- либо 6 (три поступательных, три вращательных).
- либо 5 (три поступательных, две вращательных), если вращение вокруг оси не учитываем. Этот вариант ниже не рассматривается

2. А вот вершины - это подвижные соединения. Которые могут ограничивать разное количество степеней свободы, в зависимости от конструкции:

а) шарнир - осталась одна степень свободы,
б) карданный шарнир - осталось две степени свободы,
в) обычный шарнир плюс вращающаяся муфта, плюс вращение в муфте вокруг оси ребра - осталось три степени свободы,
г) как пункт в), но скользящая муфта - осталось четыре степени свободы.
и т.д.

-- 03.02.2026, 11:07 --

Формулу подвижности нужно применять аккуратно и вдумчиво.
В частности, вот тут я поспешил:

EUgeneUS в сообщении #1717018 писал(а):

Если критерий подвижности говорит, что система имеет степени свободы, то она будет обязательно иметь степени свободы, столько или больше.

Есть класс (как минимум один) соединений, когда формула подвижности показывает подвижность, но система жесткая:
если в замкнутый цикл соединены более трех ребер, при этом суммарная длина всех ребер, кроме одного, равна длине (одного) оставшегося.

Не знаю, есть ли другие подобные классы.

Далее рассмотрим на примере треугольников.

-- 03.02.2026, 11:20 --

1. Треугольник в 3D с обычными шарнирами в вершинах.

$$M = 6(N - 1 - j) +\sum\limits_{i=1}^{j}f_i = -6 + 3 = -3$$

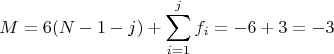
Система жесткая.

2. Треугольник в 3D с карданными шарнирами в вершинах.

$$M = 6(N - 1 - j) +\sum\limits_{i=1}^{j}f_i = -6 + 6 = 0$$

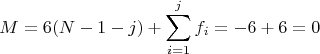
Система жесткая.

3. Треугольник в 3D с обычными шарнирами в вершинах, плюс ещё одна палка на карданном шарнире в любой точке треугольника.

$$M = 6(N - 1 - j) +\sum\limits_{i=1}^{j}f_i = -6 + (3+2) = -1$$

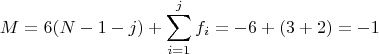
Система, вроде бы жесткая.
Ан-нет. У неё две степени свободы в карданном подвесе четвертого ребра.
Потому что $-3$ от "избыточной" жёсткости треугольника убило при подсчете эти две степени свободы.

Поэтому, хорошо бы при анализе выделять треугольники (с нескользящими шарнирами в вершинах) и считать их твердыми телами.

4. Треугольник: два шарнира в двух вершинах, в третьей вершине шарнир на скользящей муфте, оси всех шарниров перпендикулярны плоскости треугольника:
а) в 3D

$$M = 6(N - 1 - j) +\sum\limits_{i=1}^{j}f_i = -6 + (3+1) = -2$$

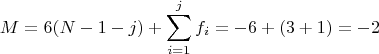
Система вроде бы жесткая.
Но, очевидно, система подвижная с одной степенью свободы.
"оверконстрейнтед механизм".

Даже понятно, почему так получается - "специальная геометрия": оси всех шарниров перпендикулярны плоскости треугольника.
Без этого условия система действительно будет жесткой.

б) в 2D, так как случай плоский

$$M = 3(N - 1 - j) +\sum\limits_{i=1}^{j}f_i = -3 + (3+1) = 1$$

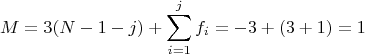
Верный ответ.

-- 03.02.2026, 11:44 --

dsge в сообщении #1716917 писал(а):

а равнобедренная (и не только) трапеция уже жесткая.

Чёй-та?

-- 03.02.2026, 11:48 --

amon в сообщении #1716921 писал(а):

$$\begin{tikzpicture} \draw (0,0) rectangle (1,1); \draw (0,0) -- (-1,0.5) --(0,1); \draw (0,0) -- (0.5,-1) -- (1,0); \draw (-1,0.5)--(0.5,-1); \end{tikzpicture}$$

Треугольники - жесткие.
Так как система плоская - соединение треугольников по ребру - жесткое.
В результате имеем твердое тело из трех имеющихся на рисунке треугольников.
Вершины диагонали квадрата принадлежат твердому телу, а значит между ними может быть расположено жесткое ребро.
Вот и свели к треугольникам.