Биекция мн. чисел вида (m/2^n), m,n-Z во мн.Q возрастающая?

[cxzbsdhwert]

mihaild, может всё было куда прозаичнее?

1. Всё-таки аргументом функции, если представлять рациональные числа парой целых, должна быть пара целых $(m,n)$ где $m$ и $n$ это числитель и знаменатель а не числитель и степень двойки, которая составляет знаменатель.
2. Мн-во чисел вида $\frac{m}{2^n}$ обозначим за $X$.
3. Пускай нужная функция $f:\mathbb Q \rightarrow X$ это просто $f:(m,n)\rightarrow(m,2^n)$, а обратная ей $f^{-1}:(m,n)\rightarrow(m,\log_2n)$.
4. Ограничим область определения для функции и обратной так: $\text{НОД}(m,n)=1$, $\text{НОД}(m,2^n)=1$, $n\geq 0$ — выше доказывалось что с такими ограничениями это всё те же множества $X$ и $\mathbb Q$.
5. Покажем что функция возрастающая: при приросте дроби-аргумента $\frac{m}{n}$ на единицу, её вид будет $\frac{m}{n}+1=\frac{m+n}{n}$. Тогда нам нужно показать что $\frac{m+n}{2^n}>\frac{m}{2^n}$. При нашем дополнительном условии $n\geq 0$ (ну по крайней мере строго больше) — верность неравенства очевидна.
6. Докажем что функция инъективна. Покажем что $\frac{m}{2^n}=\frac{p}{2^q}$ $\iff m=p \text{И} n=q$:
$m=2^{n-q}p$. По дополнительному условию $\text{НОД}(m,2^n)=1$, но это это значит что не только энная степень но и сама двойка не является делителем $m$, а значит $m$ нечётно.
Но тогда $m=2^{n-q}p$ верно только если $n=q$ (кроме $m=p=0$, разумеется). А если $n=q$, то $m=p$, а значит функция инъективна.

[mihaild]

cxzbsdhwert в сообщении #1715760 писал(а):

Пускай нужная функция $f:\mathbb Q \rightarrow X$ это просто $f:(m,n)\rightarrow(m,2^n)$,

Если я правильно понял, что вы хотите, то это пишется так: если $\frac{m}{n}$ несократима, то $f\left(\frac{m}{n}\right) = \frac{m}{2^n}$.

cxzbsdhwert в сообщении #1715760 писал(а):

$\text{НОД}(m,n)=1$, $\text{НОД}(m,2^n)=1$

Нехорошо так писать. Обозначьте аргументы $f$ и $f^{-1}$ разными буквами.

cxzbsdhwert в сообщении #1715760 писал(а):

Покажем что функция возрастающая: при приросте дроби-аргумента $\frac{m}{n}$ на единицу, её вид будет $\frac{m}{n}+1=\frac{m+n}{n}$

Этого недостаточно для возрастания.

[ИСН]

У вашей функции масса проблем. Вот одна: куда переходит из $\mathbb Q$ число $4\over5$? В $\frac4{32}=\frac18$. А обратная функция его перекинет куда? В $1\over3$? Упс...

[Someone]

cxzbsdhwert, я сразу Вам написал, как надо действовать: https://dxdy.ru/post1695441.html#p1695441. Это третье сообщение в вашей теме.

Вы уже 4 страницы канителитесь с дробями $\frac mn$ и $\frac m{2^n}$ (в частности, это моё сообщение — уже шестьдесят четвёртое сообщение данной темы). Если Вы не бросите заниматься фигнёй и не возьмётесь за ум, то потратите ещё 100 страниц с нулевым результатом.

Someone в сообщении #1695441 писал(а):

Щелью в линейно упорядоченном множестве называется пара элементов, между которыми нет других элементов.

Виноват, это называется не щелью, а скачком. Щель — это такое сечение $(A,B)$, что в $A$ нет наибольшего элемента, а $B$ нет наименьшего элемента. Надеюсь, определение сечения в линейно упорядоченном множестве Вы знаете.

[cxzbsdhwert]

mihaild в сообщении #1715761 писал(а):

Этого недостаточно для возрастания.

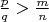
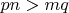
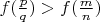
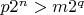
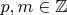
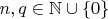
Производных ещё не было. Функция всё равно не подходит, дальше написано, но формально я бы тогда выкрутился так: пусть для произвольного аргумента $\frac{m}{n}$, аргумент $\frac{p}{q}>\frac{m}{n}$, а значит $pn>mq$. Покажем что $f(\frac{p}{q})>f(\frac{m}{n})$: получим $p 2^n>m 2^q$. Ну вроде при $p,m\in\mathbb Z$ и $n,q\in \mathbb N \cup \{0\}$ это так (по крайней мере $\geq$).

mihaild в сообщении #1715761 писал(а):

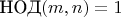
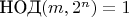
$\text{НОД}(m,n)=1$, $\text{НОД}(m,2^n)=1$ Нехорошо так писать. Обозначьте аргументы $f$ и $f^{-1}$ разными буквами.

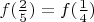
Так оба этих ограничения одновременны на биекцию в обе стороны. Иначе например $f(\frac{2}{5})=f(\frac{1}{4})$, т.к. $\frac{2}{2^5}=\frac{1}{2^4}$.
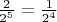
Но тогда получается что функция не все рациональные ставит в соответствие элементам $X$.

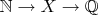
И тут я подумал: а не розыгрыш ли это? Доказать существование возрастающей биекции из $X$ в $\mathbb Q$. Но $X$ же как и $\mathbb Q$ счётно. А если $X$ счётно то существует биекция $\mathbb N$ в $X$. А если существует возрастающая биекция из $X$ в $\mathbb Q$, то можно взять композицию $\mathbb N \rightarrow X \rightarrow \mathbb Q$, композиция биекций - биекция. Но возрастающей биекции с $\mathbb N$ на $\mathbb Q$, насколько я понимаю, быть не может.
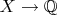
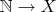
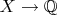
Или что? Биекция $X\rightarrow \mathbb Q$ возрастающая при определённом порядке самого $X$, а порядок $\mathbb N \rightarrow X$ будет отличен? Может тогда можно адаптировать возрастание $X\rightarrow \mathbb Q$ под порядок, который возникает при $\mathbb N \rightarrow X$?

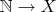
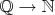
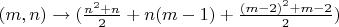
Как вообще биекцию $\mathbb Q \rightarrow \mathbb N$ задать? Формула выведенная по "диагональному методу" была на лекции, я её и сам выводил это $(m,n)\rightarrow (\frac{n^2+n}{2}+n(m-1)+\frac{(m-2)^2+m-2}{2})$, но формально это была формула биекции $\mathbb N$ на декартово произведение произвольных счётных множеств. Лектор также уточнил, что представляя рациональные числа (ну Он не совсем про них говорил) таблицей нужно будет "выбрасывать" сокращаемые дроби, и либо пропускать такие пары $(m,n)$ либо заменять их на несокращаемые.
Но как это фактически учесть формульно? Может это не реально?

-- 23.01.2026, 20:10 --

ИСН
Да, я это уже предвосхитил от части. Проблема явно с чётным числителем. Я как уже написано выше это ограничил, но тем не менее та же $\frac{4}{5}$ это несокращаемая дробь, которая соответствует уникальному рациональному числу, и если мы её выкинули, то это просто будет не функция (с одной стороны) или не сюръекция (с точки зрения обратной). Возможно нужно придумать отдельное правило сопоставления для чётных числителей.

-- 23.01.2026, 20:26 --

Someone
На лекциях, насколько я помню, такой теоремы не было, и понятия подобных множеств вроде бы то же. Правда там потом задача использующая понятие неподвижной точки, которого тоже вроде бы не было

-- 23.01.2026, 20:34 --

Someone в сообщении #1695441 писал(а):

Кстати, почему $A\neq\mathbb Q$?

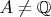
Потому что в $A$ отсутствуют: 1) Дроби соответствующие нецелым рациональным с чётными числителями; 2) Дроби с нечётными знаменателями

-- 23.01.2026, 20:40 --

Someone в сообщении #1715941 писал(а):

определение сечения в линейно упорядоченном множестве Вы знаете.

Этого (сечения) тоже не было. Это было в книге Э.Ландау, которая рекомендовалась Лектором к ознакомлению.

[mihaild]

cxzbsdhwert в сообщении #1715952 писал(а):

Так оба этих ограничения одновременны на биекцию в обе стороны

И понять, что вы имеете в виду, из них нельзя. Чтобы можно было понять, можно было бы написать, например, так.
Зададим функцию $f: X \to \mathbb Q$ таким образом: если $\frac{m}{2^n}$ несократима, то $f\left(\frac{m}{2^n}\right) = $ чему-то, зависящему от $m$ и $n$.
Тогда функция $g: \mathbb Q \to X$, заданная так: если $\frac{p}{q}$ несократима, то $g\left(\frac pq\right) = $ чему-то, зависящему от $p$ и $q$.
В таком виде было бы понятно, как заданы функции. И дальше можно доказывать нужные свойства.

cxzbsdhwert в сообщении #1715952 писал(а):

А если существует возрастающая биекция из $X$ в $\mathbb Q$, то можно взять композицию $\mathbb N \rightarrow X \rightarrow \mathbb Q$

Что значит эта запись?
Если бы была возрастающая биекция $f: X \to \mathbb N$ и возрастающая биекция $g: \mathbb N \to \mathbb Q$, то из них можно было бы сделать возрастающую биекцию $f \circ g: X \to \mathbb Q$.

cxzbsdhwert в сообщении #1715952 писал(а):

Но возрастающей биекции с $\mathbb N$ на $\mathbb Q$, насколько я понимаю, быть не может

Доказать можете? ИМХО хорошее упражнение на понимание определений.

cxzbsdhwert в сообщении #1715952 писал(а):

а порядок $\mathbb N \rightarrow X$ будет отличен?

Опять же, непонятно, о чем речь.
Вы знаете, как определяются функции, порядок и т.д. в терминах множеств? Вот старайтесь формулировать свои мысли так, чтобы их было понятно как изложить на языке множеств (непосредственно переводить на него обычно избыточно, но ИМХО полезно следить за тем, чтобы такой перевод был возможен).

cxzbsdhwert в сообщении #1715952 писал(а):

Формула выведенная по "диагональному методу" была на лекции

Это не диагональный метод, это "змейка".

cxzbsdhwert в сообщении #1715952 писал(а):

Но как это фактически учесть формульно? Может это не реально?

Реально, но нетривиально. И скорее не "учесть", а изначально строить биекцию иначе. Например, воспользовавшись тем, что и натуральное, и положительное рациональное число может быть представлено как произведение конечного числа простых в степенях, просто с немного разными ограничениями.

cxzbsdhwert в сообщении #1715952 писал(а):

На лекциях, насколько я помню, такой теоремы не было, и понятия подобных множеств вроде бы то же.

Ну если понятия не было, то додуматься самостоятельно сложно. Но после того, как формулировку теоремы вам указали - придумать её доказательство должно быть не очень сложно. Уж точно проще, чем построить требуемую биекцию в явном виде.

[cxzbsdhwert]

mihaild
Функция из $\mathbb Q$ в $X$ была такая: $\frac{m}{n}\in\mathbb Q \rightarrow \frac{m}{2^n}\in X$, но $\mathbb Q$ было ограничено так, что в нём нет дробей у которых сокращаемы: 1) числитель и знаменатель; 2) числитель и двойка в степени знаменателя (не знаю чем Вас не устроила формулировка таких ограничений в терминах НОД, ведь это то же самое).

Но это была функция не из всех рациональных в $X$ (а обратная по сути не была сюръекцией), поскольку пропущены рациональные представленные в виде дроби с чётной степенью, даже если эти дроби сами не сокращаемы, например $\frac{4}{5}$ исключена, поскольку $f(\frac{4}{5})=\frac{1}{2^4}$ и это привело бы к неинъективности в связи с $f(\frac{1}{4})=\frac{1}{2^4}=f(\frac{4}{5})$.

Тем не менее функция (с такими ограничениями) инъективна и монотонна, да?

Тогда можно попробовать изменить функцию, дополнив правило для чётных числителей. Важно заметить, что хотя не все рациональные из $\mathbb Q$ были задействованы, $X$ "охвачены" все. Можно попробовать их перераспределить.Что если так:

$f:\mathbb Q \rightarrow X$
$f(\frac{m}{n}) = \begin{cases} \frac{m}{2^{2n}},&\text{если НОД(m,2)=1}\\ \frac{m-1}{2^{2n-1}},&\text{иначе}\\ \end{cases}$

Для большего $m$ при этом, степень двойки в знаменателе меньше чем для такого же $n$, при $m-1$ прообраза, но при этом числитель обоих образов получается одинаковым, а значит возрастание вроде как сохраняется.
И ограничимся только натуральными $m$ и $n$ — для отрицательных $m$ всё симметрично, а ноль в ноль.

[Someone]

cxzbsdhwert в сообщении #1716030 писал(а):

но $\mathbb Q$ было ограничено так, что в нём нет дробей у которых сокращаемы: 1) числитель и знаменатель; 2) числитель и двойка в степени знаменателя (не знаю чем Вас не устроила формулировка таких ограничений в терминах НОД, ведь это то же самое).

Вам об этом писали, но Вы так и не поняли. Множество рациональных чисел $\mathbb Q$ не содержит никаких дробей, оно содержит рациональные числа. А дроби — это один из способов записи рациональных чисел. Причём, каждое рациональное число имеет бесконечно много записей в виде дроби.

cxzbsdhwert в сообщении #1715952 писал(а):

Someone
На лекциях, насколько я помню, такой теоремы не было, и понятия подобных множеств вроде бы то же. Правда там потом задача использующая понятие неподвижной точки, которого тоже вроде бы не было

Но задача, которую Вы пытаетесь решить, как раз и состоит в доказательстве этой теоремы. Несмотря на отсутствие явного определения подобия линейно упорядоченных множеств, подобных линейно упорядоченных множеств и формулировки теоремы. И это гораздо проще, чем пытаться сочинить явную формулу. Сочинить алгоритм, вычисляющий требуемую биекцию, я, может быть, и взялся бы, если бы мне это было очень нужно (но я не догадываюсь, зачем он нужен), а вот за формулу вряд ли взялся бы.
Подобие — это просто биекция, сохраняющая отношение порядка (возрастающая, другими словами).

cxzbsdhwert в сообщении #1715952 писал(а):

Someone в сообщении #1695441 писал(а):

Кстати, почему $A\neq\mathbb Q$?

Потому что в $A$ отсутствуют: 1) Дроби соответствующие нецелым рациональным с чётными числителями; 2) Дроби с нечётными знаменателями

Оба утверждения неверны: В вашей задаче $A$ — множество рациональных чисел, допускающих запись в виде $\frac m{2^n}$, где $m$ и $n$ — любые целые числа:

cxzbsdhwert в сообщении #1695435 писал(а):

Есть задача - доказать существование возрастающей биекции множества чисел вида $\dfrac{m}{2^n},\space m,n \in \mathbb{Z}$ в множество рациональных чисел $\mathbb{Q}$.

Числа, допускающие такую запись, называются двоично рациональными. От Вас требуют доказать, что множества рациональных чисел и двоично рациональных чисел подобны.

cxzbsdhwert в сообщении #1715952 писал(а):

Someone в сообщении #1715941 писал(а):

определение сечения в линейно упорядоченном множестве Вы знаете.

Этого (сечения) тоже не было. Это было в книге Э.Ландау, которая рекомендовалась Лектором к ознакомлению.

Это неважно. Для решения вашей задачи сечения не нужны. Сечение в линейно упорядоченном множестве $X$ — это просто упорядоченная пара $(A,B)$ непустых подмножеств множества $X$, удовлетворяющая условию $A\cup B=X$, и для любой пары элементов $a\in A$ и $b\in B$ выполняется неравенство $a<b$.
Например, один из способов построения множества действительных чисел состоит в использовании сечений в множестве рациональных чисел.

[cxzbsdhwert]

Someone в сообщении #1716057 писал(а):

Оба утверждения неверны

Имелось в виду в первом случае несокращаемые, во втором - нецелые.

Someone в сообщении #1716057 писал(а):

И это гораздо проще, чем пытаться сочинить явную формулу

Я всё-таки попробую ещё с последней функцией которую я предъявил выше

[ИСН]

cxzbsdhwert, бросьте искать явную формулу, ведь этого же не просят. Или не хотите - не бросайте, но относитесь к своим возможным кандидатам как к заведомо сломанным, и старайтесь показать, где именно они сломаны. (Обычно - везде и всюду. Так, последний вариант переводит $4,\,5,\,6$ в $\frac32,\,\frac54,\,\frac52$ - и куда делась монотонность?) Это fun, это Вам должно быть вполне доступно, и тогда от этого всё-таки будет толк. А от реальной формулы - нет. (Здесь, кажется, все молчаливо сговорились Вам её не сообщать, так что я тоже не буду.)

[Someone]

cxzbsdhwert в сообщении #1716067 писал(а):

Someone в сообщении #1716057 писал(а):

Оба утверждения неверны

Имелось в виду в первом случае несокращаемые, во втором - нецелые.

Откуда я могу знать, что у Вас "имелось в виду"? И даже в этом случае оба утверждения неверны. По условию $m,n\in\mathbb Z$, а не $\mathbb N$, как Вы, вероятно, думаете. Например, заданному множеству $A$ принадлежит число $\frac 1{2^{-1}}=\frac 21$. Из определения множества $A$ никак не следует, что оно не содержит целых чисел, и Вы, решая задачу, не имеете права вводить дополнительные условия, отсутствующие в задаче.

cxzbsdhwert в сообщении #1716067 писал(а):

Someone в сообщении #1716057 писал(а):

И это гораздо проще, чем пытаться сочинить явную формулу

Я всё-таки попробую ещё с последней функцией которую я предъявил выше

Вам, по-моему, уже сказали, что последняя функция тоже не годится. Не говоря уже о том, что Вы, похоже, плохо себе представляете, какие рациональные числа входят в $A$, а какие — нет.

[cxzbsdhwert]

Итак, функция (пришлось ещё уточнить знаменатель, иначе пропускаются целые образы, и ещё числитель для нечётного случая, для соблюдения монотонности):
$f:\mathbb Q \rightarrow X$
$f(\frac{m}{n}) = \begin{cases} \frac{2m-2}{2^{2n-1}},&\text{если НОД(m,2)=1}\\ \frac{m-1}{2^{2n-2}},&\text{иначе}\\ \end{cases} m,n\in\mathbb N$
Обратная ($X$ - мн-во чисел вида $\frac{m}{2^n}$, рассматриваем только несократимые, но в том числе целые)
$f^{-1}:X \rightarrow \mathbb Q$
$f(\frac{m}{2^n}) = \begin{cases} \frac{(m+2)/2}{(n+1)/2}, &\text{если НОД(n,2) $= 1$ }\\ \frac{m+1}{(n+2)/2}, &\text{иначе}\\ \end{cases} m\in\mathbb N,n\in \mathbb N\cup\{0\}$

Вроде бы эта функция инъективна и сюръективна.
Необходимо показать монотонность. Наверное придётся рассматривать три или даже четыре случая: два случая гомогенных по параметризации аргументов и один (но может и два) и гетерогенных:

(Оффтоп)

1) $f(x_1)>f(x_2)$, при $x_1>x_2$, если у $x_1$ и $x_2$ числитель нечётный
2) $f(x_1)>f(x_2)$, при $x_1>x_2$, если у $x_1$ и $x_2$ числитель чётный
3) $f(x_1)>f(x_2)$, при $x_1>x_2$, если у $x_1$ числитель чётный, а у $x_2$ числитель нечётный
4) Ну и, если 3 недостаточно, то $f(x_1)>f(x_2)$, при $x_1>x_2$, если у $x_1$ числитель нечётный, а у $x_2$ числитель чётный

ИСН опередил с выявлением немонотонности предыдущей функции, но предыдущая функция, повторюсь была вообще не биекцией. После устранения (вроде) несюръективности, и внесения изменения в числитель ну по крайней мере для предъявленного Вами примера уже монотонность соблюдается:

(Оффтоп)

$1\rightarrow \dfrac{0}{2} = 0 <$
$2\rightarrow \dfrac{1}{1} = 1 <$
$3\rightarrow \dfrac{4}{2} = 2 <$
$4\rightarrow \dfrac{3}{1} = 3 <$
$5\rightarrow \dfrac{8}{2} = 4 <$
$6\rightarrow \dfrac{5}{1} = 5 <$
$7\rightarrow \dfrac{12}{2} = 6$

Для случайных с отличными от единицы дробей монотонность выполнилась: $f(\frac{5}{2})>f(\frac{4}{3})$. Но строгое доказательство по всем четырём пунктам ещё ждёт.

ИСН в сообщении #1716074 писал(а):

относитесь к своим возможным кандидатам как к заведомо сломанным

Да, извините конечно что обременяю всех промежуточными результатами, невыдержующих элементарных проверок.

-- 24.01.2026, 17:15 --

Someone в сообщении #1716079 писал(а):

какие рациональные числа входят в $A$, а какие — нет.

Да, я вроде полагал всё это время что в $X$ (так я его назвал) нет чётных целых. Сейчас гляну на последнюю функцию.
Да, с целыми чётными в $X$ есть проблема в плане сюръективности.

Возможно стоит в числителе случая нечётного $m$ вычитать $2$ из $2m$, а не $1$. Пусть будет так, отредактирую

[cxzbsdhwert]

Функция не монотонна, методом перебора установил

[Someone]

cxzbsdhwert в сообщении #1716092 писал(а):

Да, я вроде полагал всё это время что в $X$ (так я его назвал) нет чётных целых.

$X$ — это множество так называемых двоично-рациональных чисел, которые в двоичной системе счисления записываются конечной двоичной дробью.
Вы же знаете, что такое десятичная дробь?
Десятичные дроби бывают конечными (когда после десятичной запятой имеется только конечное число ненулевых цифр: $27{,}3590057$, например) и бесконечными (когда после десятичной запятой идёт бесконечный "хвост", содержащий бесконечное множество ненулевых цифр).
Конечные десятичные дроби образуют множество десятично-рациональных чисел. Но не все рациональные числа являются десятично-рациональными. Например, $\frac 13=0{,}33333333\ldots=0{,}(3)$ не является десятично-рациональным числом. Последняя запись означает бесконечную периодическую дробь с периодом, состоящим из одной цифры "$3$". Период может содержать больше одной цифры и начинаться не сразу после запятой: $\frac{2377}{2125}=1,118(5882352941176470)$.
Тут есть одна "ловушка": десятично-рациональное число имеет две различные записи в виде десятичной дроби, одна из которых является конечной, а другая — бесконечной периодической с периодом, состоящим из одной цифры "$9$": $27{,}3590057=27{,}359005699999\ldots=27{,}3590056(9)$. Обычно по умолчанию используется запись с конечной дробью.
Каждое рациональное число имеет запись в виде периодической десятичной дроби (если зачем-то нужно, можно конечную десятичную дробь считать периодической с периодом, состоящим из одной цифры "$0$"). И наоборот: каждая периодическая десятичная дробь задаёт рациональное число.

Такая же картина — для двоичных дробей.

[cxzbsdhwert]

Someone
Если бы я не знал того что Вы написали я бы наверное здесь не сидел. Я не знал (и то, скорее забыл) только что период должен начинаться почему-то не с первого разряда. Я понимаю что десятичная дробь $2.7$ это составная или как там она называется дробь $2\frac{7}{10}=2+\frac{7}{10}$. Я понимаю и могу доказать что $0.9(9)=1$. Я понимаю что рационально число представимо в виде конечной или бесконечной периодической дроби (это вроде определение, хотя может и доказуемо). Я понимаю что иррациональное число представимо в виде бесконечной непереодичной дроби.

Я ранее не думал об этом но понимаю что рациональное число можно представить "через точку" и в виде дроби другой "характеристики", например $2$. То есть что бы представление ограничилось вычетами (о которых я пока только слышал, поскольку ни на Теории чисел ни на Алгебре этого ещё не было) двойки, ну то есть нулями и единицами? Типо $\frac{3}{7}=\frac{6/7}{2}$ и дальше это как-то представляется как $0.01001101...$?
Это к чему вообще? Это должно быть использовано в связке с Теоремой, которую Вы упомянули?