Доказать несчётность отрезка теоремой Бэра

[warlock66613]

cxzbsdhwert в сообщении #1713482 писал(а):

Конечно, если они оба несчётны.

Нет, это элементарно доказывается без обращения к несчётности. Например, пусть отрезок $[a, b]$ и интервал $(c, d)$ таковы, что $a < d$, $b < d$, $c > a$. Тогда чтобы они имели пересечение необходимо чтобы $b > c$. Но раз $c < b < d$, то это значит, что точка отрезка $b$ принадлежит интервалу $(c, d)$, то есть является точкой пересечения. Также рассмотрим точку $x = \frac {c+b} 2$. Так как $x < b$ и $x > c > a$, то эта точка принадлежит отрезку. Так как $x > c$ и $x < b < d$, то она также принадлежит интервалу. Значит это вторая точка пересечения. И так можно рассмотреть все варианты взаиморасположения отрезка и интервала.

[cxzbsdhwert]

warlock66613 в сообщении #1713478 писал(а):

Тогда этот отрезок можно представить в виде объединения одноэлементных множеств

А это вторая вещь о которой мы тут пятую страницу спорим. Давайте, ладно, уберём слово "представление". Переформулируем так:
"Выражением отрезка может быть объединение одноэлементных множеств". "Выражение" же строгое математическое, даже логическое понятие, составная часть высказывания.

Ну а что значит (это всё-таки называется не квантор, а - ) предикат "может быть". Ну, только Вам известно, поскольку Вы его использовали (точнее использовали "можно"), но я думаю Вы и все остальные согласятся с тем, что это Ваше утверждение можно привести к более строгой форме:

"отрезок (полагая что он нбчс) является объединением нбчс набора только одноэлементных множеств ИЛИ объединением нбчс набора не только одноточечных нбчс множеств".
Согласны? Вот @skobar категорически нет, из-за чего спор на 5 страниц.

Это утверждение следствие из отрицания, в рамках доказательство от обратного. Показав ложность этого следствия, покажем и ложность отрицания.
Но, если Вы согласны со строгой формулировкой, Вы не можете не согласится что тогда ложность следствия в виду того что оно является дизъюнкцией достигается ложным только в том случае, если к противоречию приводит И одноточечный вариант (Вы это противоречие, пускай, предъявили) И неодноточечный.
А протеворечивости только одноточечного варианта при непротиворечивости неодноточечного не достаточно для ложности всего следствия и изначального отрицания.
Верно?

-- 28.12.2025, 17:06 --

warlock66613 в сообщении #1713483 писал(а):

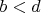
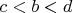
Нет, это элементарно доказывается без обращения к несчётности. Например, пусть отрезок $[a, b]$ и интервал $(c, d)$ таковы, что $a < d$, $b < d$, $c > a$. Тогда чтобы они имели пересечение необходимо чтобы $b > c$. Но раз $c < b < d$, то это значит, что точка отрезка $b$ принадлежит интервалу $(c, d)$, то есть является точкой пересечения.

Да, абстрагируясь от природы отрезка, ну если только не полагать самые абсурдные варианты того что мы считаем отрезком, то одну точку пересечения Вы предъявили.

warlock66613 в сообщении #1713483 писал(а):

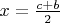
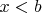
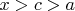
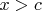
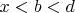
Также рассмотрим точку $x = \frac {c+b} 2$. Так как $x < b$ и $x > c > a$, то эта точка принадлежит отрезку. Так как $x > c$ и $x < b < d$, то она также принадлежит интервалу. Значит это вторая точка пересечения. И так можно рассмотреть все варианты взаиморасположения отрезка и интервала.

А вот это накладывает существенные ограничения на то, чем отрезок является.
Вы скажете: "нас интересует нбчс счётное представление отрезка - значит рациональный отрезок $[a,b]=\{x\in\mathhb Q:a\leq x \leq b\}$ подойдёт."
Я спрошу: "почему не подойдёт нбчс вообще например конечное множество?".
Вы ответите - "потому что по определению отрезка, даже не полагая его несчётным, в нём должны быть все $x$ из $\mathbb R$ такие что и т.д. В конечном множестве будут не все, поэтому оно точно не подойдёт".
Хорошо, а в рациональном, который "подойдёт", что, разве, "все" будут? Да точно так же нет.

Тогда почему такой рациональный отрезок, на котором действительно не получится взять одноэлементное пересечение с интервалом Вы рассматриваете, а конечный отрезок не рассматриваете, хотя они оба не удовлетворяют определению "настоящего" отрезка.

То есть тут по-моему тогда противоречие сразу на этапе отрицания, и следствия никакую роль не играют.
Но тогда тут второй вопрос, который я задал в самом первом сообщении - правильно ли я понимаю, что рассматривая одноэлементный случай, чем и ограничился Лектор, Теоремой Бэра тут ничего не доказывается?

А вот рассматривая неодноэлементный нбчс случай, мы можем полагать, что в том числе иррациональные будут в объединении, и тогда уже по Теореме Бэра сможем утверждать что найдётся пересечение с вещественным а значит несчётным интервалом, а значит в виду как раз несчётности интервала, но счётности $F_n$, пересечение "потеряет" иррациональные точки.
А по предположению от противного они в $F_n$ есть. Вот и противоречие, вот и Теорема Бэра.

[skobar]

cxzbsdhwert в сообщении #1713472 писал(а):

Не лишнее и не ненужное. Почему - написано дальше в сообщении.

Лишнее и ненужное. У вас в сообщении написана, извините, чушь. Вам предоставлено цельное законченное доказательство без ваших фантазий.

cxzbsdhwert в сообщении #1713472 писал(а):

Давайте будем более конструктивны.

Давайте.

cxzbsdhwert в сообщении #1713472 писал(а):

Если в моём сообщении, показывающем противоречие в Ваших рассуждениях, есть противоречие, пожалуйста укажите на него, и докажите что и чему оно противоречит.

Такого сообщения нет.

Вообще, если вы считаете себя умнее лектора и докторов наук на этом форуме, то что вы здесь делаете? Зачем спрашивать кого-то, если вы сами лучше знаете?

[warlock66613]

cxzbsdhwert в сообщении #1713485 писал(а):

А это вторая вещь о которой мы тут пятую страницу спорим.

И совершенно напрасно, так как всё обсуждаемое не предмет для спора.

cxzbsdhwert в сообщении #1713485 писал(а):

Давайте, ладно, уберём слово "представление".

Можно заменить на "является" или "равен".

cxzbsdhwert в сообщении #1713485 писал(а):

это Ваше утверждение можно привести к более строгой форме

Это не "более строгая форма", это попросту другое утверждение, которое хоть и верное (тривиально потому что верна его первая часть до "или"), но совершенно бесполезное.

cxzbsdhwert в сообщении #1713485 писал(а):

Верно?

Верно, поэтому мы не используем в доказательстве утверждение

cxzbsdhwert в сообщении #1713485 писал(а):

отрезок (полагая что он нбчс) является объединением нбчс набора только одноэлементных множеств ИЛИ объединением нбчс набора не только одноточечных нбчс множеств

а используем другое утверждение: не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств. Точка, никаких "или".

Кстати, верно также и утверждение "не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств И также является объединением не более чем счётного набора неодноэлементных множеств" -- не с "ИЛИ" а с "И", но это опять же неважно для доказательства.

cxzbsdhwert в сообщении #1713485 писал(а):

Вы скажете: "нас интересует нбчс счётное представление отрезка - значит рациональный отрезок $[a,b]=\{x\in\mathhb Q:a\leq x \leq b\}$ подойдёт."

Нет, я такого не скажу. "Рациональный отрезок" -- это не отрезок. Обычное определение отрезка -- это $[a,b]=\{x\in\mathbb R:a\leqslant x \leqslant b\}$, им и нужно пользоваться.

[cxzbsdhwert]

warlock66613 в сообщении #1713487 писал(а):

используем другое утверждение: не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств. Точка, никаких "или".

Ваше утверждение верно только для отрезка, полагая его счётным, или для любого нбчс множества?
То есть - "любое не более чем счётное множество является объединением не более чем счётного набора одноэлементных множеств. Точка, никаких "или"."?

[warlock66613]

cxzbsdhwert в сообщении #1713492 писал(а):

Ваше утверждение верно только для отрезка, полагая его счётным, или для любого нбчс множества?

Для любого.

[cxzbsdhwert]

Поскольку, если предметно, но объёмно, показать противоречия в Ваших рассуждения, то Вы многие из них просто оставляете без внимания, не желая ни согласиться ни привести контраргументы, то я придумал ёмкое доказательства противоречия в Вашем рассуждении, которое уже не сможет "затеряться" между строк:

Рассмотрим саму Теорему Бэра, как её дал Лектор, вне доказательства несчётности отрезка: "Пусть F - непустое замкнутое подмн. $\mathbb R$ и $F=\cup_nF_n$ - нбчс объединение, $F_n$ - замкнуты. Тогда $\exists (N \text{и} (a,b)): F\cap(a,b)\neq \emptyset$ и $F\cap (a,b)\subset F_N$"

Я утверждаю 5 страниц, что представление $F$ важно, и необходимо рассматривать разные представления.
Вы утверждали обратное, в частности, пишите что никаких представлений нет, и (уточнив что это верно для любого нбчс множества а не только отрезка):

warlock66613 в сообщении #1713487 писал(а):

используем другое утверждение: не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств. Точка, никаких "или".

Тогда, Теорема Бэра утверждает что пересечение с интервалом, принадлежащее $F_n$ всегда одноточечно (никаких "или"), поскольку по Вашему утверждению $F=\cup_n F_n$ будучи нбчс, как любое нбчс множество, как Вы заявили - является объединением не более чем счётного набора одноэлементных множеств и никаких "или".

То есть по Теореме Бэра с Вашим утверждением не существует такого состоящего из более одной точки пересечения интервала с нбчс(замкнутым) множеством $F$, чтобы одному из множеств, объединением которых является это нбчс (замкнутое) множество $F$, принадлежало бы это пересечение, поскольку $F$, будучи нбчс - объединение одноточечных?

[warlock66613]

cxzbsdhwert в сообщении #1713496 писал(а):

То есть по Теореме Бэра с Вашим утверждением не существует такого

Нет, такого не следует, так как из того что некоторое множество является объединением одноэлементных множеств не следует, что оно не является объединением неодноэлементных множеств.

[cxzbsdhwert]

warlock66613 в сообщении #1713497 писал(а):

cxzbsdhwert в сообщении #1713496 писал(а):

То есть по Теореме Бэра с Вашим утверждением не существует такого

Нет, такого не следует, так как из того что некоторое множество является объединением одноэлементных множеств не следует, что оно не является объединением неодноэлементных множеств.

Чудесно, а вот это утверждение же тоже верно не только для отрезка но и всякого нбчс множества?

warlock66613 в сообщении #1713487 писал(а):

Кстати, верно также и утверждение "не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств И также является объединением не более чем счётного набора неодноэлементных множеств" -- не с "ИЛИ" а с "И", но это опять же неважно для доказательства.

[warlock66613]

cxzbsdhwert в сообщении #1713498 писал(а):

а вот это утверждение же тоже верно не только для отрезка но и всякого нбчс множества?

Для любого, содержащего по крайней мере 2 элемента.

[cxzbsdhwert]

warlock66613 в сообщении #1713499 писал(а):

Для любого, содержащего по крайней мере 2 элемента.

Ну вот.
Тогда из Ваших суждений:

warlock66613 в сообщении #1713487 писал(а):

любой не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств. Точка, никаких "или".

и

warlock66613 в сообщении #1713487 писал(а):

любой не более чем счётный отрезок является объединением не более чем счётного набора одноэлементных множеств И также является объединением не более чем счётного набора неодноэлементных множеств, но это опять же неважно для доказательства.

,по Теореме Бэра следует что в любом замкнутом (нбчс) множестве один и тот же интервал будет иметь одновременно только одну И не только одну точку пересечения.
Противоречие.
При чём, как Вы справедливо указали, и я это подчеркнул, к противоречию Теореме Бэра Ваши рассуждения приводят вне контекста доказательства несчётности отрезка и каких-либо отрицаний, расммотрений "от обратного".

[warlock66613]

cxzbsdhwert в сообщении #1713500 писал(а):

по Теореме Бэра следует что в любом замкнутом (нбчс) множестве один и тот же интервал будет иметь одновременно только одну И не только одну точку пересечения

И как же это следует? Применяя теорему Бэра один раз вы можете вывести существование интервала такого, что он имеет одну точку пересечения с замкнутым множеством. Применяя теорему Бэра снова вы можете вывести существование интервала такого, что он имеет не одну точку пересечения с тем же множеством. Но вы никак не можете доказать что это один и тот же интервал.

[skobar]

Кажется, я начинаю лучше понимать, что у TC в голове :)
Среди прочего, похоже, что TC не осознает, что интервал, существование которого утверждает следствие из теоремы Бэра, зависит не только от замкнутого множества $F$, но и от представления $F$ в виде объединения замкнутых множеств $F=\cup_n \ F_n$. Если взять другое представление $F$, то для этого другого представления интервал будет уже другим.

[cxzbsdhwert]

Ой, как я ещё тут не увидел. Можем мы на секунду отвлечься?

warlock66613 в сообщении #1713478 писал(а):

Пусть существует отрезок, который является не более чем счётным множеством. $\leftarrow$ Вот я предъявляю вам отрезок.

Тогда этот отрезок можно представить в виде объединения одноэлементных множеств: $\{x_1\} \cup \{x_2\} \cup \{x_3\} \cup \ldots$. Тогда по теореме Бэра существует пересекающийся с отрезком интервал, пересечение которого с этим отрезком содержится ($\subseteq$) в некотором $\{x_i\}$. $\leftarrow$ Вот я предъявляю интервал.

Раз пересечение отрезка и интервала содержится в одноэлементном множестве, то оно состоит ровно из одной точки. $\leftarrow$ Вот я доказал что пересечение отрезка и интервала состоит из одной точки.

В то же время, верно, что любой отрезок и любой интервал, если только пересекаются, то пересекаются как минимум в двух точках. Значит и наши конкретные отрезок и интервал пересекаются минимум в двух точках. $\leftarrow$ Вот я доказал, что пересечение всё того же отрезка и всё того же интервала состоит минимум из двух точек.

Получаем противоречие.

Так через эти же рассуждения можно доказать несчёность подмножества рациональных чисел, то есть, точно счётного множества.
Ну например $X=\{x\in \mathbb Q: 0\leq x \leq 1\}$, или $X=\{\frac{1}{n},\frac{1}{2n},...|n\in Q, n>1\}$. Подставьте в своё сообщение вместо слова "отрезок", такое множество $X$, и по Вашим рассуждениям окажется, что оно несчётно.

[warlock66613]

cxzbsdhwert в сообщении #1713503 писал(а):

Так через эти же рассуждения можно доказать несчёность подмножества рациональных чисел, то есть, точно счётного множества.

Нет, только множества, которое а) является замкнутым и б) пересечение которого с любым интервалом либо пусто, либо содержит минимум две точки.