Элементарная алгебра для отстающих

[horda2501]

Это, конечно, опечатка. Если по всем правилам, то ответ будет $x=-\frac{5\pi}{4}+/-2\pi k$. Вопрос посерьёзнее: почему же $\sin sin x + \sin x= \sin 2x$ неверное равенство, если ответ из него правильный получается?

[wrest]

horda2501 в сообщении #1712792 писал(а):

Если по всем правилам, то ответ будет $x=-\frac{5\pi}{4}+/-2\pi k$.

Если имеется в виду ответ к упражнению

horda2501 в сообщении #1712760 писал(а):

1) $\sin(x+2\pi)+\sin(x-4\pi)=1$

То ваш ответ $x=-\frac{5\pi}{4}+/-2\pi k$ -- неверный. Возьмите калькулятор, подставьте ответ и убедитесь, наконец!

-- 18.12.2025, 20:59 --

horda2501 в сообщении #1712792 писал(а):

Вопрос посерьёзнее: почему же $\sin sin x + \sin x= \sin 2x$ неверное равенство, если ответ из него правильный получается?

Это только в вашей, альтернативной, вселенной, где ещё не придумали калькуляторы. Такие уж там у вас правила

[horda2501]

С ответом, да, правильно $\frac{\pi}{6}$ и $\frac{5\pi}{6}$. Я понимаю эти соответствия, просто не выучила их ещё наизусть. Что мне действительно непонятно, так это $\sin x + \sin x= \sin 2x$. Почему не равно? Потому что корректна запись $\sin x + \sin x= 2 \sin x$ или причина другая?

[ozheredov]

horda2501 в сообщении #1712804 писал(а):

Что мне действительно непонятно, так это $\sin x + \sin x= \sin 2x$. Почему не равно?

Патамушта синус - хвункция НЕЛИНЕЙНАЯ!!!!

Почему $x^2 + x^2 \neq (2x)^2$?

[horda2501]

Я затрудняюсь ответить развёрнуто на этот вопрос, однако, очевидно, что это неверно потому что когда при складывании возникает $2$, указывающее на то, что сложено два одинаковых слагаемых, оно не возводится в степень, так как для этого нет соответствующего действия, нет причины для этого. А для объединения двух слагаемых с одинаковым основанием степени и показателем степени есть причина (действие сложения). Это сейчас не очень просто всё сразу внимать, когда данные функции чисто алгебраические. То есть, я ещё их для исследования физических процессов не применяла и это чистая абстракция. Поэтому на данном этапе воспринимается как $\sin x + \sin x$ => сложи два $x$ и воспользуйся действием $\sin$, то есть, тогда узнаешь что же это за значение $x$ на числовой окружности. Если синус $\frac{1}{2}$, то ему будет соответствовать то или иное значение $x$ как числа на числовой окружности.

Где ошибка в понимании? (Её нахождение затруднено тем, что такой ход мысли приводит к ответу в обоих случаях).

[Dedekind]

horda2501 в сообщении #1712812 писал(а):

$\sin x + \sin x$ => сложи два $x$ и воспользуйся действием $\sin$

Наоборот. Воспользуйся действием синус 2 раза и сложи результат.

[Booker48]

horda2501 в сообщении #1712812 писал(а):

Где ошибка в понимании? (Её нахождение затруднено тем, что такой ход мысли приводит к ответу в обоих случаях).

Но в одном случае ответ неправильный, что проверяется подстановкой решения.

[horda2501]

Dedekind в сообщении #1712814 писал(а):

horda2501 в сообщении #1712812 писал(а):

$\sin x + \sin x$ => сложи два $x$ и воспользуйся действием $\sin$

Наоборот. Воспользуйся действием синус 2 раза и сложи результат.

Не поняла. По отношению к чему нужно применять действие $\sin$ в изначальном выражении $\sin x + \sinx = 1$? То есть, какое следующее преобразование? Когда следующее выражение $\sin 2x=1$, то ты отделяешь действие $\sin$ и оно выглядит как $\sin$ для $2x = 1$. А дальше уже выполняешь нахождение соответствия. Мол, синус $\frac{1}{2}$ для какого $x$ на числовой окружности? Всё кажется понятным, не могу внять где ошибка.

[wrest]

Booker48 в сообщении #1712815 писал(а):

Но в одном случае ответ неправильный, что проверяется подстановкой решения.

По всей видимости, ТС не имеет калькулятора либо имеет но не умеет пользоваться. Для ТС, как мне кажется, алгебра это абстрактная наука про буковки и синтаксические правила их трансформации , не имеющая отношение к числам.
Я за последние страницы ЧЕТЫРЕ раза предложил воспользоваться калькулятором, но безуспешно.

[Booker48]

horda2501 в сообщении #1712818 писал(а):

Dedekind в сообщении #1712814 писал(а):

horda2501 в сообщении #1712812 писал(а):

$\sin x + \sin x$ => сложи два $x$ и воспользуйся действием $\sin$

Наоборот. Воспользуйся действием синус 2 раза и сложи результат.

Не поняла. По отношению к чему нужно применять действие $\sin$ в изначальном выражении $\sin x + \sinx = 1$? То есть, какое следующее преобразование? Когда следующее выражение $\sin 2x=1$, то ты отделяешь действие $\sin$ и оно выглядит как $\sin$ для $2x = 1$. А дальше уже выполняешь нахождение соответствия. Мол, синус $\frac{1}{2}$ для какого $x$ на числовой окружности? Всё кажется понятным, не могу внять где ошибка.

По отношению к неизвестной $x$. Берёте от неё функцию синус, потом делаете это ещё один раз, потом складываете полученные результаты - и получается $2\sin x$. Вас же не удивило, что именно так происходит в случае, если функция $x^2$.

[Neznajka_]

horda2501 в сообщении #1712772 писал(а):

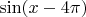
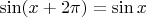
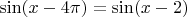
Хм, вот с $\sin(x-4\pi)$ мне как раз и не понятно ничего. Плюс или минус $2\pi k$ значит обращение $k$ раз и возвращение в исходную точку. То есть, можно поставить знак равенства в $\sin(x+2\pi)=\sin x$, правильно? Тогда в $\sin(x-4\pi)=\sin (x-2)$? (Очевидно, что эта запись смысла не имеет, но это всё что я сейчас могу ).

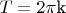
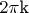
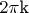
График синуса повторяется каждые $T=2\pi$k$ ($k$-целое). Из этого следует, что если "отойти" от начала координат на длину $2\pi$k, то "окажетесь" в точке, с которой график изменяется точно также, как начиная с точки $(0;0)$. Ну и значение функции в этой точке будет тоже равным нулю. 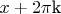Если отойти на произвольную длину $x$ от начала координат, а потом оттуда отойти на $2\pi$k, то аналогично в данной точке ($x+ 2\pi$k$) значение функции будет равно значению в точке $x$. Поэтому и получается $sin(x+ 2\pi$k)$$=sin(x)$. 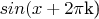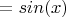Всё это, собственно, следует из определения периода функции.
А ещё есть теоремы ("правила", "формулы") приведения, которые вроде как по-нормальному должны были проходиться перед тригонометрическими функциями. По ним тоже можно прийти к равенству $sin(x+ 2\pi)$$=sin(x)$.

horda2501 в сообщении #1712812 писал(а):

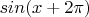
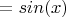
Поэтому на данном этапе воспринимается как $\sin x + \sin x$ => сложи два $x$ и воспользуйся действием $\sin$, то есть, тогда узнаешь что же это за значение $x$ на числовой окружности. Если синус $\frac{1}{2}$, то ему будет соответствовать то или иное значение $x$ как числа на числовой окружности.

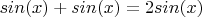
Синус от числа икс чему-то равен, верно? Значит если сложить два значения синуса от икс, получится в два раза по модулю больше. Т.е. Вы просто "приводите подобные слагаемые", получая $sin(x) + sin(x) = 2sin(x)$.

[ozheredov]

wrest в сообщении #1712819 писал(а):

Для ТС, как мне кажется, алгебра это абстрактная наука про буковки и синтаксические правила их трансформации

И в чём она не права?

wrest в сообщении #1712819 писал(а):

не имеющая отношение к числам.

Алгебра не имеет никакого отношения к числам. Это числа имеют какое-то отношение к алгебре, но в данном случае это по барабану.

wrest в сообщении #1712819 писал(а):

Я за последние страницы ЧЕТЫРЕ раза предложил воспользоваться калькулятором

То есть, сумма синусов не равна синусу двойного аргумента, потому что вонючая железка так показывает на своём экранчике? Завтра я спаяю на АРДУИНЕ вонючую железку с радикально противоположными правилами вывода, и математика поменяется. Кстати, ТС знает, что не равна. Она спрашивает, почему не равна.

[Dedekind]

horda2501
Это просто приоритет выполнения операций. Когда записано $x^2 + x^2$, сначала нужно возвести $x$ в квадрат, потом еще раз, и только потом сложить. А не сначала сложить, а потом возвести в квадрат. В результате получается $2x^2$, а не $(2x)^2$. С синусами $\sin x + \sin x$ то же самое: сначала вычисляется один синус, потом второй, потом результат складывается. В результате получается $2\sin x$, а не $\sin (2x)$.

[wrest]

ozheredov в сообщении #1712830 писал(а):

И в чём она не права?

В том что ТС, увы, не Гильберт, который говорил что вместо плоскостей, точек и прямых можно говорить про столы, стулья и пивные кружки.
Подход к изучению алгебры как, скажем, какого-то иностранного языка, как раз и приводит к выводам типа $\sin x + \sin x=\sin 2x$ или

ozheredov в сообщении #1705752 писал(а):

завидной регулярностью лепите $(a+b)^2 = a^2 + b^2$?

-- 19.12.2025, 10:44 --

(ozheredov)

ozheredov в сообщении #1712830 писал(а):

То есть, сумма синусов не равна синусу двойного аргумента, потому что вонючая железка так показывает на своём экранчике?

зачем этот флейм тут? я пас.

[ozheredov]

wrest в сообщении #1712836 писал(а):

В том что ТС, увы, не Гильберт, который говорил что вместо плоскостей, точек и прямых можно говорить про столы, стулья и пивные кружки.

Именно: нужно сразу объяснять, что математика абстрактная наука, не имеющая ни малейшего отношения к калькуляторам, яблокам у Саши и Маши и прочим предметам из "объективной реальности" (с). Любые бытовые вещи могут иметь отношение к математике, но эта любовь сугубо односторонняя, осуществляемая через некую абстрактную сущность под названием "модель". Дети успешно изучают шахматы, хотя прекрасно понимают, что никакая "объективная реальность" (с) не подскажет им правила, по которым ходит конь (в отличие от яблок Саши и Маши, которые ЯКОБЫ подсказывают (на самом деле нет), что 2+3=5). Более того, вместо коня можно поставить на доску пивную кружку пуговицу (если конь потерялся), и ни у кого не возникнет никаких вопросов. Калькулятор говорит, что два синуса икс не равно синусу от двух иск? А если я переключу его в двоичный режим, то $1 + 1 = 10$.