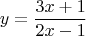Почему это происходит?
То есть вас не решение задачи смущает, а красивые соотношения? А решение знаете?
Может, вам проще побольше букв ввести? Попробую все-таки один раз показать, хотя, может и правда пока лучше отложить...
Вот функция
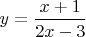
, она переводит

в число
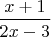
. А мы хотим, видя это число, понять, из какого

оно получилось.
Например,
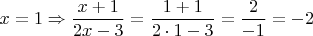
А теперь представьте, что вы знаете только ответ, т.е.

. Чему был равен

, из которого он получился? Чтобы узнать, надо решить уравнение,
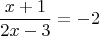
.
Дальше алгебра, умножаем левую и правую часть на
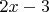
:
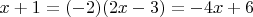
Переносим иксы на одну сторону, а свободные члены на другую:
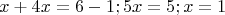
Видите, мы получили то самое значение, с которого начинали!
Для значения

аргумент мы нашли. Но только невозможно же это проделывать с каждым числом! Поэтому вместо

берут какой-то параметр. Пусть, например,

. Получаем
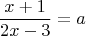
.
Умножаем левую и правую часть на
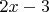
:
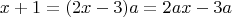
Переносим члены с

налево, остальные -- направо:
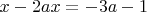
откуда
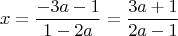
Вот, выразили

через значение функции. Получили значение (прежнего) аргумента через "прежнее" значение.
А теперь мы можем считать, что

-- это аргумент новой функции, в

-- её значение! Ну,и обозначить их, как принято,

и

: