Интерпретации квантовой механики

[realeugene]

B3LYP в сообщении #1700519 писал(а):

Изобретатель квантовых компьютеров Петер Шор

Вы действительно думаете, что он не овладел в совершенстве формализмом квантовой механики прежде, чем занялся околофилософскими рассуждениями?

[EUgeneUS]

B3LYP в сообщении #1700519 писал(а):

Изобретатель квантовых компьютеров Петер Шор

Питер Шор не является изобретателем квантовых компьютеров.

[B3LYP]

realeugene в сообщении #1700545 писал(а):

B3LYP в сообщении #1700519 писал(а):

Изобретатель квантовых компьютеров Петер Шор

Вы действительно думаете, что он не овладел в совершенстве формализмом квантовой механики прежде, чем занялся околофилософскими рассуждениями?

Я ничего не имею против формализма квантовой механики. Но и рассуждения тоже нужны.

[пианист]

(Оффтоп)

B3LYP в сообщении #1700550 писал(а):

Я ничего не имею против формализма квантовой механики. Но и рассуждения тоже нужны.

Представил себе картину: психическая атака белых из фильма "Чапаев", а голос диктора комментирует: "Это физики. Они не умеют рассуждать. У них есть только формализм."
:)

[warlock66613]

Утундрий в сообщении #1698600 писал(а):

Наивный вопрос: а как у него там с энтропией?

Если система закрытая, то энтропия растёт в обе стороны от особой (начальной) точки. Если открытая, то может и уменьшаться за счёт сброса лишней энтропии в окружающую среду.

(Я тут немного болел, немного работал, немного думал над вопросом об энтропии. Постараюсь теперь всем ответить кто что-то мне писал пока меня не было.)

[B3LYP]

warlock66613 в сообщении #1709630 писал(а):

Я тут немного болел, немного работал, немного думал над вопросом об энтропии. Постараюсь теперь всем ответить кто что-то мне писал пока меня не было.

С возвращением!
А можно я продублирую свой пост:

Цитата:

И вот такой вопрос. Есть известные эксперименты КМ - кот Шредингера (точнее друг Вигнера) и эксперимент Элитсура-Вайдмена с бомбами. Я могу истолковать эти эксперименты в рамках копенгагенской и многомировой интерпретаций, с ними становится чуть яснее. А может кто-нибудь тут истолковать эти эксперименты в рамках новых интерпретаций, например транзакционной или TSVF?

[warlock66613]

Если на пальцах, то в рамках TSVF всё трактуется так же, как в ММИ, только есть вторая волновая функция, которая маркирует определённый "мир", а точнее "ветвь" как существующую. Поэтому кот всё время жив (либо мёртв) и друг Вигнера тоже не находится в суперпозиции, а находится в определённом состоянии. Если не на пальцах, то надо для начала разобраться с тем как в TSVF трактуется измерение -- я приводил подробные выкладки на форуме, а тогда всё станет ясно и с другом Вигнера.

Суть транзакционной интерпретации я не смог понять по доступным источникам. Везде слова, картинки и ни одной формулы.

[B3LYP]

warlock66613 в сообщении #1709970 писал(а):

Если на пальцах, то в рамках TSVF всё трактуется так же, как в ММИ, только есть вторая волновая функция, которая маркирует определённый "мир", а точнее "ветвь" как существующую. Поэтому кот всё время жив (либо мёртв) и друг Вигнера тоже не находится в суперпозиции, а находится в определённом состоянии. Если не на пальцах, то надо для начала разобраться с тем как в TSVF трактуется измерение -- я приводил подробные выкладки на форуме, а тогда всё станет ясно и с другом Вигнера.

Можно ссылки на ваши сообщения с этими выкладками?
Могу предположить, что эксперимент ЭВ с бомбами в TSVF трактуется так же, как в ММИ: бомба взрывается в альтернативной вселенной, а мы в нашей вселенной получаем информацию о том, что бомба в той вселенной взорвалась, причём у нас та же бомба, только у нас она не взорвалась. Только в TSVF мы ещё говорим что какая-то вторая волновая функция маркирует, что наша вселенная существует, а та нет? Тогда надо разъяснить понятие "существует". Речь об амплитуде волновой функции, или чём-то другом? Можно ли назвать ту вселенную, где взорвалась бомба, "сном"?

[warlock66613]

B3LYP в сообщении #1710381 писал(а):

Могу предположить, что эксперимент ЭВ с бомбами в TSVF трактуется так же, как в ММИ: бомба взрывается в альтернативной вселенной, а мы в нашей вселенной получаем информацию о том, что бомба в той вселенной взорвалась, причём у нас та же бомба, только у нас она не взорвалась.

Нет, так нельзя. Я и для ММИ не уверен, что это сколь-нибудь корректное описание. Нет в ММИ передачи информации между альтернативными вселенными. В TSVF альтернативных вселенных попросту нет, так что тем более информации неоткуда передаваться.

B3LYP в сообщении #1710381 писал(а):

Можно ссылки на ваши сообщения с этими выкладками?

https://dxdy.ru/post1568641.html#p1568641

[B3LYP]

warlock66613
Можно ещё чуть разъяснений. Как я понял, в эксперименте с котом Шредингера, так же будут две вселенные - в первой кот жив во второй мёртв - но одна из этих вселенной будет "существующей", а вторая "не существующей"?
Можно ли провести аналогию между этой "степенью существования" вселенной и тем фактом, что мнимые числа "существуют в меньшей степени", чем действительные?
А может эта "степень существования" это просто амплитуда волновой функции? Но как тогда это сочетать с правилом Борна?
Как определить эту "степень существования" вселенных с котами из каких-то знаний о будущем?
И ещё вопрос: может быть ММИ - это частный случай интерпретации TSVF?

[B3LYP]

warlock66613

Можете назвать литературу, видео, чтобы я попытался сам почитать и найти ответы на мои вопросы?

[warlock66613]

B3LYP в сообщении #1711386 писал(а):

в эксперименте с котом Шредингера, так же будут две вселенные - в первой кот жив во второй мёртв - но одна из этих вселенной будет "существующей", а вторая "не существующей"?

TSVF имеет две альтернативные, равноправные формулировки.

Первая содержит две волновых функции, одну обычную, другая же обычно задаётся в далёком будущем и включает в себя результаты всех проделанных измерений, а затем эволюционирует из будущего в прошлое.

Вторая формулировка объединяет две волновых функции в единый объект -- матрицу плотности.

Соответствующая интерпретация постулирует, что именно матрица плотности из второй формулировки представляет собой онтологию, существующее, Вселенную. Но расчёты удобнее производить в первой формулировке, с двумя волновыми функциями. При этом первая волновая функция -- это в точности волновая функция ММИ, ветвящаяся на миры. Но в то время как в ММИ эта волновая функция и есть онтология, и значит все эти миры существуют, в TSVF это просто математический артефакт, результат неоконченного расчёта. Влияние второй функции и сводится к тому, что из всех миров первой волновой функции отбирается только один, а остальные не дают вклада в результирующую матрицу плотности.

В эксперименте Шрёдингера в матрице плотности будет только один мир, одна вселенная, а в волновой функции будут два мира.

B3LYP в сообщении #1711386 писал(а):

тем фактом, что мнимые числа "существуют в меньшей степени", чем действительные

Такой "факт" мне не известен.

B3LYP в сообщении #1711386 писал(а):

Как определить эту "степень существования" вселенных с котами из каких-то знаний о будущем?

Это не степень, это бинарная характеристика -- либо существует, либо нет. Определяется по тому, дал ли мир ненулевой вклад в матрицу плотности. Оказывается, что вклад даёт всегда один мир -- это я и демонстрировал в вычислении на которое давал ссылку.

B3LYP в сообщении #1711386 писал(а):

может быть ММИ - это частный случай интерпретации TSVF?

Нет, у них разная онтология: волновая функция в ММИ, матрица плотности в TSVF.

B3LYP в сообщении #1711962 писал(а):

Можете назвать литературу, видео, чтобы я попытался сам почитать и найти ответы на мои вопросы?

По TSVF мало литературы. Вся база есть в статье The Two-State Vector Formalism of Qauntum Mechanics: an Updated Review.

[B3LYP]

warlock66613

Начал читать статью Агаронова, и возникли первые вопросы:
1) Он пишет

Цитата:

In the standard quantum mechanics, a system at a given time t is described
completely by a quantum state
|Ψi, (1)
defined by the results of measurements performed on the system in the past
relative to the time t.

Почему именно в прошлом? Я пока не очень понял суть, что в понимании отцов-основателей квантовой механики есть измерение. В эксперименте с котом Шредингера, мы измеряем состояние радиоактивной частицы; и там ведь вроде сначала эта частица имеет какое-то состояние (распалась или не распалась), и уже потом мы это измеряем так сказать с помощью кота. Не так?

2)
Заодно задам вопрос по квантовой химии. Предположим, мы посчитали молекулу бензола и получили волновую функцию:



Правильно ли я понял, что это подразумевает решение время-независимого УШ, а времязависимое выглядит так что мы эту волновую функцию из картинки умножаем на $Ae^{-ikt}$?

3) И вернусь к вопросу о времени измерения: предположим мы у этой молекулы экспериментально померили квадрупольный момент, разве это не выглядит так что "сначала есть волновая функция по картинке, потом мы по этой ВФ делаем измерение"?

4) Далее Агаронов пишет

Цитата:

It might be that the system at time t is not described
by a pure quantum state, but by a mixed state (density matrix). However, we
can always assume that there is a composite system including this system which
is in a pure state.

Я думал что любую систему в смешанном состоянии можно разбить на несколько подсистем, каждая из которых находится в чистом состоянии? Или не так?

5) Далее он пишет:

Цитата:

The concept of a quantum state is time-asymmetric: it is defined by the
results of measurements in the past. This fact by itself is not enough for the
asymmetry: in classical physics, the state of a system at time t defined by the results of the complete set of measurements in the past is not different from the state defined by the complete measurements in the future. This is because for
a classical system the results of measurements in the future are defined by the
results of measurements in the past (and vice versa). In quantum mechanics this
is not so: the results of measurements in the future are only partially constrained
by the results of measurements in the past. Thus, the concept of a quantum
state is genuinely time-asymmetric.

Снова не понятно: почему собственно в КМ измерение асимметрично, а в ньютоновской симметрично? Можно ли сослаться на ваши слова, что когда открыли квантовую механику, её отцы что-то странное намудрили и мы до сих пор это расхлёбываем?

6) И вопрос по вашему предыдущему посту. Вы сказали, что "степень существования" вселенной в TSVF это бинарная характеристика; но ведь в ММИ "степень существования" это амплитуда, тогда может в TSVF есть сразу две разные "степени существования"?

[realeugene]

B3LYP в сообщении #1712658 писал(а):

Правильно ли я понял, что это подразумевает решение время-независимого УШ, а времязависимое выглядит так что мы эту волновую функцию из картинки умножаем на $Ae^{-ikt}$?

Нет, и если это не опечатка, то вам совершенно трчно слишком рано залазить в интерпретации КМ

[warlock66613]

B3LYP в сообщении #1712658 писал(а):

Начал читать статью Агаронова

По-русски он обычно Ааронов.

B3LYP в сообщении #1712658 писал(а):

Почему именно в прошлом?

Потому что так обычно описывается "жизненный цикл" квантомеханических систем в нерелятивистской квантовой теории с проективными измерениями: есть система в некотором состоянии $\Psi$, оно эволюционирует в соответствии с уравнением Шрёдингера, затем её измеряют в каком-то базисе, в результате чего в соответствии с проекционным постулатом она переходит в другое состояние, полностью определяемое результатом измерения, потом она снова эволюционирует, затем её снова измеряют и т. д. Поскольку шрёдингеровская эволюция унитарна, можно сказать, что волновая функция в любой момент времени определена последним измерением, которое было в прошлом относительно этого момента времени.

B3LYP в сообщении #1712658 писал(а):

Правильно ли я понял, что это подразумевает решение время-независимого УШ

Насколько я знаю да, в квантовой химии (и не только) нас обычно интересуют стационарные состояния, а их можно найти решив "время-независимое УШ" (которое на самом деле является уравнением на собственные состояния гамильтониана).

B3LYP в сообщении #1712658 писал(а):

времязависимое выглядит так что мы эту волновую функцию из картинки умножаем на $Ae^{-ikt}$?

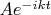
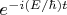
На $e^{-i(E/\hbar)t}$. И потом берём произвольную нормированную линейную комбинацию таких решений. А что такое у вас тут $A$?

B3LYP в сообщении #1712658 писал(а):

предположим мы у этой молекулы экспериментально померили квадрупольный момент, разве это не выглядит так что "сначала есть волновая функция по картинке, потом мы по этой ВФ делаем измерение"?

Волновая функция есть и до и после измерения. Возможные результаты измерения и их вероятности определяются волновой функцией до измерения, а волновая функция после измерения определяется результатом измерения.

B3LYP в сообщении #1712658 писал(а):

Я думал что любую систему в смешанном состоянии можно разбить на несколько подсистем, каждая из которых находится в чистом состоянии?

А почему вы думали такую ерунду? Системе в смешанном состоянии можно сопоставить (вообще говоря, неоднозначно) воображаемый взвешенный ансамбль идентичных систем, находящихся в чистых состояниях. Это не имеет никакого отношения к разбиению на подсистемы и ансамбль этот чисто условный, воображаемый. В смешанном состоянии может быть и кубит, который на подсистемы не разбить никак -- нет у него подсистем.

B3LYP в сообщении #1712658 писал(а):

почему собственно в КМ измерение асимметрично, а в ньютоновской симметрично?

Потому что ньютоновская механика в принципе симметрична, а в квантовой механике -- по крайней мере как она обычно даётся в учебниках -- есть проекционный постулат, который явно эту симметрию нарушает.

B3LYP в сообщении #1712658 писал(а):

Можно ли сослаться на ваши слова, что когда открыли квантовую механику, её отцы что-то странное намудрили и мы до сих пор это расхлёбываем?

А где я такое сказал? Самое похожее что я могу припомнить из того что я говорил, это то, что в процессе создания квантовой механики пришлось отказаться от реализма и хотя это очень хорошо сработало в тот момент времени, стратегически, из сегодняшнего дня, это выглядит ошибкой.

B3LYP в сообщении #1712658 писал(а):

но ведь в ММИ "степень существования" это амплитуда

В одной из трактовок ММИ и не в самой популярной я бы сказал.

B3LYP в сообщении #1712658 писал(а):

тогда может в TSVF есть сразу две разные "степени существования"?

Нету там степеней. Есть матрица плотности и она является моделью существующего без всяких степеней.