утверждается, что понятие «потенциальная бесконечность» устарело и сейчас не принято в математике
Ну да, устарело. Ничего полезного по его мотивам не придумали.
А как же тогда быть с методом математической индукции? Этот метод позволяет в математике строго и корректно рассуждать о бесконечных процессах и бесконечных множествах, оставаясь в рамках конечных доказательств. Как раз та самая потенциальная бесконечность. Хотя в ZFC метод математической индукции выводится из аксиом бесконечности и фундирования, но ведь ZFC не является единственно возможным подходом развития понятия множества (см. ниже).
Ну, примерно так.
А давайте примерно так:
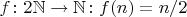
(нумеруем четные числа)
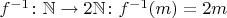
(восстанавливаем четное число по номеру).
Это взаимно-однозначное соответствие или мех собачий?
С этим я согласен. Речь о другом. Скажите, кто нам запрещает строить множества

и

не как актуальные множества, а как ряды с возможным продолжением? Ну, например, так:
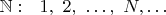

Для этих рядов можно установить ВОС, однако видно, что на любом конечном отрезке (даже если он заканчивается числом гуголплекс в степени гуголплекс) множество

не может быть подмножеством множества

, так как содержит числа, не содержащиеся в

. Например,

. Эту невозможность для данных рядов можно и методом математической индукции доказать.
Множество называется бесконечным, если оно содержит любое наперед взятое число элементов. Множество называется бесконечным по Дедекинду, если оно равномощно собственному подмножеству. То, что эти два понятия эквивалентны - это теорема, которая доказывается в ZFC, причем существенно используется аксиома выбора. Без аксиомы выбора этого доказать нельзя.
Все прекрасно. Но помимо ZFC придумано много других вариантов теории множеств: NBG, Морса - Келли, Крипке –Платека, Тарского – Гротендика и
это еще не все. В этом плане понятию множества повезло. А, может быть, наоборот, не повезло, и мы в итоге перестали понимать, что это такое?
Почему бы на фоне этого многоголосья не предложить простую и понятную для школьников и технарей теорию множеств на основе [url=https://ru.wikipedia.org/wiki/Алгебра_множеств_(по_Куранту_и_Роббинсу)]алгебры множеств[/url], которая была предложена Курантом и Роббинсом? Можно даже выразить ее как аксиоматическую систему, наподобие той, которая была
предложена Булосом для конечных множеств. А чтобы работать с бесконечностью, можно дополнить полученную систему принципом математической индукции.
И, тем не менее, это правило (обобщения)без всяких ограничений присутствует в большинстве известных руководств по математической логике.
Значит те руководства, которые Вы читали, забыли сказать про эти ограничения. А они есть.
Ой, что-то не верится, что забыли!