Меня потрясло то, что для задачи «выполнимость КНФ» установлено взаимно однозначное соответствие с десятками тысяч задач из разных областей математики (
монография Гэри и Джонсона).
Также меня потрясло то, что в математике происходит поиск (порой успешный) весьма сложных соотношений и закономерностей, но при этом не замечаются грубые нарушения элементарной логики. Приведу два примера.
1. Правило обобщения в исчислении предикатов: из формулы

выводится
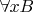
.
Более абсурдного соотношения, которое опровергается
простыми примерами, трудно придумать. И, тем не менее, это правило без всяких ограничений присутствует в большинстве известных руководств по математической логике.
2. Считается бесспорным, что для бесконечного множества можно установить взаимно однозначное соответствие (ВОО) между ним и его строгим подмножеством.
Классический пример такого ВОО --- между натуральным рядом и содержащимся в нем рядом четных чисел.
Пусть начало натурального ряда содержит числа от 1 до
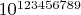
. Число его членов больше количества атомов в наблюдаемой части Вселенной примерно в
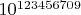
раз. А число четных чисел в нем равно числу
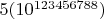
т.~е. ровно половине этого количества. Методом математической индукции можно доказать, что
при неограниченном продолжении ряда между множеством чисел натурального ряда и множеством содержащихся в нем четных чисел ВОО установить невозможно. И, тем не менее, принятое ВОО для бесконечных множеств считается безусловной истиной, а любые попытки его опровергнуть встречаются в штыки. А чтобы устранить возможность такого вмешательства в святая святых в будущем, утверждается, что понятие «потенциальная бесконечность» устарело и сейчас не принято в математике.