Значит концентрация выше а значит и энергетически он выше базы
Это бессмысленная фраза; слова "он выше базы" не имеют смысла. В каждой из трёх областей (в эмиттере, в базе и в коллекторе) на энергетической диаграмме по вертикали располагаются значения одноэлектронной энергии и среди них важные для нашего понимания уровни энергии. А именно:
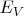
-- это потолок валентной зоны. Ниже этого уровня лежат тесно прижавшись друг к другу уровни энергии (т.е. лежит широкая вдоль вертикали полоса энергии), которые в большинстве своём заселены электронами. Малая доля этой энергетической полосы, вблизи потолка, свободна от электронов, и про эти не занятые электронами уровни мы говорим, что они заселены "дырками". В ФТТ доказывается, что дырки в валентной зоне ведут себя как подвижные носители положительного заряда (в отличие от электронов - носителей отрицательного заряда).
Насколько мало или много этих дырок - это зависит от наличия легирующих примесей и их типа в рассматриваемой области полупроводника. Если есть немало донорных примесей (область n-типа), то можно считать, что дырок почти нет, т.е. валентная зона заселена электронами почти до потолка, до уровня энергии
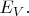
Дырок очень мало. Если, наоборот, есть немало акцепторных примесей (область p-типа), то дырки присутствуют в заметном количестве.
Почему так - это надо объяснять с квантовой механикой и с формулами. Там речь идёт о том, что состояния носителей заряда в зонах проводимости и в валентной "делокализованные", подвижные, а на примесных центрах состояния "локализованные", связанные. На энергетической диаграмме примесные состояния можно показывать как акцепторные уровни энергии

и как донорные уровни энергии
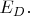
Пока не будем в это вдаваться.
Если примесей нет (на практике это означает, что в реальном кристалле примеси и другие дефекты кристаллической решётки всегда есть, но тут заговорили о случае, когда их пренебрежимо мало), то и дырок очень мало в валентной зоне, и электронов очень мало в зоне проводимости. Такой полупроводник называют "собственным".
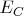
-- это дно зоны проводимости. Выше лежит полоса энергии (сама зона проводимости), которая в большинстве своём свободна от электронов. Но небольшая доля состояний зоны проводимости, вблизи дна, заселена электронами. Таких электронов мало в области p-типа , и заметно больше в области n-типа.
Интервал энергии шириной
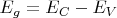
между потолком валентной зоны и дном зоны проводимости называется запрещённой зоной. В нём нет подвижных (делокализованных) состояний носителей заряда. В нём располагаются примесные уровни, но мы решили их пока не рисовать.

- значение энергии, называемое в технике "уровнем Ферми" (хотя более строго в физике оно называется химическим потенциалом и часто обозначется буквой

или

а понятие "уровень Ферми" в физике может от химпотенциала отличаться. Но в этот нюанс тоже не будем пока вдаваться, будем пользоваться техническим жаргоном).
Величина

не имеет вот прям-таки наглядного смысла, а просто служит параметром в функции распределения Ферми-Дирака

, которая зависит ещё и от абсолютной температуры

и количественно описывает возможную заселённость электронами состояний с энергией

если бы все такие состояния существовали.
Конкретно: при
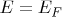
обязательно получается
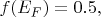
и это означает вот что:
Если состояние с энергией
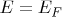
доступно электрону (т.е. это примесный уровень, или это состояние в зоне валентной, или в зоне проводимости), то оно с вероятностью

заселено электроном и с такой же вероятностью свободно от электрона. Т.е. из-за хаотического теплового движения электроны всё время то приходят на этот уровень, то уходят с него.
А состояния с энергией

большей уровня

заселены с меньшей вероятностью, чем

И чем выше

тем меньше там заселённость электронами. Это "хвост" функции распределения, тянущийся по шкале энергии вверх. И он ещё от температуры сильно зависит: чем сильнее нагреть кристалл, тем сильнее этот хвост растягивается вверх на энергетической диаграмме, т.е. увеличивается вероятность обнаружить электрон (в разрешённом состоянии) с данной энергией

большей уровня Ферми; хотя эта вероятность всегда остаётся меньше

И наоборот: состояния с энергией

меньшей уровня

(если они разрешённые для электрона, т.е.

не лежит тупо в запрещённой зоне, где вообще никаких электронных состояний нет) заселены с большей вероятностью, чем

И чем ниже под уровнем Ферми на диаграмме значение

тем больше там заселённость электронами. А с повышением температуры эта заселённость уменьшается. В валентной зоне это означает, что там при нагревании появляется больше дырок.
Наконец, ещё один очень важный факт: при термодинамическом
равновесии (т.е. когда микроскопическое хаотическое тепловое движение электронов есть, но нет макроскопического тока) уровень Ферми постоянен вдоль полупроводника, даже если в разных областях полупроводника есть разного типа примеси. Т.е. на энергетической диаграмме с контачащими друг с другом областями n-типа и p-типа уровень

должен изображаться одной и той же горизонтальной линией во всех областях.
На вашей диаграмме видны три разных уровня Ферми. Это более сложный случай, неравновесный. Нарисуйте, пожалуйста, новую диаграмму аналогично, но для равновесного случая. Сначала надо будет с ней аккуратно разобраться, если будут вопросы. А тогда уже легко будет разобрать, что получается, когда к переходам прикладывают разность потенциалов и течёт ток.
Для простоты мы рассматриваем p- и n-области в одном и том же легированном кристалле, т.е. это не соединение разных химических веществ, не гетероструктура. Поэтому при рисовании
равновесной диаграммы надо исходить из того, что:
1. Во всех областях ширина зазора между потолком валентной зоны и дном зоны проводимости, т.е. запрещённая зона

должна быть одинаковой.
2. Уровень Ферми

один и тот же во всех областях ; изображается ровной горизонтальной линией.
3. И при этом в разных областях уровень Ферми должен быть по-разному расположен относительно потолка валентной зоны и зоны проводимости - в строгом соответствии со сказанным выше о смысле

как о параметре, связанном с заселённостью электронами уровней энергии в зонах.