warlock66613В этом месте
Тогда вероятность обнаружить систему в состоянии

по правилу Борна

есть
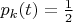
, причём этот вывод справедлив для любого из двух возможных чистых начальных состояний системы — как для
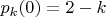
, так и для
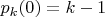
потерян важный для практики эффект - "квантовые биения". Потому что Вы рассмотрели два разных варианта постановки опыта, а ещё два почему-то пропустили, и в одном из пропущенных вариантов квантовые биения как раз и есть. Понятно, что Вы стремились написать всё кратко.
Писать подробно - да это нудно, долго, но иначе так и останется барандесовская путаница. Поэтому не ленюсь и пишу подробно, как полагается по квантовой механике:
Раз гамильтониан

задан в виде матрицы

значит есть два базисных вектора состояний:

и
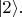
Как и Вы, нумерую их индексом
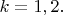
Это не стационарные состояния, т.е. не состояния с определённой энергией, так как гамильтониан в этом базисе не диагонален. Назову их условно состояниями с определённым "положением" - они собственные для некоего оператора положения
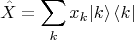
Решив задачу на собственные значения гамильтониана,
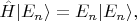
получаем два уровня энергии:
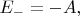
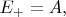
и принадлежащие им два стационарных состояния (определённые с точностью до фазовых множителей, несущественных в этой записи):
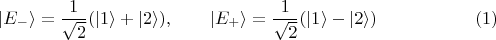
Общее решение

нестационарного уравнения Шрёдингера имеет вид суперпозиции стационарных состояний. Если для произвольного момента времени

коэффициенты суперпозиции задать численно их модулями
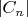
и фазами
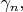
то в произвольный момент времени

имеем
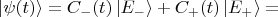
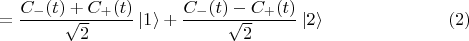
где
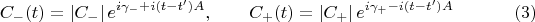

В наш (Ваш) гамильтониан измерительные приборы не входят, поэтому

описывает эволюцию кубита между моментами времени

и

без измерений - без вмешательства приборов. Если коэффициенты в

заданы для момента времени

то этот момент следует считать начальным в данной эволюции, т.е.

так как начальные условия в физике обычно задаются для прошлого, а не для будущего рассматриваемой системы. В квантовой механике системы с динамикой, описываемой гамильтонианом без вмешательства приборов, нет нескольких начальных условий (типа при

а потом ещё и при
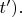
Просто

при

описывает начальное состояние, приготовленное тем или иным измерением в ранний момент времени

и та же самая зависимость от времени

описывает результат эволюции к произвольному моменту

в который можно произвести любое измерение.
У нас в рассмотрении присутствуют два базиса - базис с определёнными энергиями

где
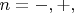
и базис с определёнными положениями

где
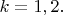
Поэтому можем для любого момента
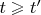
рассмотреть два варианта измерений и выписать по правилу Борна соответствующие выражения вероятностей:
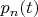
- для обнаружения системы с определённой энергией, либо:

- для обнаружения системы в определённом положении. Из верхней строчки в

получаем:
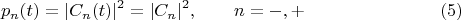
Из нижней строчки в

с учётом

получаем:
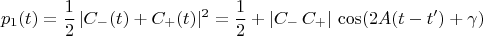
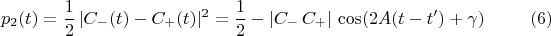
где

Варианты опытов:
1) Начальное состояние приготавливается (проекционным измерением) как состояние с определённой энергией, и затем производится измерение тоже энергии. Тогда, согласно

имеем
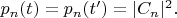
Например, если было приготовлено состояние с энергией

т.е.
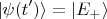
то
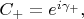
так что:
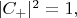
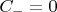
(учли нормировку
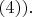
Т.е. стационарное состояние в ходе эволюции без внешнего вмешательства в систему остаётся стационарным.
2) Начальное состояние приготавливается как состояние с определённой энергией, и затем измеряется положение. Тогда имеем формально
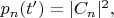
а конечные вероятности

вычисляются из формул

Например, если было приготовлено состояние с энергией

т.е.
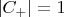
и
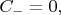
то
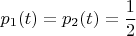
Этот вариант Вами рассмотрен.
3) Начальное состояние приготавливается как состояние с определённым положением и затем измеряется энергия. Тогда
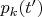
выписываем по формулам (6) при

задав должным образом

а конечные вероятности есть
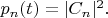
Например, если
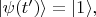
то
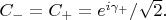
Если
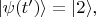
то
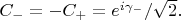
В обоих случаях
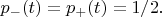
Этот вариант Вами рассмотрен.
4) Начальное и конечное состояния это состояния с определённым положением. Например, если
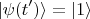
то
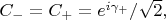
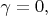
так что
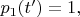
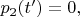
а для конечных вероятностей получаем выражения:
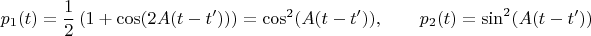
Это квантовые биения: система в ходе эволюции периодически переходит из одного состояния в другое.
Не вижу здесь никакого способа ввести
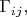
кроме уже упоминавшегося тривиального:
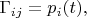
где

вычисляется по правилам квантовой механики. Индекс

это либо

либо

либо номер ещё каких-то других базисных состояний, если рассматриваются измерения ещё и других физических величин. Как видим,

зависит от выбора измеряемой величины, хотя модель эволюционирующей системы одна и та же. Поэтому не может быть универсальной
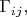
т.е. зависящей только от модели системы без измерительных приборов; а включить описание макроскопических приборов в пригодный для
реальных расчётов гамильтониан невозможно. И, как видим это не нужно; все практические применения квантовой теории в физике прекрасно обходятся без наблюдателей с их приборами в гамильтонианах. И в классической механике тоже так дело обстоит.