Интерпретации квантовой механики

[realeugene]

warlock66613 в сообщении #1696137 писал(а):

Обобщённый стохастический процесс, который, как оказывается, эквивалентен квантовой механике — это просто $p_i(t) = \Gamma_{ij}(t) p_j(0)$

Всё линейно? Как коллапс происходит?

[warlock66613]

realeugene в сообщении #1696156 писал(а):

Всё линейно? Как коллапс происходит?

Линейность тут только та, что требуется базовыми принципами теории вероятностей.

Если есть точка делимости процесса, то есть момент $t'$ такой, что $\Gamma(t \leftarrow 0) \equiv \Gamma(t \leftarrow t') \Gamma(t' \leftarrow 0)$, то наблюдатель, знающий состояние системы в момент $t'$, будет описывать систему иначе, чем знающий только состояние в момент $0$. Именно, первый наблюдатель будет описывать систему с помощью вектора состояния, который по отношению в вектору состояния второго, будет "сколлапсировавшим". У первого наблюдателя вектор состояния будет $U(t \leftarrow t') e_j$, если система оказалась в состоянии $j$ в момент $t'$, в то время как для второго наблюдателя вектор состояния будет $U(t \leftarrow t') U(t' \leftarrow 0) e_i$, где $i$ — состояние в момент 0.

[realeugene]

warlock66613 в сообщении #1696161 писал(а):

то наблюдатель, знающий состояние системы в момент $t'$, будет описывать систему иначе, чем знающий только состояние в момент $0$.

Это та же ММИ с другой математикой?

[warlock66613]

realeugene в сообщении #1696163 писал(а):

Это та же ММИ с другой математикой?

Нет, вообще ничего общего. Нет многих миров, нет онтологической волновой функции, зато есть выделенный (онтологический) базис, а любая неопределённость (в онтологическом базисе) исключительно следствие чьего-то незнания. В ММИ электрон для создания интерференционной картины пролетает через обе щели, тут совсем не обязательно: потенциальной и не реализовавшейся возможности пролететь через вторую щель уже достаточно для появления интерференционной картины.

-- 02.08.2025, 20:32 --

chislo_avogadro в сообщении #1696154 писал(а):

нужно ли здесь вообще какое-либо доказательство, достаточно ведь вспомнить о двухщелевом эксперименте, где каждая пролетающая частица интерферирует

Это слова, за которыми не видно формул. Ну интерферирует, и что? Как из этого следует невозможность описывать одно и то же онтологическое состояние разными волновыми функциями в зависимости от ансамбля?

chislo_avogadro в сообщении #1696154 писал(а):

Ещё наглядней, если взять интерферометр Маха-Цандера с настройкой на попадание выходящей частицы лишь на один детектор. Там ведь никаких ансмблевых свойств не видно, поскольку каждая отдельная частица попадает только в этот детектор.

Это и есть ансамблевое свойство: ансамбль таков, что каждая частица попадает в определённый детектор.

[realeugene]

warlock66613 в сообщении #1696170 писал(а):

Нет, вообще ничего общего. Нет многих миров, нет онтологической волновой функции, зато есть выделенный (онтологический) базис, а любая неопределённость (в онтологическом базисе) исключительно следствие чьего-то незнания. В ММИ электрон для создания интерференционной картины пролетает через обе щели, тут совсем не обязательно: потенциальной и не реализовавшейся возможности пролететь через вторую щель уже достаточно для появления интерференционной картины.

Выглядит как просто другими словами (распределение вероятностей состояний в конфигурационном пространстве) обозвали универсальную волновую функцию. А функция перехода - это гамильтониан. Или его экспонента если промежуток времени конечный. Точнее, нет, если наблюдатель знает вероятность в некоторый момент времени, это эквивалентно относительной волновой функции наблюдателя. При этом, как я понимаю, тут наблюдатель - какой-то чисто классический объект и сам не описывается вероятностно?

[warlock66613]

Дело не в том, как что обозвали. Дело в том, что онтология совершенно иная. То есть это онтологически различные теории.

Принципиального отличия между квантовыми и классическими объектами в теории нет, поскольку квантовые объекты тут тоже вполне себе классические. Так что нельзя и сказать "чисто классический" объект наблюдатель или не "чисто". Это просто объект, такой же как и все другие объекты.

[yesterday]

warlock66613
Мне будет интересно.

[realeugene]

warlock66613 в сообщении #1696184 писал(а):

Дело не в том, как что обозвали. Дело в том, что онтология совершенно иная. То есть это онтологически различные теории.

Фантазии авторов на тему, что "есть на самом деле", которые невозможно проверить экспериментально в принципе, как-то не особо интересны. Насколько я понимаю, авторы придумали альтернативное математическое описание квантовой системы, эквивалентное стандартному. Эта эквивалентность обосновывает применимость этой математики для описания физической системы, но, с другой стороны, она должна делать эту интерпретацию экспериментально неотличимой от копенгагенской. Но в этом математическом описании нет линейности пространства состояний над полем комплексных чисел? Во что в этой математике превращается главный постулат квантовой механики?

[warlock66613]

realeugene в сообщении #1696205 писал(а):

Но в этом математическом описании нет линейности пространства состояний над полем комплексных чисел?

Нет. Это описание на кинематическом уровне — классическая система, для которой задано пространство состояний без какой-либо структуры вроде векторного пространства.

realeugene в сообщении #1696205 писал(а):

во что в этой математике превращается главный постулат квантовой механики?

В линейность по эпистемологическому начальному состоянию. То есть если мы (применители теории) не знаем начальное состояние в точности, но можем постулировать по тем или иным причинам какое-то распределение вероятностей по начальному состоянию, то вероятности конечных состояний будут линейно зависеть от вероятностей начальных.

[realeugene]

warlock66613 в сообщении #1696209 писал(а):

В линейность по эпистемологическому начальному состоянию.

Но линейность над полем действительных чисел и над полем комплексных - это разные вещи.

warlock66613 в сообщении #1696209 писал(а):

То есть если мы (применители теории) не знаем начальное состояние в точности

А что при этом есть состояние свободной квантовой частицы? Как появляются соотношения неопределённости? У классических частиц вероятностные распределения по импульсам и координатам независимы.

[warlock66613]

realeugene в сообщении #1696226 писал(а):

Но линейность над полем действительных чисел и над полем комплексных - это разные вещи.

Оказывается, в некоторых ситуациях это одно и то же. Линейность вероятностей над полем действительных чисел влечёт линейность амплитуд на полем комплексных.

realeugene в сообщении #1696226 писал(а):

А что при этом есть состояние свободной квантовой частицы?

Строго говоря, это неизвестно. Но если не принимать в расчёт КТП, это могло бы быть просто её положение в пространстве. Именно положение, без скорости. Тогда измерение положения давало бы реальное положение частицы, а вот измерение скорости давало бы величину, возникающую только в процессе взаимодействия с прибором. Соотношение неопределённостей — это соотношение между среднеквадратичными отклонениями этих двух измеримых величин.

[Cos(x-pi/2)]

Уважаемый warlock66613 так похвалил этого парнишку Барандеса, что я даже прочитал его статью (хотя обычно такие статьи подробно не читаю) arXiv:2302.10778. Спорить с warlock66613 не стану, каждый человек имеет право на своё мнение (и моё впечатление от этой статьи Барандеса наверняка тоже не бесспорное).

(Критикую написанное Барандесом)

В вводной части (где он расписывает достоинства своего подхода, ещё не изложив его толком) он пишет, что в его подходе "система стохастически движется по физической траектории в простом, классически выглядящем конфигурационном пространстве. Понятия, связанные с гильбертовым пространством, включая волновую функцию, подобны светоносному эфиру электромагнетизма 19 века, - они больше не являются первичными или онтологическими особенностями теории".

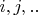
Переходя к конкретике, он пишет: "Формализм для неделимого стохастического процесса проще всего выразить в случае, когда конфигурационное пространство системы имеет конечное число конфигураций". Тогда конфигурации нумеруются индексами $i,j,..$ принимающими дискретные значения $1,2,...,N.$ Хорошо, пусть так. Подобный педагогический приём известен, он удобен и при изложении квантовой механики, - рассматривать систему с конечномерным пространством состояний.

Однако у меня сразу возникает вопрос: не пространство ли состояний квантовой системы автор называет "классически выглядящим конфигурационным пространством"? 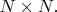Похоже, что какая-то такая путаница имеет место, потому что дальше своё понятие конфигурационного пространства автор никак не разъясняет, но зато вводит $N$-компонентные векторы "конфигурационного базиса" и соответствующие им "конфигурационные проекторы" - матрицы $N\times N.$ И пишет: "с конечной целью воспроизвести обычный формализм квантовой теории в гильбертовом пространстве, в этой статье мы считаем величины $\Theta_{ij}(t)$ 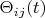комплексными числами". 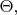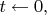Аргумент у этих элементов матрицы $\Theta,$ которая в дальнейшем считается аналогичной унитарному оператору эволюции от $t=0$ до заданного момента времени $t$ в квантовой теории, автор обозначает как $t\leftarrow 0,$ но я для краткости буду писать просто $t.$

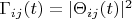
Основные формулы у него такие: $\Gamma_{ij}(t)=|\Theta_{ij}(t)|^2$ есть условная вероятность перехода системы из состояния $j$ в состояние $i,$ и формула для вероятности $p_i(t)$ обнаружить систему в момент $t$ в состоянии $i$

$$p_i(t)=\sum_{j=1}^N \Gamma_{ij}(t)\,p_j(0)\qquad (*)$$

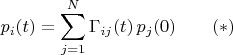
Затем (в разделе 3.2 The Hilbert-space representation) автор переписывает свои формулы и следствия из них в виде, похожем на формализм с матрицей плотности в квантовой теории. Тем самым он пытается убедить читателя в том, что подход автора - основной, а формализм и понятия обычной квантовой теории - вторичные, они, мол, лишь полезный математический инструмент.

С последним я согласен (что квантовая теория это полезный математический инструмент для решения множества задач квантовой физики); известно ведь: "заткнись и вычисляй". И со словами о наличии "неделимых стохастических процессов" согласен - просто ведь квантовая механика описывает эту неделимость и стохастичность более привычными словами: "у частиц нет определённых траекторий"; это принцип неопределённости, с которого начинается изложение в учебниках. Но с попыткой вывода квантовой механики из $(*)$ не согласен; автор перевернул задачу шиворот-навыворот.

Поскольку квантовая механика это хорошо проверенный успешно работающий на практике формализм, а претендующая на эквивалентность с квантовой механикой формула $(*),$ образно говоря, взята автором с потолка, то следует проверить - выводится ли $(*)$ из квантовой теории, а не наоборот. Оказывается, не выводится:

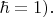
Рассмотрим задачу о динамике волновой функции частицы в статическом потенциале с дискретным энергетическим спектром (одномерное движение для простоты записи, $\hbar=1).$ Вот ответ, т.е. решение волнового уравнения Шрёдингера для волновой функции при $t>0$ с заданной начальной волновой функцией $\psi(x,0):$

$$\psi(x,t)=\sum_{n}c_n\,\psi_n(x)\,e^{-iE_nt}\, \eqno (1)$$

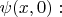
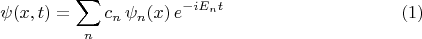
где

$$c_n=\langle \psi_n|\psi(0)\rangle =\int dx\,\psi_n^*(x)\,\psi(x,0)\,\eqno (2)$$

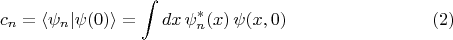
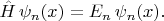
Здесь $\psi_n(x)$ - волновые функции стационарных состояний, решения уравнения $\hat{H}\,\psi_n(x)=E_n\,\psi_n(x).$ Подставим $(2)$ в $(1)$ и обозначим

$$G(x,x';t)=\sum_n e^{-iE_nt}\,\psi_n(x)\,\psi_n^*(x')$$

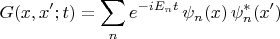
получается:

$$\psi(x,t)=\int dx'\,G(x,x';t)\,\psi(x',0)\,\eqno (3) $$

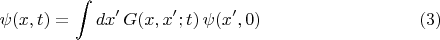
Классическое конфигурационное пространство здесь это числовая ось значений $x.$ Для перехода к дискретным обозначениям Барандеса будем рассматривать значения волновых функций в дискретных точках оси $x$ и запишем, как при численном счёте "методом прямоугольников", интеграл в виде суммы. Чтобы число точек было конечным, можно вести речь о движении частицы в прямоугольной потенциальной яме с бесконечно высокими стенками. Тогда дискретный вариант $(3)$ запишется в виде

$$\psi_i(t)=\sum_j G_{ij}(t)\,\psi_j(0)\,\eqno (4)$$

Распределение вероятностей частицы по точкам конфигурационного пространства даётся квадратом модуля волновой функции (плотность вероятности надо ещё умножать на $dx,$ но этот нюанс важен в реальном численном расчёте, а здесь не принципиален). Возводим модуль выражения $(4)$ в квадрат и обозначаем $p_i(t)=|\psi_i(t)|^2,$ $p_j(0)=|\psi_j(0)|^2:$

$$p_i(t)=\sum_{j'}\sum_j G_{ij'}^*(t)\,G_{ij}(t)\,\psi_{j'}^*(0)\,\psi_j(0) =$$

$$=\sum_j |G_{ij}(t)|^2\,p_j(0) + \sum\sum_{j'\neq j} G_{ij'}^*(t)\,G_{ij}(t)\,\psi_{j'}^*(0)\,\psi_j(0)\,\eqno (5)$$

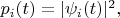
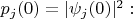
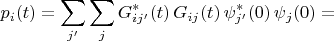
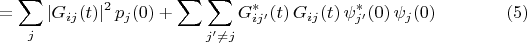
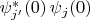
Видно, что не получилась формула $(*),$ Барандес потерял члены, содержащие $\psi_{j'}^*(0)\,\psi_j(0)$ с $j'\neq j.$

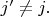
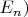
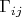
И вообще, похоже, он не хочет признавать, что волновая функция и связанные с ней элементы формализма квантовой механики (оператор Гамильтона, стационарные состояния $\psi_n,$ энергетический спектр $E_n)$ несут намного больше физически важной информации о модели, чем только условные $\Gamma_{ij}$ и безусловные $p_j$ вероятности. Может быть, и классическую механику этот парнишка философ толком не понимает. Как уже правильно подчеркнул realeugene, подобное классическому движение описывается в каждый момент времени не только положением частицы в конфигурационном пространстве, а ещё и импульсом. В "заткнись и вычисляй" квантовой механике главную роль играет принцип суперпозиции: разложением $\psi(x,t)$ по $e^{ipx}$ даётся распределение вероятности дли импульса, разложением по стационарным состояниям даются вероятности $|c_n|^2$ для возможных значений $E_n$ энергии частицы. Взять и объявить весь реально работающий аппарат теории вторичным по отношению к неработоспособной формуле $(*)$ и к сопровождающим её общим словам о неких неделимых стохастических процессах (да ещё и сравнить формализм квантовой механики с представлениями 19-го века об эфире)... это даже не знаю, до какой степени надо не понимать квантовую физику.

О недопонимании Барандесом основ квантовой механики говорит также то, что он лишь мельком упоминает фазовые множители, не анализирует их роль. А ведь в квантовой механике они очень важны для описания динамики. Не удержусь от искушения проиллюстрировать это давнишним своим примером: в этом сообщении вместе с этим сообщением была сформулирована для численного расчёта элементарная задачка о свободном движении волнового пакета на отрезке $0<x<a,$ ограниченном бесконечно высокими потенциальными стенками.

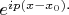
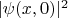
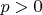
Начальная волновая функция $\psi(x,0)$ частицы задана там как вещественная функция, имеющая колоколообразный график, умноженная на фазовый множитель $e^{ip(x-x_0).$ Хотя начальное распределение вероятности $|\psi(x,0)|^2$ от этого фазового множителя не зависит, именно он и "делает погоду": при $p=0$ пакет стоит на месте, а при $p>0$ бегает от стенки к стенке. Это видно на графиках для $|\psi(x,t)|^2$ (выбор единиц и способ расчёта пояснён в упомянутых сообщениях). Кстати, при отражении от стенки возникает интерференция падающей и отразившейся частей пакета. Т.е. в этом примере интерференционная картина в распределении вероятности для координаты частицы возникает без традиционных "двух щелей":





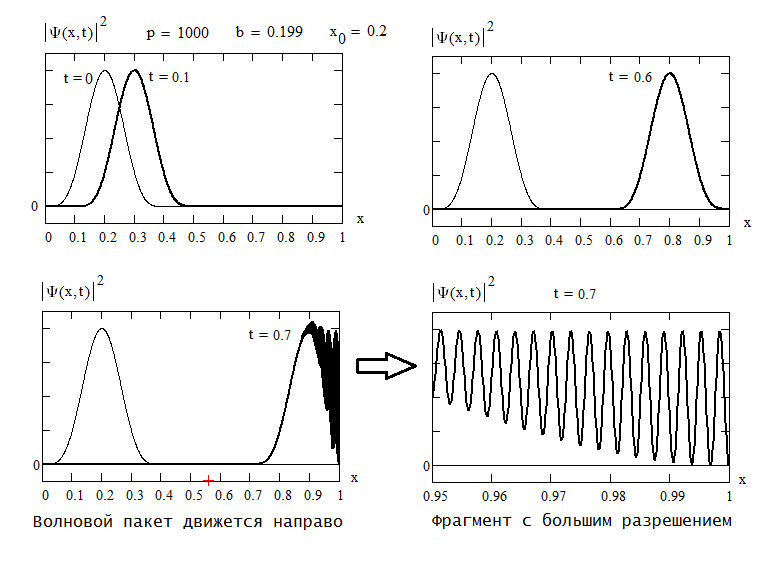
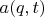
Распределение для импульса (о нём Барандес умалчивает) вычисляется через фурье-коэффициент $a(q,t)$ всё той же волновой функции $\psi(x,t)$ и тоже проявляет динамику:



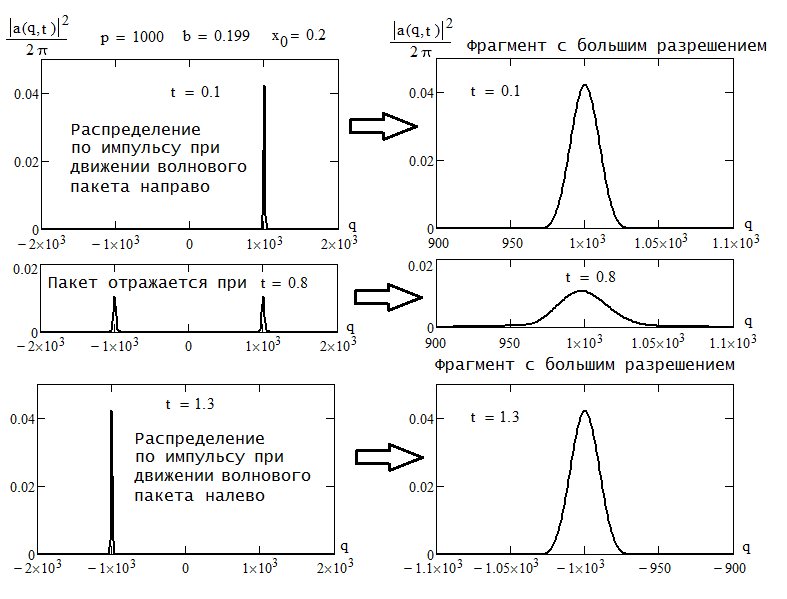
Распределение по энергии (и о нём Барандес ни гу-гу) определяется начальной волновой функцией, оно от времени не зависит:



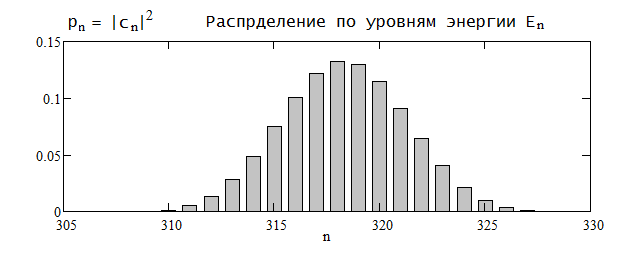
Заодно, вот иллюстрация расплывания волнового пакета - оно становится заметным тем раньше, т.е. на тем меньшем промежутке времени, чем меньшей выбрана начальная ширина $b$ волнового пакета:



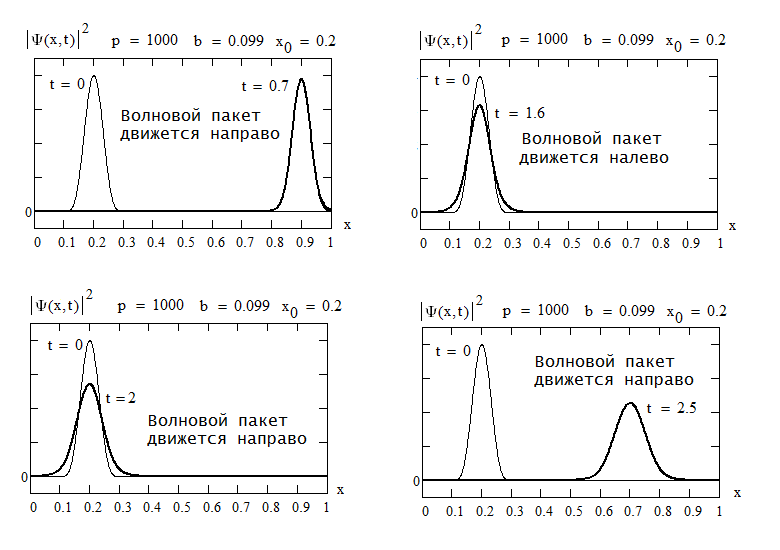
Хотелось бы, чтобы альтернативный подход (а именно так называет своё сочинение Барандес) мог выдавать по крайней мере те же результаты, которые спокойно выдаёт обычная квантовая механика. Но ничего этого у Барандеса нет; есть только слова о неделимом стохастическом процессе и несколько бесполезных для практических расчётов формул. Притом, вот, что он написал в заключительной части статьи о своей точке зрения:

"Эта точка зрения раскрывает некоторые из самых загадочных особенностей квантовой теории. В частности, мы видим, что матрицы плотности, волновые функции и все другие компоненты гильбертовых пространств, хотя и весьма полезны, являются всего лишь математическими дополнениями. Поэтому этим атрибутам не следует придавать прямого физического смысла или относиться к ним так, как будто они непосредственно представляют физические объекты. Они, как и лагранжианы или функции Гамильтона, непосредственно не представляют физические объекты. Суперпозиция - это не буквальное размытие физических объектов, а всего лишь математический артефакт, позволяющий поймать систему в середине неделимого стохастического процесса, представленного с использованием формулировки пространства Гильберта и волновых функций."

С этим можно и поздравить философа Барандеса: похоже, до него дошло то, что давным-давно известно каждому физику-инженеру, т.е. что математический аппарат теории и железо в лаборатории (измерительные установки, приборы, и физические явления в них) - это не одно и то же. А то, что пока ещё неизвестно физикам - какие конкретно стохастические процессы ответственны за квантовые явления, - это остаётся неизвестным и философам. (Поэтому у меня сложилось вот какое мнение о статье Барандеса: это не "бомба", а в плане физики - пустышка, каких напечатано уже море.)

warlock66613, извините пожалуйста, что я влез в Вашу тему с моей доморощенной и многословной критикой Барандеса. Просто душа не вынесла читать его, как мне видится, далёкие от реальной практики эксперимента рассуждения :) Зря я вообще стал его читать (раньше я воздерживался от чтения подобных статей, и постараюсь воздерживаться впредь).

[warlock66613]

Cos(x-pi/2) в сообщении #1696381 писал(а):

Барандес потерял члены, содержащие $\psi_{j'}^*(0)\,\psi_j(0)$ с $j'\neq j.$

Дело в том, что они заведомо равны нулю. Если они не равны нулю, то это просто значит, что нулевой момент времени выбран неверно.

[amon]

warlock66613 в сообщении #1696409 писал(а):

Дело в том, что они заведомо равны нулю. Если они не равны нулю, то это просто значит, что нулевой момент времени выбран неверно.

Формула, приведенная уважаемым Cos(x-pi/2), верна для любого начального момента времени. Ее можно написать так:

$$\psi(x,t)=\int dx'\,G(x,x';t,t')\,\psi(x',t')\,\eqno (3'). $$

Если исходный гамильтониан не зависит от времени, то $G(x,x';t,t')=G(x,x';t-,t'),$ но даже в этом случае надо сохранять перекрестные члены для $p(t).$ Исходную статью не читал, но не одобряю подозреваю, что автор с ошибками переоткрывает тот факт, что уравнение Шредингера совпадает с уравнением Блоха для винеровского стохастического процесса в мнимом времени. То, что время мнимое, убивает интерпретацию $p(t)$ как вероятности.

[warlock66613]

amon в сообщении #1696419 писал(а):

Формула, приведенная уважаемым Cos(x-pi/2), верна для любого начального момента времени.

Это верно, но Барандес предъявляет в нулевому моменту времени особые требования: это не просто произвольный момент времени. Одним из следствий из этих приведённых в статье требований, которые должны удовлетворяться, чтобы момент времени можно было брать за нулевой, как раз и является $\psi_{j'}^*(0)\,\psi_j(0) = 0\quad(j \ne j')$.