Вот типовая кривая с перекосом в активности избирателей

Параметр

пробегает значения от
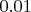
до

с шагом
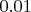 -- 05.07.2020, 14:47 --
-- 05.07.2020, 14:47 --Кроме того, эта модель ничего не говорит про пики на целых значениях.
Это отдельный вопрос.
Ваша модель говорит, какие точки "за-явка" возможны, но не говорит, в каких участках кривой их сколько будет.
А это следующий вопрос.
Действительно, как могут размещаться точки вблизи этой кривой?
1. Наиболее ожидаемый вариант - неким кластером вокруг какой-то одной точки. Он реализуется, когда

примерно одинаков, и имеется некий шум в параметрах модели. Реализацию такого паттерна можно найти в некоторых регионах в картинках Шпилькина.
2. Кластер в какой-то области кривой и некий разреженный хвост от него вдоль кривой. Такое тоже есть в картинках Шпилькина.
3. Несколько кластеров на кривой. Например, два. Очевидно, что в этом случае распределение

будет бимодальным и это нельзя объяснить стечением случайных обстоятельств.
Должен быть какой-то фактор, по которому разделяются кластеры. Для Татарстана, где кластеризация наиболее ярко выражена я его нашел - один кластер это Казань, второй - остальные участки. Вот на каком основании кто-то может утверждать, что доля "За" в Казани и какой-нибудь Елабуге должна быть одинакова?
4. Есть несколько регионов, которые в модель не укладываются. Например, когда точки группируются вдоль
горизонтальной прямой. Это может быть в случае, когда участки по долям протестного и лояльного электората, одинаковы. (как в первом пункте) Но участки сильно разные по доступности. То есть на явку больше влияет не предпочтения избирателей, а доступность голосования.
Такие картинки тоже есть у Шпилькина, но для единичных регионов. Насколько помню, в Крыму или Севастополе так.