Концепция науки и образования в современной России

[kry]

EUgeneUS в сообщении #1184699 писал(а):

Ответ $1/4$, впрочем, как и $4/16$ неверный, при условии, что задача из части В ЕГЭ. А так-то верный, конечно.

Вообще-то, если мне не изменяет память, то подобная задача раньше была в части C.

[Brukvalub]

kry в сообщении #1184750 писал(а):

Вообще-то, если мне не изменяет память, то подобная задача раньше была в части C.

Память вам изменяет. В части С никогда не было задач по теории вероятностей.

[kry]

Brukvalub в сообщении #1184757 писал(а):

Память вам изменяет. В части С никогда не было задач по теории вероятностей.

Значит, я ошибся. Мне казалось, что до разделения на базовый и профильный уровни это было то ли С-5, то ли С-6.

[--mS--]

(Оффтоп)

GAA в сообщении #1184693 писал(а):

Я предполагал, что от школьника в этом задании ожидается использование классического определения вероятности.

Именно с помощью классического определения вероятности задача и решается. Есть $4$ равновозможных исхода. Не хочется $4$ - есть $16$. Тоже равновозможных. Зачем нужны $16!$ исходов? С таким же успехом можно и $16!^2$ рассмотреть (и ещё больше, наверное, можно притянуть).

[Shtorm]

GAA в сообщении #1184693 писал(а):

.....
(Не сочтите за занудство. Причину вопроса указал выше. Развивать свой оффтопик не буду. А то ещё самому себе или админам нужно будет мне предупреждение выписывать.)

Ну, а почему собственно? Тема у нас многовекторная, мы уже много вопросов обсудили. Обсуждение конкретных задач из ЕГЭ может прояснить ситуацию с влиянием ЕГЭ на образование в России. Не сочтите это за попытку обсудить действия модераторов не в том разделе, а сочтите это за попытку обсудить вектор (вектора) дальнейшего развития данной темы.

[GAA]

--mS--, потому что, при моей интерпретации условия, исход случайного эксперимента — это набор 16 чисел (вытянутых капитанами команд). Откуда он берётся? Из попытки интерпретировать фразу условия — «Капитаны команд тянут по одной карточке». Причем я в варианте решения интерпретировал эту фразу как «Капитаны команд тянут по очереди по одной карточке». Т.е. у меня выборка без возвращения. Я мысленно представил барабан с карточками и по очереди подходящих к нему капитанов. Перемешивание в барабане идеальное. $i$-ый по списку капитан может выбрать одну их оставшихся $16-(i-1)$ карточек с одинаковым шансом. Нужно ли знать число этих наборов длиной 16? В данной задаче нет. На некоторой $i$-ой позиции в списке находится капитан команды России. Для решения задачи можно найти распределение карточек на $i$-ой, но можно доказать, что распределение карточек на любой позиции одно и то же. Из последнего будет следовать при естественных предположениях 16 равновозможных исходов. Из них 4 благоприятствуют наступлению искомого события.

Если я сразу беру 16 исходов, то из каких-то соображений должен вывести их равновозможность. Постулирую: существует жеребьёвка, называемая хоть сколько-то разумной, при которой «у всех капитанов одинаковые распределения вытянутых карт». Отсюда при очевидных предположениях получаем хоть 16 равновозможных исходов (с четырьмя благоприятствующими), хоть 4 исхода (с одним благоприятствующим). Остается привести конкретный пример (модель) такой жеребьёвки. Мой вариант выше.

Как я понял из обсуждения, существование хотя бы одной такой жеребьёвки очевидно и не требует предъявления. Или по-другому, существование хоть сколько-то разумной жеребьёвки не менее очевидно, чем существование (идеальной) выборки с возвращением.

Мне естественно понятней вариант конкретной реализации жеребьёвки, но и такой ответ вполне устраивает - очевидно и очевидно. Как это воспринимают школьники я пока не знаю.

[Otta]

GAA
Попробую написать примерно так, как я студентам рассказываю аналогичную задачу - рассказываю я всегда после формулы полной вероятности и когда они уже успели поудивляться одинаковости ответов.

На столе лежит 16 карточек, из них 4 хороших. С какой вероятностью (не важно на каком шаге) нам достанется хорошая?

Все 16 человек пронумерованы, заходят - пусть по очереди- и ставят на выбранной карточке свой номер. Наш номер 1. Карточки лежат изнанкой вверх. В итоге мы имеем 16 карточек, на которых случайным образом (для них) были расставлены 16 чисел. Вероятность того, что 1 написана на хорошей карточке, понятно какая. И видно, что на окончательный результат жеребьевки очередность не влияет.

(Оффтоп)

Все-таки устно лучше рассказывать ))

[dsge]

Из ЛС

Munin писал(а):

dsge в сообщении #1184007 писал(а):

Если в этом есть необходимость, вы можете зайти на сайт ВШЭ и найти в разделе "Сотрудники" порядка 50-ти гастербайтеров, закончивших средне и низко-рейтинговые западные университеты, но получающие зарплаты на порядок выше, чем, скажем, преподаватели МГУ. Фактически их зарплаты выше, чем в Оксфорде или Кембридже.

Можно привести в теме список поимённо хотя бы 20?

http://test.5top100.ru/index.php/university/work/HSE
Список в разделе 5. Не могу судить о математиках, но экономисты и гуманитарии - явно "несветила" в науке, чтобы убедиться в этом можно найти на сайте ВШЭ их сv и унылые списки публикаций.
Интересен п.3 - "информация о зарплате сотрудников конфиденциальна". Поскольку ВШЭ государственный вуз, то налогоплательщик вправе иметь информацию об уровне зарплат в гос.учреждении, не обязательно конкретных сотрудников, хотя бы среднюю зарплату (еще лучше интервал разброса). По крайней мере, так принято в "цивилизованных странах".
Представление об уровне зарплат можно иметь отсюда
https://aib.msu.edu/careercenter/2011/positions/477_TheHigherSchoolofEconomics(HSE).pdf
Немного старое объявление, 2011 г., но по тогдашнему курсу это примерно будет 6000 $ в месяц, неплохо для ассистента профессора. В Европе нет университетов, которые столько платят за такую позицию (может быть, только в Швейцарии и Люксембурге, где зарплаты повыше).
Так, например, по текущей позиции Lecturer по весьма модному направлению в Оксфорде предлагается заметно меньше.
https://www.ox.ac.uk/about/jobs/academic/index/ac22978j/

[Red_Herring]

dsge в сообщении #1184905 писал(а):

Не могу судить о математиках

Не моя специальность, но впечатление такое что

Цитата:

Вверх таких не берут, и тут.
Про таких не поют.

[Shtorm]

dsge, раз уж в нашей теме несколько раз прозвучало название "Высшая школа экономики", то возможно имеет смысл спросить вот о чём:
У нас на кафедре некоторые преподаватели считают, что ВШЭ является автором или соавтором целого ряда негативных реформ в высшем образовании России и являются "продолжателями" гайдаро-чубайсовских реформ в экономике России, но только в образовании, а не в экономике. Также и с других сторон я слышал примерно такое мнение о ВШЭ. Насколько это справедливо? И оказывает ли ВШЭ сильное влияние на российское образование в целом?

[Atmosfera]

Shtorm, не ВШЭ, а ректор её - Кузьминов. Он там какую-то комиссию возглавляет. Там в смысле в общественной палате.

[dsge]

Shtorm
Не инсайдер, не в курсе. Сужу по доступной публичной информации.

[EUgeneUS]

EUgeneUS в сообщении #1184724 писал(а):

Смогу поднять упоминаемую переписку (в которой был ссылка на задание) не ранее понедельника, 16.01.

Вот о чем была речь http://www.ctege.info/ege-po-matematike/probnyiy-ege-2016-po-matematike-18-s-otvetami-i-resheniyami.html задача 12.
Точек минимума сколько хочешь, но только одну можно записать в виде конечной десятичной дроби.
Судя по отсутствию скандала, задача так и осталась в тренировочных заданиях.

[GAA]

Shtorm — это я о своей писанине написал, что оффтопик, а так конкретные задачи ЕГЭ конечно обсуждать полезно. Я новое для себя узнал. Ну а моя писанина скорее не оффтопик, а «поток сознания».
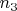
Первоначально я посчитал задание частным случаем размещения $n$ объектов по $r$ ячейкам (порядок объектов в каждой ячейке не важен). Число всевозможных размещений для четырех ячеек по $n_1$, $n_2$, $n_3$, $n_4$ объектов равно

$$C_{n_1, n_2, n_3, n_4} = \frac{n!}{n_1!n_2!n_3!n_4!}.$$

В нашем случае это $\frac{16!}{(4!)^4}$. Вероятность попасть некоторой команде в определённую ячейку равна $\frac{15!}{3!(4!)^3} \cdot \frac {(4!)^4} {16!}=4/16=1/4$. Так как нас интересует только одна команда, то множество элементарных исходов можно уменьшить (объединяя соответствующие элементарные исходы и складывая вероятности) до четырех исходов с одинаковыми вероятностями или до двух с вероятностями $1/4$ и $3/4$.

Приведенная схема решения продиктована заданиями типа «… найти вероятность того, что команда России попадёт во вторую группу, а команда Китая в третью.» В данном случае нас интересует две команды и множество элементарных исходов $\Omega = \{(i, j), i=1 \ldots 4, j=1\ldots 4 \}$, где $i$ команда России попала в группу $i$, $j$ — команда Китая попала в группу $j$. Т.е. имеем 16 исходов. Если считать эти исходы равновозможными (что неправильно), то вероятность каждого равна $\frac 1 {16}$. На самом деле вероятность исхода вида $(i, i)$ равна $\frac1 {20}$, а вероятность исхода вида $(i, j), i \ne j$ равна $\frac{1} {15}$.

Я не помню, чтобы в школе мне давалась схема размещения объектов по ячейкам. Но один из варианта вывода формулы для этой схемы как раз основан на переходе от схемы, где порядок объектов в каждой ячейки имеет значение (просто делим на $n_1! \, n_2! \, n_3! \, n_4!$). А перестановки в школе были. Т.е. я не считаю, что имеет смысл различать схему с $16!$ равновозможными исходами и с $16!/(4!)^4$ — они эквивалентны. (Кроме этого схема выборки без возвращения демонстрирует способ получения разбиения. Если капитаны тянут карточки не по очереди, то что мешает двум капитанам вытянуть одну карточку?)

И спасибо за терпеливые ответы в теме и ЛС. Я над ними ещё подумаю.

Теперь собственно оффтопик. Сама задача предполагает, что любые размещения 16 команд по 4 группам равновозможны. Насколько это разумно? Если в одну группу попадет 4 самых сильных команды и только победитель в группе продолжит состязания, то 3 из 4 сильнейших команд не смогут претендовать на награды… Почему разным исходам не задать разные вероятности?

В теме обсуждалась специализация школ. Доводы противников мне не понятны. На мой взгляд, идеальной является постепенная специализация. Для старших классов (9-11, если одиннадцатилетнее обучение в школе) можно сделать 4-7 вида школ (в зависимости от типа будущей специальности). Абитуриенты, закончившие определённый тип школы, могут без обучения на подготовительных курсах поступать на соответствующую группу специальностей. (После окончания бакалавриата тоже можно продолжить обучение не в любой магистратуре. Ну, по крайней мере, мне так говорили. Так что ничего особенного в специализации школ нет.)

Насколько я знаю, при обучении на математических факультетах это не нужно. Иное дело технические вузы и ФФ. На первом курсе параллельно изучается математика и физика (в первом семестре — механика). В лекционном курсе механики нужны двойные, тройные и криволинейные интегралы; простые дифференциальные уравнения — с этим лекторы как-то справляются: рассказывают идею и приговаривают, что строгое изложение будет дано математиками. За исключением криволинейных интегралов второго рода трудностей у студентов особых не возникает.
А вот на физическом практикуме, идущем во многих вузах параллельно лекционному курсу, необходимо выполнять оценки погрешностей «косвенных измерений» и строить доверительные интервалы для оценок параметров методом наименьших квадратов. И первую лабу надо сдавать через две недели после начала семестра. Вот тут тяжко.

[GAA]

Mikhail_K, --mS--, спасибо, теперь дошло. Редкостно притупил. Это о задачи с ЕГЭ.