STilda писал(а):
http://dxdy.ru/viewtopic.php?p=77549#77549Как насчет того, чтоб сменить алгебру чисел? кроме действительных и комплексных можно выдумать дикую кучу алгебр всяких со своими "мнимыми" единицами и правилами их сложения и умножения. в том числе не совместимых с "обычными".
Абсолютно невыполнимая вещь, но в качестве математических игр и развлечений можно. В компьютерных играх это используются
AD писал(а):
http://dxdy.ru/viewtopic.php?p=77552#77552Ну воздействовало, например, то, что не все натуральные числа являются четными. Вывести из теоремы Ферма вашу теорему для треугольника очень просто, а обратная импликация нетривиальна. Вы просто сформулировали более слабую теорему, заменив натуральные

четными.
Даже эту оценку я считаю для себя большим достижением.
.
Добавлено спустя 13 минут 39 секунд:
Элементарное доказательство теоремы ВТФ для треугольника
Теорема (ВТФ для треугольника). Если

означает, какое угодно, целое положительное число, большее, нежели 1, то ни для каких корней

и

уравнения

не существует треугольника с длинами сторон
 Доказательство
Доказательство. Пусть

и

- корни уравнения (1). Будем считать, что ни один из них не равен нулю, ибо треугольника в этом случае нет. Введем обозначения:

Подставляя в уравнение (1) вместо

, соответственно

, с учетом обозначений (2), получим тождество

Допустим, вопреки утверждению теоремы, что для этих корней существует треугольник со сторонами

и углами

, лежащими против соответствующих сторон. Для этой шестерки величин, по теореме косинусов, должны выполняться соотношения [5, 330]

При этом, для сторон треугольника, должны выполняться условия

которые, согласно обозначений (2), выполняются. А для углов треугольника должны выполняться свои условия

Но, одно из соотношений (4) должно совпадать с тождеством (3). Это совпадение можно получить только при единственном значении

из указанного в неравенствах (6) интервала для

. Подставляя это значение

в первое из соотношений (4), получим

При чем, первое из этих соотношений, совпадает с соотношением (3). Таким образом, если такой треугольник существует, то он должен быть прямоугольным.
Как известно [5, 329], для сторон прямоугольного треугольника должны выполняться неравенства:

тогда, по свойству неравенств и степени, должны выполняться и следующие неравенства

Следовательно, должны существовать треугольники со сторонами

и углами

, лежащими против соответствующих сторон и для каждой шестерки величин, по теореме косинусов, будут выполняться соотношения

одновременно с соотношениями (7). При этом, для сторон треугольника, должны выполняться условия:

которые, согласно обозначений (2), действительно, выполняются. Также должны выполняться и условия для углов треугольника:

Но угол

, лежащий против наибольшей стороны треугольника

не может быть острым, так как это будет противоречить последним двум неравенствам (8). Следовательно, условия для углов (11), должны иметь вид:

Но из первого соотношения (9) находим

То есть угол

.
Из сравнения условий (12) и (13) для

, приходим к выводу, что

, тогда условия для углов (12) примут вид:

то есть, для всех, указанных значений

, треугольники могу быть только прямоугольными. Подставляя

, в первое из соотношений (9), получим соотношения теоремы косинусов для сторон и углов, полученных треугольников:

Эти соотношения должны выполняться одновременно с соотношениями (7). Рассмотрим случай

, взяв из систем (7) и (14) первые соотношения

Будем рассматривать эти соотношения, как систему уравнений для неизвестных

и

. Для нахождения

и

, возведем обе части второго уравнения в квадрат. Получим

Вычитая из первого уравнения отдельно левые и правые части второго уравнения, получим

, откуда следует, что, либо

, либо

. Это означает, согласно обозначений (2), что либо
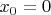
, либо

, что противоречит допущению. Тем самым доказано, что для значения

, треугольника, удовлетворяющего условиям теоремы, не существует.
Аналогично для случая

, получим систему

Сравнивая системы (15) и (16), замечаем, что добавление еще одного уравнения, не исключает решения, полученного для

. Этот вывод сохраниться и для

поскольку уравнения (15) будут содержаться в системе (14) для всех

. Следовательно, доказательство можно ограничить рассмотренным случаем.
Теорема доказана.
Следствие (ВТФ для отрезка). В условиях теоремы, не существует отрезка длиной

, для которого имело бы место соотношение
 Доказательство
Доказательство. Полагая в соотношениях (9)

и

, получим три одинаковых соотношения (17), что, в условиях теоремы, невозможно. Получили противоречие.
Следствие доказано.
Эта теорема – результат работы форума. Я не знал, какой она будет окончательной и, может быть, она еще измениться. Все зависит от ваших замечаний. Но, уже напрашивается вывод о некорректности формулировки ВТФ и бессмысленности поиска ее доказательства для целых положительных

.