Поскольку теоретику Петрову я больше доверяю , чем Вам, то несете бред именно Вы.
Вы ему доверяете, но ему же противоречите. Я с ним во всём согласен. Бред несёте именно вы, и читать вы до сих пор не научились.
Вы пока не привели ни одного.
Мизнер, Торн, Уилер, для начала.
Не предоставили. Вы голословно это утверждали, но хотелось бы конкретной теоремы. Если Вы сами не можете, то дайте точную ссылку, а не абстрактный параграф . SergeyGubanov поправил только Ваши формулы.
Конкретная теорема - это конкретные вычисления. Их предоставил я (не полные и с ошибкой), и потом
SergeyGubanov - исправил мою ошибку, и привёл другие недостающие формулы. Не хватает только формулы для ковариантной производной, но её ещё проще вычислить.
С формулами для

- вся теория будет полностью охвачена.
Я не все время сижу на форуме, приходится заниматься и другими делами, а так бы заметил.
С учётом того, что вы не способны на гораздо более простые вычисления, это заявление вызывает усмешку.
Дело в том, что , когда Вы нашли решение в координатах

:

, то при преобразовании сетки к другим координатам

по законам преобразования тензоров мы получаем

.
По этому поводу полностью отозвался
SergeyGubanov, и не вижу ничего, что бы стоило добавлять.
Вы , с помощью SergeyGubanov, дали другие преобразования (инфинитезимальные)
Конечные преобразования получаются как многократно повторённые инфинитезимальные. На строгом математическом языке - как экспонента от инфинитезимальных, где инфинитезимальные

лежат в алгебре, касательной к группе преобразований, а конечные

- лежат в самой группе.
Если же уравнения Гильберта-Эйнштейна также удовлетворяются относительно

, то это значит, что в одних и тех же координатах мы имеем 2 разных решения -

и
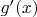
.
Ещё один бред. Координаты изменились, так что никакого "в одних и тех же координатах" уже нет и быть не может.
Хочу выступить в защиту формулы, приведенной Munin, поправка на ковариантную производную второго порядка малости. так как по порядку величины

и формула выглядит так

Нюанс в том, что не

а

Мы изначально можем стартовать из условий не с нулевой, а с конечной связностью. Поэтому, поправка первого порядка в формуле всё-таки будет, хотя вычислять её по новой связности или по исходной - разницы, конечно, нет (это уже будет отличаться на величину второго порядка).
-- 20.01.2014 18:44:53 --Не хватает только формулы для ковариантной производной, но её ещё проще вычислить.
С формулами для

- вся теория будет полностью охвачена.
Собственно, формула для ковариантной производной включает в себя только

так что вычислять больше ничего и не надо. Повторяю:
SergeyGubanov и я
полностью уже всё показали. (Строго говоря, в этой теме -
SergeyGubanov только, без соавторов. Я, технически, был только инициатором его вычисления. Но разумеется, эти выкладки известны в литературе, и в этой теме не оригинальны.)
-- 20.01.2014 18:47:11 --evgeniyМы изначально можем стартовать из условий не с нулевой, а с конечной связностью.
Вначале я тоже этого не сообразил, и поэтому ошибся. В калибровочных теориях без гравитации с этим проще.