Можно упростить вычисления, поскольку, по-видимому, имеет место:
(62) либо

, либо

является квадратом в кольце алгебраических чисел поля
![$\mathbb{Q}[\sqrt[5]{2}, i_5]$ $\mathbb{Q}[\sqrt[5]{2}, i_5]$](https://dxdy-01.korotkov.co.uk/f/c/a/c/cacfa2605a7e00311e95f4291d13333982.png)
.
В самом деле, число

является квадратом идеала в этом кольце, в котором, по видимому, имеет место единственность разложения на простые множители (что несложно проверить, например, в программе GP/PARI).
Значит,

является квадратом в этом кольце, где

- некоторый делитель единицы.
Мы показали, что произведение

является квадратом в кольце
![$\mathbb{Z}[g]$ $\mathbb{Z}[g]$](https://dxdy-04.korotkov.co.uk/f/b/f/e/bfec15f8b72d734ed990479e44472c4c82.png)
, и либо

либо

является квадратом в кольце
![$\mathbb{Z}[i_5]$ $\mathbb{Z}[i_5]$](https://dxdy-04.korotkov.co.uk/f/b/9/1/b91775ba913994676bc6d707666b676082.png)
.
Число

является делителем единицы, обладающим этими свойствами.
Можно проверить (62), вычислив другие фундаментальные единицы поля
![$\mathbb{Q}[\sqrt[5]{2}, i_5]$ $\mathbb{Q}[\sqrt[5]{2}, i_5]$](https://dxdy-01.korotkov.co.uk/f/c/a/c/cacfa2605a7e00311e95f4291d13333982.png)
, но мы пока не будем это делать.
Предположим, что (62) верно, и попробуем получить противоречие.
Если это удастся, то будем проверять.
Покажем, как в принципе можно получить противоречие из (62)
Во-первых, процитируем одно место из темы, которое нуждается в уточнении:
(42)





(по модулю простого идеала

).
Найдём коэффициенты при

в

:




Вычисления показали: все формы

равны нулю для всех 16 наборов параметров {

}.
Таким образом, подстановка в нулевые квадратичные формы нам ничего не дала.
Здесь речь идёт о простых делителях числа

. Пусть

- такой простой делитель. Казалось бы результаты вычислений не дают нам информации о коэффициентах

по модулю

.
Однако это не так. Не нужно забывать, что

- целые числа. Если

не существует по модулю

, то из (42) следует, что коэффициенты

(все кроме

) делятся на

. Этот вывод можно проверить для конкретных

, например,

, написав простую программу, в которой

пробегают значения от

до

, и

сравнимы с 0 по модулю

.
Рассматривая (62) по модулю

, мы не сможем получить противоречие, поскольку

может быть квадратом по модулю

.
Пусть теперь

является делителем не

, а числа

.
В этом случае, если

не существует по модулю

, то коэффициенты

(все кроме

) делятся на

.
Если
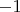
является квадратом по модулю

(например

), то рассматривая (62) по модулю

можно придти к противоречию.
Можно показать, что детерминант Вендта

не делится на

, из чего следует, что

делится на

.
Если

не делится на

, можно поменять

c

или

c

местами.
Однако, если теперь

- чётное, то

и

не являются взаимно-простыми, и мы не сможем получить (62).
Посмотрим, сможем ли мы преодолеть это препятствие.
Продолжение следует.