В этой теме, мы с
ananova займёмся подготовкой доказательства ВТФ для

.
Уважаемый
ananova, Вы в курсе, что в кольце
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
имеет место единственность разложения на простые множители.
Мы не доказали это, а нашли, используя математическую компьютерную программу gp/PARI.
Эта программа определила, что число классов идеалов кольца
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
равно 1.
Вы, возможно не знаете, что такое идеал, и тем более, что такое число классов идеалов.
Важно то, что если число классов идеалов равно 1, то имеет место единственность разложения на множители.
Когда мы найдём доказательство ВТФ для

, мы можем не доказывать эту единственность, а воспользоваться приёмом из моего доказательства для

.
Сейчас это не важно, важно то, что в кольце
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
можно не говорить об идеалах, поскольку все идеалы представляются обычными числами этого кольца.
Но если в кольце обычных целых чисел есть только два делителя единицы:

и

, то в кольце
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
есть и другие делители единицы, например
![$\sqrt[5]{2}-1$ $\sqrt[5]{2}-1$](https://dxdy-01.korotkov.co.uk/f/0/d/6/0d693244c2699de502188fffbac6d20282.png)
.
Если ненулевые, взаимно-простые целые числа

,

и

удовлетворяют уравнению Ферма:

, то

, где

.
Будем считать, что

- нечётное числом, а число

не делится на

.
Этого можно добиться, поменяв

,

и

местами.
Пусть
![$c=x^2-\sqrt[5]{4} y z$ $c=x^2-\sqrt[5]{4} y z$](https://dxdy-01.korotkov.co.uk/f/8/8/1/881276c19105bbe6658ef330300afbe782.png)
,
![$d=x^8+x^6 y z \sqrt[5]{4}+x^4 (y z)^2 (\sqrt[5]{4})^2+x^2 (y z)^3 (\sqrt[5]{4})^3+(y z)^4 (\sqrt[5]{4})^4$ $d=x^8+x^6 y z \sqrt[5]{4}+x^4 (y z)^2 (\sqrt[5]{4})^2+x^2 (y z)^3 (\sqrt[5]{4})^3+(y z)^4 (\sqrt[5]{4})^4$](https://dxdy-02.korotkov.co.uk/f/9/9/6/996237a7c84d838be7beaaaec0d635d782.png)
.
Не трудно доказать, что

и

- взаимно-простые числа, то есть единственными общими делителями этих чисел являются делители единицы.
Исходя из равенства:
(1)

,
взаимной простоты чисел

и

, и единственности разложения на простые множители, получим:
(2)

,
где

- делитель единицы, и оба числа

и

принадлежат кольцу
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
.
Используя приём из моего доказательства для

можно показать, что из (2) следует:
(3)

,
где число

принадлежит кольцу
![$\mathbb{Z}[\sqrt[5]{2}]$ $\mathbb{Z}[\sqrt[5]{2}]$](https://dxdy-04.korotkov.co.uk/f/7/f/9/7f937843babe3e28e780f5ecc2281f2582.png)
(мы ввели индексированное число

, поскольку оно может отличаться от числа

из (2)).
Наша задача: получить из равенства (3) противоречие.
Пусть

, где
![$g=\sqrt[5]{2}$ $g=\sqrt[5]{2}$](https://dxdy-03.korotkov.co.uk/f/a/6/3/a6377249ae5b3a7842963a15af0a431482.png)
, а

, ...,

- целые рациональные числа.
Тогда (3) можно записать в виде:
(4)

.
Обратите внимание на симметричную форму сомножителей в левой части равенства (4), которые переходят друг в друга при замене

на

.
Что касается числа

, то для нас важно только то, что это целое рациональное число (мы могли бы обозначить его через

, например, впрочем, нам не мешает его запись в виде

).
Oбозначим первый сомножитель в (4) через

, а второй сомножитель через

.
То есть:
(5)


Числа

,

,

,

(где

- комплексный корень пятой степени из 1) называются сопряжёнными с числом

.
Произведение всех сопряжённых чисел и самого числа

называется нормой числа

и обозначается:

.
Подобным образом, определяются сопряжённые числа с числом

, а также норма

.
Обратите внимание, что числа

и

- взаимно-просты (или их наибольший общий делитель равен

), поскольку их разность равна числу

, которое не имеет с

общих делителей, кроме

.
Определим число
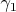
как произведение всех сопряжённых с

чисел (но, в отличие от нормы, не включая в произведение само число

).
Подобным образом определим и число

.
То есть:
(6)

,

В принципе, произведения в правой части равенств (6) можно преобразовать раскрытием скобок и получить выражение через коэффициенты чисел

и

.
В этих выражениях не будет числа

, которое исчезнет при использовании формулы

.
Но я не советую пробовать вычислить числа
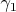
и

таким способом, потому что это непросто.
Есть гораздо более простой метод получить выражение, например, числа
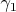
через коэффициенты

, ...,

,

.
Cуществуют формулы, выражающие норму

через детерминант матрицы коэффициентов числа

, а коэффициенты числа
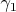
через детерминанты подматриц этой матрицы.
Наша первая с Вами задача, уважаемый
ananova доказать, что если присоединить к коэффициентам числа
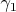
коэффициенты числа

, то все эти целые числа не могут иметь общих делителей (кроме тривиальных

и

).
Из этого можно вывести значительные следствия, например, что коэффициенты

, ...,

делятся на

, из чего можно вывести, что все эти коэффициенты (кроме

) делятся на

.
Я не знаю, пока, как получить из этих следствий и равенства (4) противоречие, поэтому и сказал, что наш успех "почти" гарантирован.
Что касается коэффициентов чисел
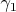
и

, я покажу Вам, как просто получить для них выражения на компьютере, и как доказать взаимную простоту всех этих коэффициентов.
Для этого Вам нужно будет проделать некоторые манипуляции, впрочем выкладки будет выполнять под вашим руководством компьютер.
Если Вы согласны принять в этом участие, я дам Вам дополнительные инструкции.