Цитата:
Тем более, что нет необходимости в предположении

делится на

для того, чтобы сомножители в левой части равенства (28 z) (умноженные на определённые числа), были квадратами.
Уберём это утверждении из предыдущего сообщения, так как мы сомневаемся в этом.
Пусть

- ненулевые, взаимно-простые числа,

, где

- нечётное простое число.
Пусть

делится на

.
Пусть

- чётное число, и имеет место равенство (3 z):
(3 z)
![$z^2-\sqrt[n]{4} x y=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$ $z^2-\sqrt[n]{4} x y=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$](https://dxdy-02.korotkov.co.uk/f/1/a/e/1ae34b04e2ad14367a8712569bc498a982.png)
, где

- целые числа.
Из этого равенства можно получить равенство:
(28 z)

,
где

,
![$g=\sqrt[n]{2}$ $g=\sqrt[n]{2}$](https://dxdy-01.korotkov.co.uk/f/4/1/3/4133b94ec39cc4ee7147cfe2693b71a382.png)
.
Пусть

, где

или
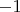
.
Тогда второй сомножитель в левой части равенства (28 z), делённый на

и помноженный на
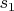
является примарным, то есть сравнимым с квадратом по модулю

числом.
Поскольку сомножители в левой части равенства (28 z) могут оба делиться только на степень

, и учитывая, что число

является квадратом, то из закона квадратичной взаимности Гекке следует, что второй сомножитель, помноженный на
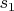
является квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
.
Значит и первый сомножитель, помноженный на
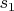
является квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
.
Помножим первый сомножитель также на

и сформулируем этот рtзультат:
(62.z.1) число

является квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, при условии однозначности разложения на простые множители в поле
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
.
Сформулируем (62.z.1) и по-другому, не предполагая однозначности разложения на простые множители:
(62.z.1 b) число

является квадратом целого алгебраического числа поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю любого нечётного простого числа

, которое разлагается в произведение главных идеалов этого поля.
Пусть

- нечётный простой делитель числа

, на который делятся не все коэффициенты

.
Пусть

разлагается в произведение главных идеалов поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
.
Мы определили

,
Пусть

.
Тогда

.
Из равенства
(3 z)
![$z^2-\sqrt[n]{4} x y=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$ $z^2-\sqrt[n]{4} x y=(a_0+a_1 \sqrt[n]{2}+a_2 (\sqrt[n]{2})^2+...+a_{n-1} (\sqrt[n]{2})^{n-1})^2$](https://dxdy-02.korotkov.co.uk/f/1/a/e/1ae34b04e2ad14367a8712569bc498a982.png)
следует сравнение
(3.z.1)

,
поскольку

.
Из (3.z.1) следует:
(3.z.2)

, где целое число

сравнимо с

по модулю

.
В самом деле

.
Пусть

- какой-либо простой идеал поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, делящий

.
Из сравнений (III) в теме "Поиск доказательства ВТФ для

обзорная тема 1", которые выполняются в силу леммы 2 в названной теме, и того, что не все коэффициенты

делятся на

следует, что не все числа

в равенствах (II) равны нулю.
Значит не все числа

сравнимы между собой по модулю идеала

.
Следовательно, часть из них сравнима с

, а другая часть сравнима с

по модулю идеала

.
Расположим числа

по кругу, так чтобы первое число следовало за последним.
Тогда обязательно некоторое число, сравнимое с

следует за числом, сравнимым с

, и некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Значит среди чисел

некоторое число, сравнимое с

следует за числом, сравнимым с

, и некоторое число, сравнимое с

следует за числом, сравнимым с

по модулю идеала

.
Нас интересуют числа

и

, соответствующие первому сомножителю в равенстве (28.z), умноженному на

.
Эти числа, сравнимые соответственно с

и

по модулю идеала

, являются квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, в силу (62.z.1).
Поскольку

и

, то числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю идеала

.
Поскольку

- произвольный простой идеал, делящий

, то числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
по модулю

.
Перемножая сравнения

, для

, где

- целое алгебраическое число поля
![$\mathbb{Q}[g, i_n]$ $\mathbb{Q}[g, i_n]$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3d9b1b57f4f0882a08385b1277a8f382.png)
, получим:
(70.z) числа

и

сравнимы с квадратами целых алгебраических чисел поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
по модулю

.
Мы не сможем получить противоречия из утверждения (70.z) для конкретных простых делителей

числа

по той причине, что коэффициенты

делятся на все эти кoнкретные

.
Мы показали, что нечётное число

не может делится на эти кoнкретные

, рассматривая второй множитель равенства (28), помноженный на

, по модулю

.
Но с чётным числом

и вторым множителем равенства (28.z), помноженным на
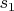
такое рассуждение не проходит.