Под-тема:
Числовые методы и теория Галуа.
Не будем рассматривать радикальное расширение, так как для числового решения уравнения это не нужно. Остановимся на свойствах симметрии и цикличности группы Галуа.
Возьмем произвольное уравнение n степени:

Найдем функцию подставки, при которой коэффициенты останутся на своем мести. Такую подставку можно выразить через функцию, полученную из дифференциального уравнения


, где

. При любом

мы можем однозначно выразить коэффициенты уравнения выразить через константы функции, отобразив коэффициенты на функции. Мы получим систему из

уравнений с

неизвестными:

Через эту функцию можно выразить и корни этого уравнения:

Получили симметрию. Коэффициенты и корни выражаются через одну функцию.
Есть еще один вид симметрии. Коэффициенты можно выразит через функцию
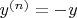
. .
Если надо выразить одновременно корни уравнения и его коэффициенты можно использовать уравнение

. Характеристическим уравнением для него будет

.
Цикличность связана как с цикличностью корня из единицы

, так и с цикличностью функции

. производная которой равна самой функции

. Это дает возможность рассматривать связать свободный коэффициент и корень функции через дифференциальное уравнение

.
Цикличность дает возможность включить равенство в числовой метод

. Если вместо

в формулу Виета подставить

мы можем понизить степень уравнения:

Или этот метод получился, аналогичен методу Ньютона.
Применение в физике.
В основе метода лежит элементарная алгебра. Элементарная алгебра одна из немногих теорий в математики, для которой доказана ее полнота и разрешимость.
В 1951 году А.Тарский методом исключения кванторов существования доказал полноту и разрешимость элементарной алгебры. В 1936году доказана теорема Тарского, где доказано, что понятие арифметической истины арифметически неопределимо.
Мендельсон Э., Введение в математическую логику, «Наука» 1976.
Законы элементарной алгебры не зависят от аксиом свойств. Это дает возможность использовать ее в других разделах математики и с ее помощью применять выводы, сделанные в одних теорий к другим теориям.
В физике есть закон, в основе которого лежит свойства элементарной алгебры. Это закон сохранение энергии.
Элементарная алгебра дает возможность через функции объединить все геометрии параллельности. Евклидову геометрию, геометрию Лобачевского и геометрию Римана.
Цикличность дает возможность на основе зависимостей выводить формулы.
В математики элементарная алгебра вводя аксиомы свойств, дает возможность строить новые теории, а в физики это будут постулаты и физические постоянные.