Метод состоит в том, что бы для уравнения n-й степени

ввести как характеристическое дифференциальное уравнения

. Тогда коэффициенты данного уравнения можно выразить через функции, полученные при решении дифференциального уравнения.
Пример:

,
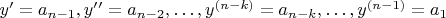
. При

мы получим систему из

уравнений с

неизвестными. Система будет однозначно разрешима относительно коэффициентов

. Так для квадратного уравнения

будем иметь:

Систему можно построить не только для коэффициентов, но и для корней уравнения. Если

,

, то получим:

Этот метод не зависит от системы координат, он зависит только от свойств функции полученной при решении дифференциального уравнения. Частные функции линейно независимы. Это делает его универсальным. Он может применяться в любой теории независимо от того как там представлены единицы измерения.
Для чего это делается? Для того чтобы применить еще одно свойство дифференциального уравнения

. Цикличность единиц измерения.
Несмотря на то, что количество соотношений между

единицами измерения будет равно

благодаря цикличности их всегда можно свести к числу количества коэффициентов в уравнении

степени.
Мы имеем для уравнения n-й степени

корней. Тогда выразим соотношение между свободным членом этого уравнение и его корнем через квадратное дифференциальное уравнение.

,

,

.
Тогда получим:

Возможность свести многомерное измерение к двухмерному, является доказательством, что законы физики не изменяются от числа измерений. В то же время, применяя дифференциальное к конечному измерению можно вывести закон зависимости качества от количества. При этом надо учитывать, что корни характеристического уравнения должны быть действительными.
Есть еще одно свойство применение дифференциальных уравнений в физике. Это возможность выразить две величины через два дифференциальных уравнения:

и

Частным случаем при решении второго дифференциального уравнения является волновая функция. Но не только это. Возможность выразить одни и те же величины через различные функции дает возможность выразить зависимость между дискретными и волновыми свойствами через евклидову геометрию.