Методика более широкое понятие, чем модель. Одна и та же методика может применяться для различных моделей. Например: метод системы координат геометрически или аналитический метод и т.д. В то же время различные методы могут приводить к одинаковым результатам. Обычно применение метода связано с его свойствами. Свойства метода, который я предлагаю, связан со свойством цикличности корней из единицы

,

и с линейной независимостью частных функций.
Рассмотрим конечную группу подстановок n степени. Так как каждый элемент группы может переходить сам в себя, то мы можем выразить это через функцию, которая является решением дифференциального уравнения

. При

мы получим однозначное отображение элементов группы на коэффициенты функции т.к. получим систему из n уравнений с n коэффициентами. Элементы группы постоянные величины или инвариантны. Там где есть инвариант, ищи симметрию. Предположим, что элементы группы могут преобразовываться в обратные элементы. В рамках самой теории групп это не возможно выразить, так как обратные элементы не входят в рассматриваемую группу. Но можно варазить через функцию. Выразим это по аналогии дифференциальным уравнением

. Тогда при

мы получим однозначное отображение элементов группы на коэффициенты функции.
Рассмотрим группы

степени как элементы принадлежащей группе

. Тогда при функциональном отображении мы получим сложную функцию. Так внутренняя функция циклична то можно дифференцировать только по внешним параметрам. При

получим две функции

,

. Эти функции основаны на симметрии

,

.
Имеешь симметрию, ищи инвариант. Возьмем в качестве инварианта физические постоянные. Постоянную Планка, предельную скорость света, и гравитационную постоянную.
Сначала заметим, что эти уравнения являются описанием двухмерного пространства. При

получим

,- трансляция и

,- поворот.
Свяжем между собой различные функции и единицы измерения.
В КМ постоянную Планка мы можем выразить через две функции которые связывают с свойствами частиц. Корпускулярные свойства и волновые свойства частицы.
В СТО время не есть понятие независимое от понятия пространства, здесь все измеряется скоростью. Значить нам нужна функция в котором были связаны трансляция и поворот. Таким требованиям отвечает гиперболическая функция.
Дж. Уилер в книге «Гравитация, нейтрино и Вселенная» утверждает что масса тоже длина только выраженная другим способом. Мы знаем, что масса Солнца отклоняет проходящий вблизи него луч света. Степень отклонения определяется массой Солнца и расстоянием от центра до этого луча. Зная степень отклонении луча и расстояние, на котором луч проходит от Солнца, можно вычислить Солнечную массу, оперируя только этими величинами. В этом случаи Солнечная масса равна

сантиметра.
Достаточно умножить этот результат на квадрат скорости света и разделить на гравитационную постоянную, чтобы вернуться к привычной нам массе Солнца, равной
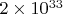
граммам.