Гаджимурат писал(а):
Напомним( приняли условие,что

) :
Что это означает? Если "

делится на

", то пишите, как принято:

(
bot вам уже говорил об этом). Вам что, трудно палочки ставить? Если же эта запись означает что-то другое, то объясните - что.
Гаджимурат писал(а):
1.

, здесь

и

.
2.

.
3.

.
4.

.
5.

.
6.

.
7.

.
Знаем,что

и

делятся на

и

.

.
Докажем,что для любых степеней

.
Из ур-ния (6) следует:

. В ур-нии (7)

заменим на

(здесь напомним,что

), так-же поступим и с

, а

и, отбросим все члены,содержащие

, имеем:

-делится на

, а так как

и

-делится на

.

разделим на

и произведя необходимые преобразования,отбросив все члены,которые делятся на

и более,а

и зная,что

делится на

,т.как

, можем записать:

делится на

и,разделив на

, имеем:

(8) -делится на

(здесь принято

). Из (6) имеем:
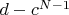
делится на

(9),поэтому из (8) вычтем (9), имеем:

делится на

(10). Примем:

, поэтому из (10) следует :

делится на

и

делится на

(11). В Ур-нии (4)

заменим на

и, отбросив все члены,которые явно делятся на

и более, имеем:

делится на

и

делится на

,тогда и

делится на

(12). Из (12) вычтем (11) , имеем:

и

делится на

. Отсюда и

делится на

.
Мы доказали : решение ур-ния Ф. в целых числах возможно при условии, что

делятся на

(для всех простых степеней

) т.есть мы доказали

. Второй этап доказательства ВТФ закончен.
, стоп! Мы же, кажется,
договорились, что вы ограничитесь (пусть,
пока) случаем

. Вот и излагайте свои вычисления для

. И не забудьте в оформлении учесть мои
замечания. Я считаю, что вы еще не закончили 1-й этап - я увидел лишь некие начальные определения и
начало рассмотрения некоторого
плохо обоснованного случая (

) ВТФ при

. Закончите, пожалуйста, рассмотрение этого случая - затем займемся и другими случаями, пропущенными (осознанно или неосознанно - не знаю) вами.