Формулировка теоремы в правильном её понимании проста. Если натуральное число

, то уравнение
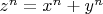
нельзя решить в целых натуральных числах (при

такие решения существуют, например, при x=3, y=4, z=5).
Доказательство Великой теоремы Ферма выполнил с помощью «метода подъёма»: «Для доказательства нерешаемости в целых числах уравнения с разложением на два слагаемых в той же степени мы предлагаем метод, противоположный ранее предложенному нами методу спуска, с помощью которого нам удалось обогатить математику целых чисел. Предлагаемое же доказательство сформулированной нами теоремы разложения степеней основывается на методе подъёма)».
До сих пор не понимают, что подразумевал Ферма за этой «литературной условностью» (сам он не разъяснил сути своего метода доказательства) и предполагают, что он ошибся в своём «удивительном доказательстве», а ошибка кроется в его гипотетическом «методе подъёма».
Дальше идёт моё вышеизложенное доказательство.