Не существует никакой суммы кубов, которая делится нацело на числа

,

,

, и ее основание не содержит данных чисел.
Переводя на формальный язык, вы утверждаете, что если 17 делит

для целых

, то оно также делит

. И аналогично для 29 и 71.
Эти утверждения легко следуют из разложения:

Дело в том, что, если простое

делит второй множитель и

не является квадратичным вычетом по модулю

, то оно обязано делить оба числа

и

(а, значит, и их сумму

).
Как нетрудно,

не является квадратичным вычетом по модулю простого
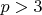
если и только если

.
Таким образом, ваше утверждение справдливо, например, для следующих простых

в пределах первой сотни:
5, 11, 17, 23, 29, 41, 47, 53, 59, 71, 83, 89