(Даёшь бурбакизацию в школьную программу?)

[ozheredov]

Считается, что в серьёзных школьных предметах типа математики надо сразу взять учеников в клещи железных фактов: смотри, две палочки плюс три палочки будет столько же, сколько три палочки плюс две палочки - на колени перед неопровержимой истиной! Аргумент:

wrest в сообщении #1712836 писал(а):

ТС, увы, не Гильберт, который говорил что вместо плоскостей, точек и прямых можно говорить про столы, стулья и пивные кружки.
Подход к изучению алгебры как, скажем, какого-то иностранного языка, как раз и приводит к выводам типа $\sin x + \sin x=\sin 2x$

Однако, например, дети неплохо так научаются играть в шахматы. Никто не обосновывает им через жизненный опыт, что конь должен ходить буквой Г, а пешка может брать на пароходе проходе. То есть шахматы как бы висят в воздухе, существуя отдельно от реального мира, где надо считать сдачу в магазине и чинить протекающий толчёк. Но не смотря на это, повседневный опыт не существует отдельно от шахмат, потому как что наша жыыызнь? Играаа, и эта игра - шахматы. Может, тогда имеет смысл честно рассказать им про матан? Аргумент:

ozheredov в сообщении #1712845 писал(а):

математика абстрактная наука, не имеющая ни малейшего отношения к калькуляторам, яблокам у Саши и Маши и прочим предметам из "объективной реальности" (с). Любые бытовые вещи могут иметь отношение к математике, но эта любовь сугубо односторонняя, осуществляемая через некую абстрактную сущность под названием "модель". Дети успешно изучают шахматы, хотя прекрасно понимают, что никакая "объективная реальность" (с) не подскажет им правила, по которым ходит конь (в отличие от яблок Саши и Маши, которые ЯКОБЫ подсказывают (на самом деле нет), что 2+3=5). Более того, вместо коня можно поставить на доску пивную кружку пуговицу (если конь потерялся), и ни у кого не возникнет никаких вопросов. Калькулятор говорит, что два синуса икс не равно синусу от двух иск? А если я переключу его в двоичный режим, то $1 + 1 = 10$.

[Mihr]

ozheredov, странный выбор Вы предлагаете: один из двух крайних случаев. Которые одинаково неуместны в школе. Вы не допускаете возможности промежуточных вариантов?
Да и вот это:

ozheredov в сообщении #1712848 писал(а):

на колени перед неопровержимой истиной!

никакого отношения к реальности не имеет. Никто школьников на колени не ставит. Ни в буквальном, ни в переносном смысле.

[Anton_Peplov]

ozheredov в сообщении #1712848 писал(а):

Однако, например, дети неплохо так научаются играть в шахматы.

В шахматах нудный этап усвоения правил занимает не так много времени, после чего начинается игра, азарт, желание победить противника, сожрать всех его коней с таким прекрасным аппетитом.

Теперь представьте, что:
- в шахматах несколько сотен или тысяч разных фигур и соответствующее количество правил, причем чуть ли не на каждом уроке детям нужно усвоить новый вид фигур или новое правило, как они ходят;
- в шахматы невозможно играть и побеждать, а можно только решать шахматные задачи;
- в связи с обилием фигур и правил даже задачи вроде "поставь мат в три хода" будут редкостью, а в основном знакомство детей с шахматами будет состоять в решении унылых задач типа "допрыгай конем/слоном/кораблем/кракозяброй из пункта А в пункт Б", направленных на закрепление только что выученных правил.

Будут ли дети мотивированы усваивать правила таких шахмат, если не будут понимать, зачем это нужно?

[Mihr]

И вот это, кстати, совсем уж странно:

ozheredov в сообщении #1712848 писал(а):

А если я переключу его в двоичный режим, то $1 + 1 = 10$.

Мне кажется, это довод примерно такого типа: "Если я напишу и по-русски, а затем прочитаю по-английски, то окажется, что это не и, а ю. Ну, а если по-армянски, то вообще с".

[wrest]

ozheredov в сообщении #1712848 писал(а):

Однако, например, дети неплохо так научаются играть в шахматы.

Насколько я себе представляю, очень немногие. Конечно, дети разные бывают. В теме из которой выросла эта, ТС ясно называет себя "отстающей". А вы про абстракции... Стыдно, товарищ!

ozheredov в сообщении #1712848 писал(а):

Может, тогда имеет смысл честно рассказать им про матан?

Может, но не всем. На мой личный взгляд (я не специалист по педагогике вообще и математической в частности), преподавание математики через отношение к реальной жизни правильное. Сначала говорят о натуральных числах. Потом оказывается, что есть отрицательные и теперь это целые числа. Потом оказывается что нужны рациональные, затем выясняется что раыиональные это ещё не всё, есть иррациональные, и под конец - комплексные. Ну вот так арифметика, в целом, и развивалась исторически. $\mathbb{N} \to \mathbb{Z} \to \mathbb{Q} \to \mathbb {R} \to \mathbb{C}$
Про матан надо рассказывать тем, кто это хочет и способен слушать (в матшколах, факультативах в школах, ну и студентам естесвеннонаучных специальностей вузов).

[Mihr]

wrest в сообщении #1712853 писал(а):

Потом оказывается, что есть отрицательные и теперь это целые числа. Потом оказывается что нужны рациональные

Вообще-то, наоборот. Школьников сначала знакомят с дробными числами, а уж затем - с отрицательными.

-- 19.12.2025, 14:02 --

Исторически, кстати, это тоже так: дроби возникли гораздо раньше отрицательных чисел.

[warlock66613]

Шахматы-то как раз очень даже реальны: вот, стоят на доске, можно потрогать. Вот чтобы и числа были реальны, нужны палочки.

[wrest]

ozheredov в сообщении #1712848 писал(а):

Калькулятор говорит, что два синуса икс не равно синусу от двух иск? А если я переключу его в двоичный режим, то $1 + 1 = 10$.

Алгебра, конечно, производит отделение чисел от их записи в какой-то конкретной системе счисления, но в любой системе счисления $\forall x \to \sin x + \sin x = \sin 2x$ не является верным в общем случае (при общепринятом определении функции $\sin(x)$ ).

[alesha_popovich]

ozheredov
за что вы так детей ненавидите? Лучший способ заставить детей ненавидеть математику (которую многие и так то не очень любят, мягко скажем) - это заставить их заниматься подобной абстрактной дичью. Пусть лучше на яблоках учатся, там хоть можно сделать уроки интересными с живыми примерами - при желании учителя, конечно. А бурбакизацию оставьте для физмат классов, т.е. тем, кто осознанно туда пошёл.

[Cos(x-pi/2)]

Возможно, моё впечатление о той теме (Элементарная алгебра для отстающих) поверхностное, так как полностью её не читал, но выскажу предположение, что одна из главных причин затруднений у той девушки-топикстартерши - незнание правил определения порядка действий в алгебраических выражениях.

Про пример с синусами Dedekind так ей и ответил: "Это просто приоритет выполнения операций." UPD: об этом там написал и Лукомор.

В той теме много отвечающих, я туда не буду вмешиваться, но посоветовал бы отвечающим детально продумать подходящий текст и чётко и подробно написать всё о порядке действий. Т.е. ТС должна усвоить, что речь даже не "просто" о приоритете операций в данном частном случае, а что в алгебре вообще приняты строжайшие правила, которые надо выучить в первую очередь, железно помнить, и применять во всех примерах.

Пока же ТС, по-видимому, смотрит на формулы как на слова обычного языка: просто читает буквы слева направо. Надо ей на примерах объяснить, что главное это скобки, т.е. надо сначала смотреть, есть ли скобки, и что есть внутри них. Скобки бывают внутри скобок внутри скобок и т.д., и действия внутри самых внутренних скобок выполняются в первую очередь. Простой одиночный аргумент функции часто пишется без скобок лишь для экономии типографских знаков, но скобки подразумеваются; а когда аргументом является сложное выражение, то скобки строго необходимы. Считается, что функции вычисляются до того, как с ними выполняются остальные действия, такие как умножение, сложение и т.п. И для этих действий тоже установлен строгий порядок: если не написаны скобки, то сначала делается возведение в степень (что можно рассматривать и как вычисление функции), затем умножение или деление, затем сложение или вычитание.

Это я написал сумбурно, навскидку, но надо бы подобного рода текст и примеры хорошо продумать и согласовать с изложением в школьных учебниках. Может быть, если такого рода правила подробно перечислить в той теме, да с разнообразными примерами, то это и будет почти вся школьная алгебра; а ТС, если их выучит, то из "отстающих" сразу превратится в "успевающую" :)

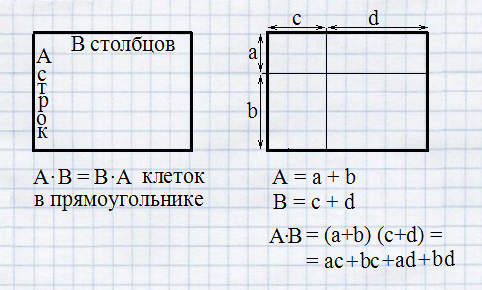
Калькулятор, конечно, не годится для пояснений; это чёрный ящик. А "счётные палочки", или, что намного удобнее для самостоятельных экспериментов, - клетки на школьной тетрадной бумаге "в клеточку", - очень даже годятся. И для рисования графиков, и для иллюстрации несложных действий. Пример:



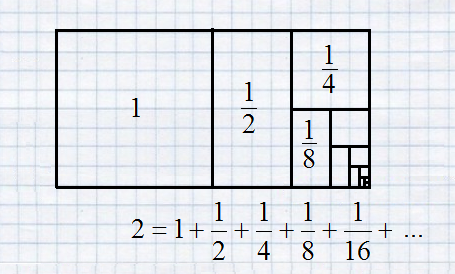
Вспомнился ещё наглядный пример из какой-то книги, которая попалась на глаза в молодости (и сразу тогда поверил, что суммы бесконечного количества слагаемых бывают конечными; тем самым парадокс Зенона об Ахиллесе и черепахе отпал :)



Вообще визуализации не только полезны, а и, наверное, необходимы для освоения математики на простом физическом уровне понимания: "тригонометрический круг", график параболы в связи с корнями квадратного уравнения, вообще графическая иллюстрация решений уравнений, ученик должен обязательно строить и изучать графики функций (в этом деле калькулятор может быть полезен). В дальнейшем - производная функции как "наклон касательной к графику", определённый интеграл как "площадь под кривой". Векторы - как "стрелочки" на чертежах, со своими правилами действий. Комплексные величины тоже допускают наглядное представление - "стрелочки" на плоскости.

[wrest]

Cos(x-pi/2) в сообщении #1712875 писал(а):

Калькулятор, конечно, не годится для пояснений; это чёрный ящик.

Зато он годится для немедленной проверки правильности ответа, ну и выкладок. И как мне кажется, убережёт ТС от вопросов типа

horda2501 в сообщении #1712772 писал(а):

Тогда в $\sin(x-4\pi)=\sin (x-2)$?

-- 19.12.2025, 21:24 --

Cos(x-pi/2) в сообщении #1712875 писал(а):

В той теме много отвечающих, я туда не буду вмешиваться, но посоветовал бы отвечающим детально продумать подходящий текст и чётко и подробно написать всё о порядке действий.

Пробовали, например:

Rak so dna в сообщении #1613132 писал(а):

Cначала выполняем действия в скобках, потом возведение в степень, потом умножение/деление, потом сложение/вычитание. Если действия имеют одинаковый приоритет, выполняем их слева направо.

Ответ такой:

electron2501 в сообщении #1613170 писал(а):

Извините, но на данный момент я уже не могу думать головой

И дальше обнуление.

Поэтому я там и напираю на калькулятор. Чтобы ТС обрёл связь с реальностью, чтобы указать на то, что буквы это всё-таки образы чисел, и дать инструмент самопроверки.

[Cos(x-pi/2)]

wrest, от ошибок указанного Вами типа уберегает (и при этом способствует именно пониманию!) размышление над чертёжиком с тригонометрическим кругом. Калькулятор не научит понимать формулы.

А если та ТС не хочет или не может думать головой, то тогда бесполезны вообще любые попытки помочь ей изучать алгебру.

[wrest]

Cos(x-pi/2) в сообщении #1712886 писал(а):

Калькулятор не научит понимать формулы.

Я же не писал, что научит. Я писал другое.
Могу сказать, что калькулятор научил меня многому, когда я учился в школе. Сперва обычный, потом МК-54. Но я, правда, не был отстающим и математику поглощал с удовольствием, а не через силу.

Впрочем, вы можете попробовать сами в той теме и проследить за результатом

-- 19.12.2025, 22:00 --

Cos(x-pi/2) в сообщении #1712886 писал(а):

А если та ТС не хочет или не может думать головой, то тогда бесполезны вообще любые попытки помочь ей изучать алгебру.

Там какой-то необычный случай. Чувствуется некоторая воля, но при этом невосприимчивость к советам.
Я вообще не думаю, что ТС тот, за кого себя выдаёт (отстающую школьницу).

[Cos(x-pi/2)]

Не спорю, что калькулятор бывает нужен. Например, калькулятор полезен при расчёте по какой-то формуле числовых данных для таблиц. В том числе - таблиц для построения графиков функций. Или для расчёта чего-то по данным измерений в лабораторной работе.

Но проверять алгебраические формулы надо учиться с помощью алгебраических же преобразований, выкладок; надо учиться придумывать удобные для проверки частные случаи, в том числе случаи, когда должен получиться заведомо знакомый результат, разные предельные случаи (например, когда ответ заведомо должен обратиться в ноль или устремиться к бесконечности), и всё такое.

[wrest]

Cos(x-pi/2) в сообщении #1712888 писал(а):

Но проверять алгебраические формулы надо учиться с помощью алгебраических же преобразований

Ок, надеюсь вы попробуете научить ТС той темы чему-нибудь
Ну, чтобы составить собственное практическое мнение о применимости в конкретном случае.

Хочу ясно подчеркнуть: я считаю, что калькулятор был бы чрезвычайно полезен конкретно ТС той темы. А не как универсальный совет каждому ученику на любой случай.