математическая логика имеет дело именно с формальным языком, а рассуждения ведутся, как и в других разделах математики, на метаязыке, т.е. обычном языке, с использованием обычной логики
Я не очень понял, что значит "рассуждения ведутся на метаязыке". По моим понятиям "метаязык" - это язык, на котором мы определяем другой (прикладной) язык. Отсюда и приставка "мета" - она подразумевает, что есть язык какого-то более низкого уровня (в смысле идущей "вверх" иерархии мета-мета-...). Например, правило modus ponens невозможно записать в языке исчисления предикатов первого порядка. Но если использовать метаязык, содержащий символ выводимости, то можно:
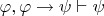
.
В каком смысле мы должны считать естественный язык за "мета"? У нас просто есть некоторые понятия о том, что сказанное является "утверждением" (а не бессмысленным набором символов или звуков), и у нас есть некоторые понятия о том, что последовательность утверждений (т.е. "рассуждение") следует или не следует некоторым правилам "корректного рассуждения". Да, эти правила иногда могут завести нас в тупик, тогда мы их уточняем. Когда мы хотим объяснить эти правила другим людям, то пытаемся их сформулировать более или менее однозначно. Когда это не получается на том языке, который мы используем обычно, мы его расширяем, вводя дополнительные слова типа "следует", "всегда" или "некоторые". С какого момента такой язык должен считаться за "мета"? При определении формальной системы на основе исчисления предикатов потребность в метаязыке появляется, например, когда мы осознаём, что для записи правила вывода потребуется новый символ - "выводимости", отличающийся от символа импликации. Может быть и естественный язык нужно начинать считать "за мета" с того, момента, как мы догадались, что слово "выводится" не является синонимом слова "следует", а является "метатермином"?
-- Сб авг 30, 2025 13:51:36 --Поэтому утверждение "последователь любого натурального числа не является нулём" не имеет отношения к реальной арифметике.
Правильно ли я понял, что таким образом Вы предлагаете считать за "реальную арифметику" подмножество утверждений арифметики Пеано, содержащее только утверждения о равенстве или неравенстве замкнутых термов, плюс, может быть, логические связки между ними? Но точно без переменных и кванторов?
Возможно выражусь более ясно, предлагается рассматривать арифметику (счетную способность) человека как экспериментальный факт, а далее, как в физике, над этим можно строить теории, которые можно проверять на конкретных примерах. В целом ничего нового, по факту так и делается. Но многие математики почему-то забыли, что их деятельность верифицируется не только по принципу теория другой теорией, а теория практикой.
Я хочу заметить, что в языке арифметики Вы можете записать исключительно из констант и операций над ними такие сложные выражения, что замучаетесь проверять их "экспериментально". Тем не менее, нельзя будет сказать, что это "принципиально" невозможно.
Я полностью согласен с Вами, что теории существуют не сами для себя, а для использования на "практике". Тем не менее, я не понимаю, чем Вам не полюбились обобщающие утверждения, проверка которых "на практике" всегда будет неполной, как мы ни старайся?
-- Сб авг 30, 2025 14:17:31 --Вы, неощутимым для себя образом, стали выдвигать требование давать философские определения (а "предмет науки" - это термин из философии науки) языком с формальной грамматикой какого-то там уровня.
Это очень ощутимо, ибо с философскими определениями я не хочу иметь дел ввиду их неадекватности и неоднозначности. А что касается формальных грамматик, то там более или менее всё ясно.
Символы "1" и "7" на автобусе не имеют никакого отношения к натуральным числам.
Речь не о символах, а о числе 17, которое, как я вижу, является номером маршрута данного автобуса.
Вот эти кавычки и "т.н." как раз и указывают на Ваши, хмм, особые отношения с реальностью.
Это кавычки и "т.н." указывают всего лишь на то, что эта классификация - условность, а не какая-то абсолютная истина.
Как только Вы начали считать сдачу и-или планировать расходы - так сразу процесс "бухгалтерия домохозяйства" появился.
Не выдумывайте. Когда я считаю суммарную стоимость покупки, то я просто считаю стоимость покупки. Никакого процесса ведения бухгалтерии домохозяйства не появилось. А как я планирую расходы, то Вам неведомо. Могу сказать, что почти никак.
"Уничтожение спичек в костре - это некорректная постановка эксперимента" и "Уничтожение спичек в костре не описывается арифметикой" - разные. В них переставлены причина и следствие.
И что здесь причина, и что следствие?