Начнём с окончания Вашего вчерашнего комментария:
Если набор чисел
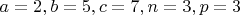
не годится для опровержения построения раздела 4, покажите, пожалуйста, где именно; я с ходу не вижу
Ошибка здесь. Если Вы выбрали

, то таких остатков, как

и

не существует.
Все остатки, которые Вам нужны в
общем случае, Вы берёте из диапазона от

до

. Т.к., 0 исключён, тогда "Ваш" диапазон -от

до

. Т.е., это

и

. И это всё, для

. Первое.
Второе: обычно рекомендуется брать "большенькие"

-там больше возможностей. Для

их больше, чем для

. И т.д. Говоря совсем уж простым языком, остатки, которые используются Вами для анализа, это цифры соотвествующей системы счисления.
Третье: Лучше писать (и работать) не с записью

, подразумевая, что это
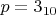
(в десятичной системе счисления), а с такой записью:
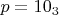
. Соответственно, и для других систем счисления. Это было бы понятнее Вам самому, я думаю, когда Вы будете находить остатки от деления и Вы быстрее будете получать результат.
Идём дальше вверх по Вашему второму ответу.
Я приведу пример, а Вы укажите, где именно он не проходит
Я мог бы тоже приводить пример(ы)(если захотите-
напишите), а по Вашему Примеру, считаю, что мы разобрались. Эта уверенность , я думаю, появится и у Вас после моих Примеров. Но, прежде, чем писать мои Примеры, я ещё раз хотел бы Вас вернуть к примитивным Пифагоровым Тройкам. [Что Вы сразу хватаетесь за степени

? Я предлагал и предлагаю разобраться Вам сначала с тем, что лежит перед Вашими глазами-с Пифагоровыми Тройками и понять, что такое

. Ниже дам определение для

.] Посмотрите на представленный там Пример. Зачем Вы пишете мне эти фразы:" в теме помимо Вас ещё как минимум двое участников излагают свои построения, и кто кому на что отвечает вычленять очень трудно."? Я в моём личном послании Вам указал на конкретный мой комментарий с датой и временем. При каких делах здесь другие участники и их "построения"? Я это не понимаю. Пример мой с Пифагоровыми Тройками разбрали бы сначала, а не "построения" или общение кого-то ещё и с кем-то ещё...
Итак,
 это число, которое умножается на
это число, которое умножается на  , и при прибавлении остатка самого числа даёт само исходное число
, и при прибавлении остатка самого числа даёт само исходное число. Если у Вас есть два числа

и

, то, соответстветственно, для Вы имеете

, как

и -

в десятичной системе счисления и в

. Представим эти исходные числа в

-ричной системе счисления и это запишется так:
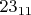
и
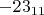
. Мы будем иметь

для первого и -2_{11}-для второго числа. Умножение на

для первого числа и прибавление остатка

даст исходное число.
При этом, имейте в виду, что p-адическая запись для отрицательных чисел будет совершенно иной, чем представленная обычная запись. Я дам соответствующую ссылку в личке, чтоб Вы разобрались...
Я понимаю, что Вы всё это знаете и, скорее всего, лучше меня. Я намеренно вернулся к этим элементарным вещам, если уж возникло такое недопонимание по

. Поэтому, я сегодня пошлю Вам в личке ещё один пример-для разных степеней-это квадраты, кубы и 6-ые степени. Вы это могли бы разобрать самостоятельно более детально. Там всё указано-что есть что... Здесь же,
если скажете, я готов выложить часть тех Примеров в виде выражений для уравнения ВТФ по модулю 31.
Далее.
я хочу конкретно вцепиться в озадачивающее меня построение раздела 4.
-Звучит , как-то угрожающе?..:)) Что значит "вцепиться"? Тем более, это:
для опровержения построения раздела 4
-Вы вчера говорили о желании получить понимание. Я, конечно, заинтересован и в "опровержении", как факте, но совершенно не заинтересован
в собственном участии в этом процессе! :)) Надеюсь, это понятно? Если Вы так ставите вопрос, то я мог бы сказать: разбирайтесь сами, а потом выложите Review...с опровержением или ещё с чем-то. Поясните Ваши слова, вызвавшие у меня недопонимание.
Общаться?-готов. Разъяснять что-то? Да, тоже готов. Но, не помогать в "опровержении".:)
Сейчас пришлю дополнительные материалы в личку.